值的解释以一种你期望的方式解释给你听
作者:Samuele Mazzanti
编译:ronghuaiyang
正文共:3096 字 13 图
英文原文: https://towardsdatascience.com/shap-explained-the-way-i-wish-someone-explained-it-to-me-ab81cc69ef30
导读: 上一篇文章 我们说到 SHAP 值可以用来对黑盒模型进行解释,具备比简单的逻辑回归更好的实际意义,那么 SHAP 值到底是什么?有什么实际意义?如何计算?
揭开神秘的面纱
在上次的文章中,我们看到 SHAP 值可以用来解释机器学习方法的决策。换句话说,我们使用 SHAP 来揭开黑箱模型的神秘面纱。
到目前为止,我们利用了 Python 的 SHAP 库,而没有过多考虑它是如何工作的。 足够讽刺的是,我们使用的 SHAP 本身就是一个黑盒!然而,理解 SHAP 值计算背后的思想对于理解它们的结果是至关重要的。
这就是为什么,在这篇文章中,我们将过一遍 Slundberg 和 Lee 在论文: https://arxiv.org/abs/1705.07874 中描述的 SHapley Additive exPlanations 的理论基础,并看看为什么 SHAP 值是按照他们计算的方式来计算的。
博弈论和机器学习
SHAP 值基于 Shapley 值,Shapley 值是博弈论中的一个概念。但博弈论至少需要两样东西:一个游戏和一些玩家。这如何应用于机器学习的可解释性?假设我们有一个预测模型,然后:
- “游戏”是复现模型的结果
- “玩家”是模型中包含的特征
Shapley 所做的是量化每个玩家对游戏的贡献。SHAP 所做的是量化每个特征对模型所做预测的贡献。
需要强调的是,我们所谓的“游戏”只涉及单一的观察样本。 一个游戏:一个观察样本。实际上,SHAP 是关于预测模型的局部可解释性的。
特征的 power set(幂集)
举个例子,我们可以想象一个机器学习模型(假设是线性回归,但也可以是其他任何机器学习算法),知道这个人的年龄、性别和工作,它可以预测一个人的收入。
Shapley 值是基于这样一种想法,即应该考虑每个玩家可能的组合的结果来决定单个玩家的重要性。在我们的例子中,这对应于 f 特征的每个可能组合( f 从 0 到 F, F 是所有可用特征的数量)。
在数学中,这被称为“power set”,可以用树表示。
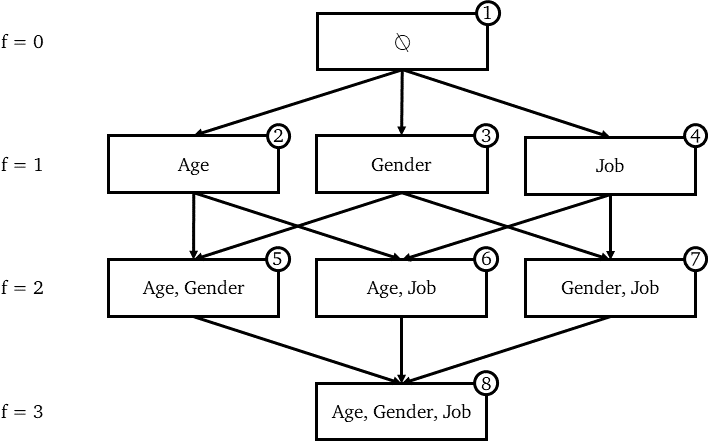
特征的Power set
每个节点代表一个特征组合,每条边代表包含一个在前一个组合中不存在的特征。
我们从数学上知道一个幂集的容量是 2^n^,其中 n 是原始集合的元素个数。实际上,在我们的例子中,我们有 2^F^ = 2^3^= 8 个可能的特征的组合。
现在, SHAP 需要为幂集中的每个不同的组合训练一个不同的预测模型,这意味着有 2^F^ 个模型。当然,这些模型在涉及到它们的超参数和训练数据时是完全等价的。唯一改变的是模型中包含的一组特征。
假设我们已经在相同的训练数据上训练了 8 个线性回归模型。我们可以用一个新的观察样本(我们称之为 x ₀),看看同样的 8 种不同的模型对这个观察样本的预测。
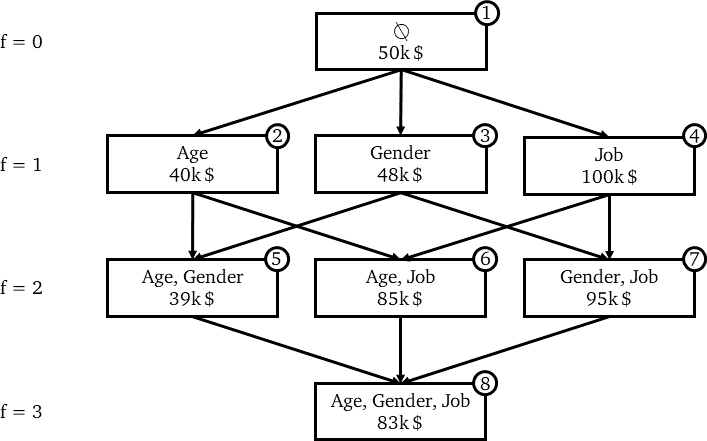
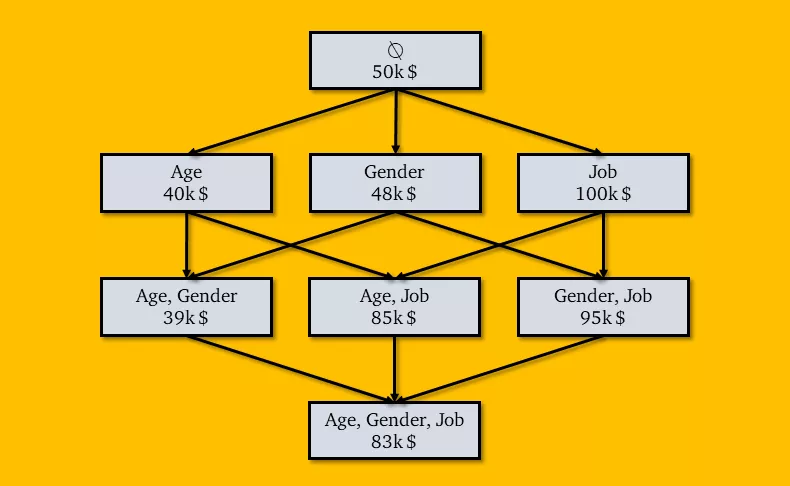
用不同模型预测 x ₀。在每个节点上,第一行表示特征的组合,第二行为 x ₀的模型预测收入。
这里, 每个节点代表一个模型。但是边代表什么呢?
构建 SHAP 公式(1/2) — 特征的边际贡献
正如上面所看到的,由一条边连接的两个节点只因为一个特征而不同,即底部的节点与上部的节点具有完全相同的特征,而上部的节点则没有。因此,两个连接节点的预测之间的差距可以归结为该附加特征的影响。这被称为特性的“边际贡献”**。
因此, 每条边代表一个特征对模型的边际贡献。假设我们在节点 1 中,节点 1 是一个没有任何特征的模型。该模型将简单地预测所有训练观察样本值的平均收入(50k 美元)。如果我们到了节点 2,这是一个模型只有一个特征(年龄),现在对 x ₀的预测为 40k 美元。这意味着知道 x ₀的年龄降低了我们的预测 10k 美元。
因此,年龄对只包含年龄作为特征的模型的边际贡献是-10k$。公式:
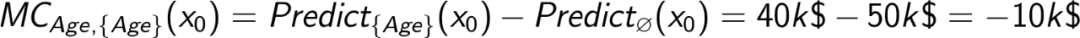
当然,获得年龄对最终模型的整体效果(即 x ₀的年龄的 SHAP 值),有必要考虑年龄在所有出现过模型的边际贡献。在我们的树表示中,这意味着要考虑连接两个节点的所有边:
- 上一个节点不包含年龄,且
- 下一个节点中包含年龄
在下面的图中,这些边已经用红色突出显示。
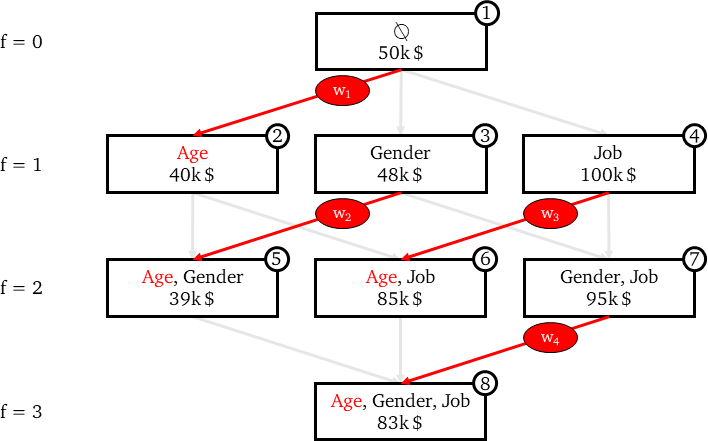
年龄的边际贡献
所有这些边际贡献然后通过加权平均数加以汇总。公式:
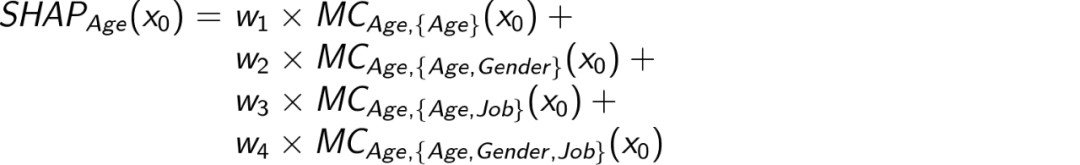
其中 w ₁+w ₂ +w ₃+w ₄ =1
构建 SHAP 公式(2/2) — 边际贡献的加权
我们如何确定边的权重(即 4 个模型中年龄的边际贡献)?
想法是:
- 所有边际贡献对具有 1 个特征的模型的权重之和应等于所有边际贡献对具有 2 个特征的模型的权重之和,以此类推……,换句话说,同一“行”上所有权值的和应该等于任意其他“行”上所有权值的和。在我们的例子中,这意味着: w ₁= w ₂+ w ₃= w ₄
- 对每个 f, f 个特征的模型的所有的边际贡献的权重应该是相等的。换句话说,同一“行”上的所有边应该相等。在我们的例子中,这意味着: w ₂ = w ₃
因此,(记住它们的和应该是 1):
- w ₁ = 1/3
- w ₂ = 1/6
- w ₃ = 1/6
- w ₄ = 1/3
看看上面的图,你能猜出一般框架中确定权重的模式吗?
剧透:边的权值是同一“行”中边总数的倒数。或者,同样地, f 个特征的模型的边际贡献的权重是可能的边际贡献的数量的倒数。
有计算这个的公式吗?其实很简单。
每个 f 个特征的模型都有 f 个边际贡献(每个特征一个),因此,计算可能的 f 个特征的模型的数量并将其乘以 f 就足够了。因此,问题归结为计算可能的具有 f 个特征的模型的数量,给定 f 并知道特征的总数是 F。这就是二项式系数的定义。
把所有的东西放在一起,我们得到了所有的具有 f 个特征的模型的所有边际贡献的数量,换句话说,每“行”的边的数量是:

取它的倒数就行了,我们就有了具有 f 个特征的模型边际贡献的权重。
如下图所示:
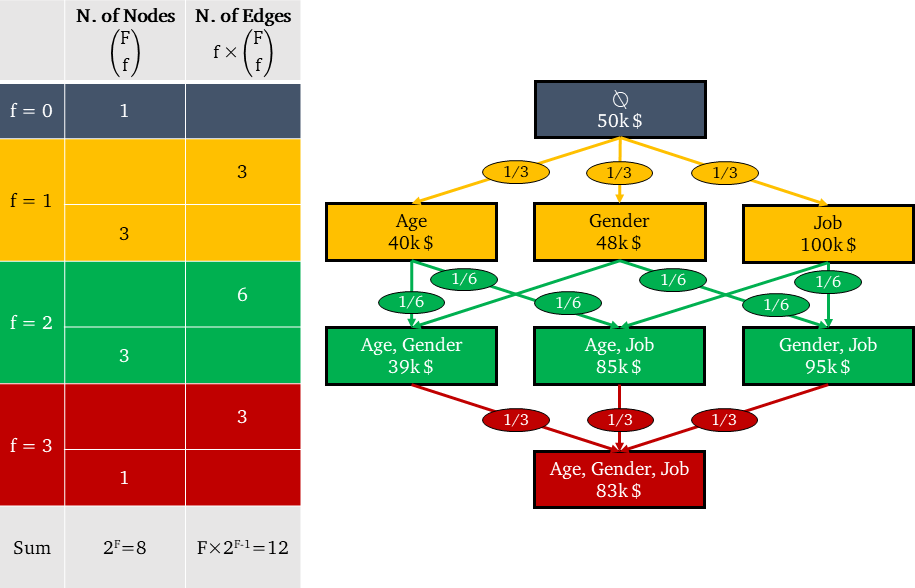
如何从边的数量中获得权重
现在,我们已经有了计算 x ₀ 的 Age 的 SHAP 值所需的所有元素:
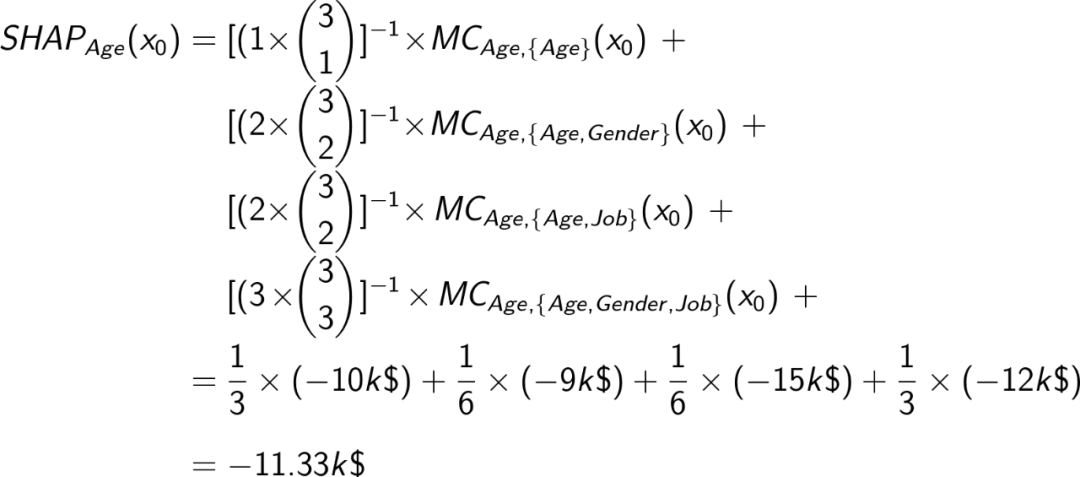
整理一下
我们建立了具有 3 个特征的模型来计算年龄的 SHAP 值。推广到任何特征和任何 F,我们得到了由 Slundberg 和 Lee 在文章中描述的公式:
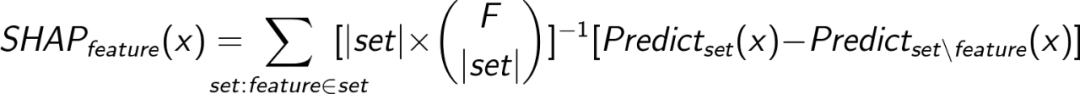
应用到我们的例子中,得到:
- SHAP_Age( x ₀) = -11.33k $
- SHAP_Gender( x ₀) = -2.33k $
- SHAP_Job( x ₀) = +46.66k $
把它们加起来就是 +33k,这正好�
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/%E4%BA%92%E8%81%94%E7%BD%91/%E5%80%BC%E7%9A%84%E8%A7%A3%E9%87%8A%E4%BB%A5%E4%B8%80%E7%A7%8D%E4%BD%A0%E6%9C%9F%E6%9C%9B%E7%9A%84%E6%96%B9%E5%BC%8F%E8%A7%A3%E9%87%8A%E7%BB%99%E4%BD%A0%E5%90%AC/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


