来源：新智元，编辑：数据派THU

本文介绍IML领域的历史，给出了最先进的可解释方法的概述，并讨论了遇到的挑战。

近年来，可解释机器学习（IML） 的相关研究蓬勃发展。尽管这个领域才刚刚起步，但是它在回归建模和基于规则的机器学习方面的相关工作却始于20世纪60年代。最近，arXiv上的一篇论文简要介绍了解释机器学习(IML)领域的历史，给出了最先进的可解释方法的概述，并讨论了遇到的挑战。

当机器学习模型用在产品、决策或者研究过程中的时候，“可解释性”通常是一个决定因素。

可解释机器学习（ Interpretable machine learning ，简称 IML） 可以用来来发现知识，调试、证明模型及其预测，以及控制和改进模型。

研究人员认为 IML的发展在某些情况下可以认为已经步入了一个新的阶段，但仍然存在一些挑战。

可解释机器学习（IML）简史

最近几年有很多关于可解释机器学习的相关研究， 但是从数据中学习可解释模型的历史由来已久。

线性回归早在19世纪初就已经被使用，从那以后又发展成各种各样的回归分析工具，例如，广义相加模型（generalized additive models）和弹性网络（elastic net）等。

这些统计模型背后的哲学意义通常是做出某些分布假设或限制模型的复杂性，并因此强加模型的内在可解释性。

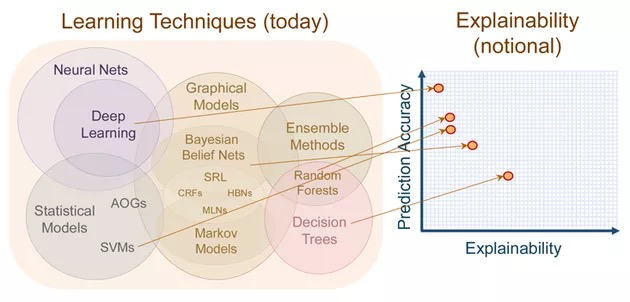
而在机器学习中，使用的建模方法略有不同。

机器学习算法通常遵循非线性，非参数方法，而不是预先限制模型的复杂性，在该方法中，模型的复杂性通过一个或多个超参数进行控制，并通过交叉验证进行选择。这种灵活性通常会导致难以解释的模型具有良好的预测性能。

虽然机器学习算法通常侧重于预测的性能，但关于机器学习的可解释性的工作已经存在了很多年。随机森林中内置的特征重要性度量是可解释机器学习的重要里程碑之一。

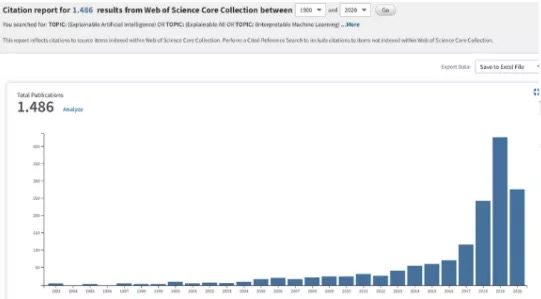
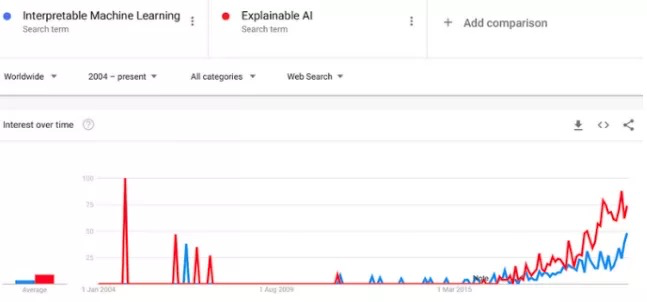
深度学习在经历了很长时间的发展后，终于在2010年的ImageNet中获胜。

从那以后的几年，根据Google上“可解释性机器学习”和“可解释的AI”这两个搜索词的出现频率，可以大概得出IML领域在2015年才真正起飞。

IML中的常见方法

通常会通过分析模型组件，模型敏感性或替代模型来区分IML方法。

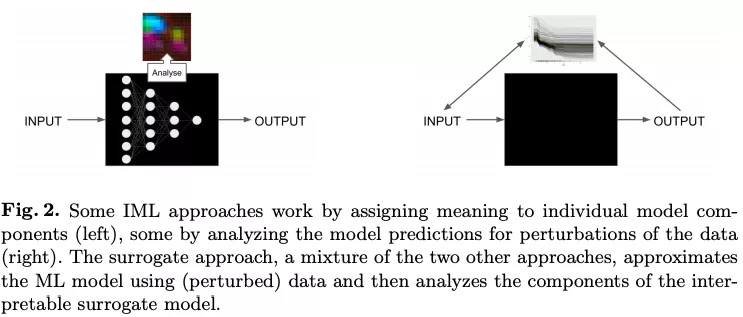
分析可解释模型的成分

为了分析模型的组成部分，需要将其分解为可以单独解释的部分。但是，并不一定需要用户完全了解该模型。

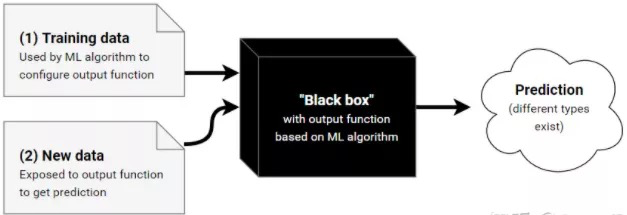
通常可解释模型是具有可学习的结构和参数的模型，可以为其分配特定的解释。在这种情况下，线性回归模型，决策树和决策规则被认为是可解释的。

线性回归模型可以通过分析组件来解释：模型结构（特征的加权求和）允许将权重解释为特征对预测的影响。

分析更复杂模型的成分

研究人员还会分析更复杂的黑盒模型的组成部分。例如，可以通过查找或生成激活的CNN特征图的图像来可视化卷积神经网络（CNN）学习的抽象特征。

对于随机森林，通过树的最小深度分布和基尼系数来分析随机森林中的树，可以用来量化特征的重要性。

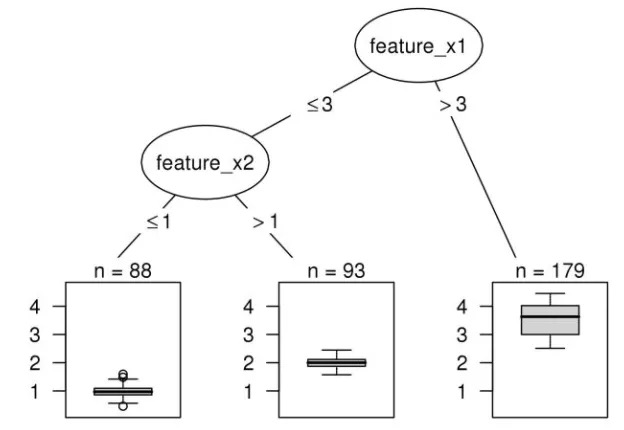
**模型成分分析是一个不错的工具，但是它的缺点是与特定的模型相关， 而且它不能与常用的模型选择方法很好地结合，通常是通过机器学习