同城搜索引擎中相似字符串查找那些事儿

来源： 58技术 丁斌

导读

本文主要介绍如何基于Levenshtein和Damerau Levenshtein自动机技术高效地解决在搜索引擎系统中相似字符串快速查找问题的技术原理和操作实践。文中创造性地提出一种Damerau Levenshtein自动机的有效构建算法，并创造性地给出了利用Levenshtein自动机和Damerau Levenshtein自动机技术，解决快速查找相似字符串问题实现方案的正确性理论依据论证。

背景

首先从字符串相似查找谈起。相似字符串查找，顾名思义即查询与目标字符串在物理上词形相似的字符串集合，在搜索引擎中有很多应用。其中比较常见的有2个：模糊搜索 (Fuzzy Search)和 拼写纠错(Spelling Check或Spelling Correction)。

• 模糊搜索

模糊搜索，或者叫做模糊查询，在搜索引擎中一般指在用户搜索意图不明确时，搜索引擎将用户的查询（query）与待检索的内容（doc）进行模糊匹配，找出与查询相关的内容。例如，查询名字Smith时，模糊查询方式就会找出与之相似的Smithe， Smythe， Smyth， Smitt等。这在克服少无结果搜索时尤其有用。注意本文讨论的模糊搜索特指查询query与待检索内容在文本字符串物理词形上的相似为目标，语义相似的模糊查询不在本文讨论范围内。

• 拼写错误

拼写纠错，或者叫拼写检查功能在搜索引擎中一般指的是：用户将查询的关键词提交给搜索引擎之后，搜索引擎便开始分析用户的输入，检查用户的拼写是否有错误，如果有的话，给出正确的拼写建议。例如用户在搜索引擎检索框中输入faeebook， 搜索引擎能给出拼写纠错建议facebook等。

搜索引擎中解决模糊搜索和拼写纠错本质上都是字符串文本相似匹配和度量问题。用户给搜索引擎输入了查询query字符串a,如何在待检索内容全集中遍历每一个字符串b，并迅速确定a和b是否相似，最终把所有与字符串a最相似的topN个字符串集合作为目标返回供进一步扩展召回或作为纠错建议的基础就成为解决问题的关键。

• 编辑距离

如何量化两个字符串之间的相似程度呢？有一个非常著名的量化方法，那就是编辑距离（Edit Distance）。

编辑距离指的就是，将一个字符串转化成另一个字符串，需要的最少编辑操作次数（比如增加一个字符、删除一个字符、替换一个字符）。编辑距离越大，说明两个字符串的相似程度越小；相反，编辑距离就越小，说明两个字符串的相似程度越大。对于两个完全相同的字符串来说，编辑距离就是 0。

编辑距离有多种不同的计算方式，比较著名的有莱文斯坦距离（Levenshtein distance）和最长公共子串长度（Longest common substring length）。其中，莱文斯坦距离允许增加、删除、替换字符这三个编辑操作，最长公共子串长度只允许增加、删除字符这两个编辑操作。

一些主流搜索引擎如著名开源搜索引擎Elastic Search都采用莱文斯坦距离（Levenshtein distance），同时包含更进一步的Damerau Levenshtein距离来度量字符串相似程度，以此为搜索引擎中的模糊搜索和拼写纠错提供基础解决方案。

由此引入本文将重点讨论的主题：Levenshtein和Damerau Levenshtein 自动机技术在58同城搜索引擎场景下的应用实践。在进入下一节之前，先用简短的篇幅迅速描述一下Levenshtein距离和Damerau Levenshtein距离的定义。

• Levenshtein Distance 和 Damerau Levenshtein Distance 定义

注意:为了简化表述，本文以下都非正式地将Levenshtein Distance简称为LD，将Damerau Levenshtein Distance简称为DLD。

Levenshtein Distance，参考维基百科上Levenshtein Distance （来自参考文献1）给出的定义如下：

维基百科对Damerau Levenshtein Distance（来自参考文献2） 给出的定义如下：

通过维基百科上关于Levenshtein Distance和Damerau Levenshtein Distance的描述可知DLD与LD的区别仅在于：如果字符串a和b的某处前后两个相邻字符前后互换位置后相同时， LD认为是经过2次变化，编辑距离是2；然后DLD认为这是一次变化，编辑距离是1。

本文接下来将由浅入深地从如下3个层次依次讨论利用编辑距离LD或DLD解决搜索引擎中查找相似字符串问题的实践技术细节：

1. 单纯计算两个字符串间的编辑距离问题
2. 在搜索引擎场景中如何快速找出与目标字符串a最相似的前N个候选字符串集合问题
3. 构造正确有效的Levenshtein DFA和Damerau Levenshtein DFA 高效求解搜索引擎中查找相似字符串问题

基础问题

利用LD和DLD度量字符串相似程度，首先面临要解决一个基础问题：

问题：对于任意给定的2个字符串a和b，如何用快速的算法求解a和b的LD和DLD？

在理解了维基百科中关于LD和DLD的定义后，解决这个问题并不困难。可以分2个层面逐步深入理解这个问题。

第一个层面：最朴素的思路是采用蛮力法递归求解。一种Levenshtein Distance的Java实现代码示例如下：

public static int RecurLevenshteinDistance(String a, int lenA, String b, int lenB) {
    if (lenA == 0)
        return lenB;
    if (lenB == 0)
        return lenA;

    int cost = (a.charAt(lenA-1) == b.charAt(lenB-1) ? 0 : 1);

    int dist1 = RecurLevenshteinDistance(a, lenA - 1, b, lenB) + 1;
    int dist2 = RecurLevenshteinDistance(a, lenA, b, lenB - 1) + 1;
    int dist3 = RecurLevenshteinDistance(a, lenA - 1, b, lenB - 1) + cost;

    return Math.min(Math.min(dist1,dist2),dist3);
}

public static void main(String[] args) {
    String a = "kitten";
    String b = "sitting";
    int re = RecurLevenshteinDistance(a, a.length(), b, b.length());
    System.out.println(re);//输出：3
}

显然递归的蛮力法求解效率低下，因为有大量重复的计算过程，其时间复杂度可以被证明是指数级的，不可取。

第二个层面考虑：为避免递归带来的大量重复计算过程，很容易得出求解LD和DLD的最快算法就是自底向上迭代求解的动态规划算法。容易分析得出动态规划算法计算LD和DLD的时间复杂度都是O(m*n)。其中m和n分别是字符串a和b的长度。

动态规划实现也非常简单，下面给出一种Levenshtein Distance动态规划Java实现，仅供参考：

public static int LevenshteinDistance(String a, String b) {
    int[][] dist = new int[a.length()+1][b.length()+1];
    for (int i = 0; i <= a.length(); i++)
        dist[i][0] = i;
    for (int j = 0; j <= b.length(); j++)
        dist[0][j] = j;

    for (int j = 1; j <= b.length(); j++) {
        for (int i = 1; i <= a.length(); i++) {
            int cost = (a.charAt(i-1) == b.charAt(j-1) ? 0 : 1);
            int dist = Math.min(dist[i - 1][j] + 1, dist[i][j - 1] + 1);
            dist[i][j] = Math.min(dist, dist[i - 1][j - 1] + cost);
        }
    }
    return dist[a.length() - 1][b.length() - 1];
}

public static void main(String[] args) {
    String a = "kitten";
    String b = "sitting";
    int dist = LevenshteinDistance(a, b);
    System.out.println(dist); //输出：3
}

可以得出结论：单纯求解两个字符串的LD或DLD，动态规划解法的时间复杂度O(mn)就是最快解法了。然后我们要解决得是搜索引擎场景下的大规模模糊查询中频繁用到的相似字符串查找，有其特殊性。于是进入第二个层次考虑问题。

搜索场景

之所以强调在搜索引擎场景，因为该场景有其固定特点如下：

• 搜索引擎场景下查找相似字符串是存在一个数量确定的候选字符串集合，用以进行与目标字符串a的相似性判断筛选，该候选集合一般是搜索引擎倒排索引的term词典集合；并且该倒排term词典集合规模一般可能很大，比如千万或上亿规模；
• 搜索引擎场景下查找相似字符串操作的次数可能非常频繁，比如用户的每一个模糊查询请求都将引发一次倒排term词典集合的相似字符串查找筛选过程，几千甚至上万的qps，就意味着每秒就要发生几千甚至上万次查找相似字符串的操作；
• 在搜索引擎场景下，我们往往只关心与目标检索串非常相似，也即编辑距离非常小的情形。比如参考流行开源搜索引擎es的做法是只关心编辑距离<=2,即0或1或2三种编辑距离的候选词。因为在搜索引擎场景下，我们很难想象提供一个与用户输入的检索目标词很不相似或很不相关的结果给用户是明智的。

鉴于搜索引擎场景下查找相似字符串问题的以上特点，如何高效地解决问题：在搜索引擎场景中如何快速找出与目标字符串a最相似的前N个候选字符串集合 是否有一些更有效、更优秀的解决方案呢？下面展开分析：

首先一个最朴素直观的解法是：

遍历搜索引擎索引倒排term词典集合中的全部 term,对其任意一个倒排 term字符串b，都以动态规划方法计算b与目标字符串a的LD或DLD编辑距离值，最后取结果编辑距离值最大的前N个倒排 term输出即可。

这种朴素解法存在的缺陷很明显：

1. 依次遍历倒排term词典集合过程比较耗时

考虑到一般搜索引擎索引中倒排term词典集合规模通常很大，经常达到千万或上亿规模，而查询请求又可能很频繁，如果对每一次模糊查询请求，都要依次从头到尾遍历倒排term词典集合可能比较耗时。

于是很自然的优化目标是：能否做到不必遍历倒排term词典集合中的所有的term？换句话说，是不是能对这个大规模的倒排term字符串集合做个预处理，使其按照某种特定的内存布局预先存储好，比如类似trie树一类的tree数据结构，这样一来，遍历这样的tree类数据结构存储的大规模倒排term词典集合时，有可能在一些正确的理论指导下，可以避开tree类数据结构中的某些根本不需要遍历的分支，从而减少遍历term数量，以提高遍历效率。这个过程可以被形象地称为"减枝"。

经过调研我们发现：这个存储倒排term词典集合的类似trie树一类的数据结构，在流行开源搜索引擎es的内核实现组件lucene的较新的版本（lucene4以后）中已经有实现，叫做FST（Finite State Transducer）词典，是一种有限状态机，lucene 4中有java代码的开源实现。

FST有两个优点：1）空间占用小。通过对词典中单词前缀和后缀的重复利用，压缩了存储空间；2）查询速度快。O(len(str))的查询时间复杂度。

FST的原理和实现细节网络上能够轻松搜索得到，不是本文论述的重点。本文略过不表。

那么，现在问题演变为：

基于FST词典表达的倒排term表，该有怎么样的“剪枝”策略，以应对大规模连续判断每个term字符串b是否与给定的目标字符串a足够相似，即编辑距离LD或DLD足够小，比如小于预先设定好的阈值1或者2？

该问题的解决方案是提升搜索引擎中查找相似字符串效率的重要手段，是非常有价值的思路，限于篇幅本文暂时不讨论该主题，留待后续系列文章另行论述。

大规模计算每一个候选倒排term字符串b与目标字符串a的编辑距离比较耗时

如前文提到的，动态规划方法求解字符串a和b间的LD/DLD，时间复杂度是O(m*n).( m和n分别是a和b的长度)，因为动态规划要自底向上依次迭代计算a、b字符串的每一种前缀子串对组合间的编辑距离。这个过程在大规模遍历倒排词典集合每次都要计算时显得效率较低。怎么优化这个过程呢？

如前文所提到，考虑到在搜索引擎场景下，我们往往只关心与目标检索串非常相似，也即编辑距离非常小的情形（比如参考流行开源搜索引擎es的做法是只关心编辑距离<=2,即0或1或2三种编辑距离的候选词）的特点，于是把问题限定到：在只需要迭代筛选找出与目标词a编辑距离LD/DLD是0、1、2的所有候选词的前提下，如何快速大规模筛选相似的候选字符串呢?

显然，如果依然采用朴素的遍历倒排词典集合中每一个词b，都与目标词a用动态规划先求出编辑距离，然后判断是否<=2，如果是就保留否则就丢弃的做法，显然显得不那么明智。因为如果编辑距离大于2的字符串，其实是没有必要耗费O(m*n)的时间先计算编辑距离的，因为显然可以基于某种判断提前终止计算，因为这些编辑距离>2的候选字符串明显不那么相似。

于是解决问题思路演变为：

如何加速判断字符串a和b是否非常相似，即编辑距离LD或DLD是否<=2, 而不是缓慢地用动态规划去先计算编辑距离 再判断？

稍作调研就会发现：该问题解决方案很明确–引入自动机(Automaton),具体来说是引入确定有限状态自动机（deterministic finite automaton, DFA）。LD和DLD两种编辑距离对应两种不同的确定有限状态自动机(DFA）。这两种DFA实现差别比较大，难度差别也很大。具体来说Damerau Levenshtein DFA 实现复杂程度 远高于 Leveshtein DFA。

经过大量调研互联网或其他公开的资料途径，我们发现：

1）Leveshtein DFA的编程实现相对容易，可参考的实现过程也比较多。但理论论证Leveshtein DFA实现正确性的公开资料也及其匮乏，或者不够系统；

2）Damerau Levenshtein DFA的编程实现几乎没有，即使有一些不多的开源实现过程都是漏洞百出，正确性存疑。当然理论论证Damerau Leveshtein DFA实现过程正确性的公开文章资料亦是寥寥无几。

有鉴于此，于是正式引入本文要重点论述的主题，也是本文提出的技术创新点所在：

本文将创造性地提出Damerau Levenshtein DFA构建方法论和伪代码实现，并且以定理论证方式给出Leveshtein DFA和Damerau Levenshtein DFA构建和实现方法正确性的理论证明。

进阶

首先简单谈一下DFA（Deterministic Finite Automata，确定的有穷自动机）和自动机(Automaton)。

很多人一听到“自动机”就觉得很陌生高深难理解,莫名地恐惧自动机。很多计算机科班同学最早接触有限自动机可能是在本科课程《编译原理》中，后来可能又会在CLRS《算法导论》黑宝书中的《利用优先自动机进行字符串匹配》一节中接触到用有限自动机理论解决字符串匹配以及改进版的KMP算法等内容。因此在进入正题之前，本文先来迅速补充一下关于有限自动机的相关知识，尽力熟悉一下有穷自动机解决问题的本质，消除自动机恐惧症。

4.1 熟悉自动机和DFA

1. 有限自动机FA(Finite Automata)

   我们一般提到的自动机都是指有限自动机（或者叫有穷自动机）。

   在计算机科学中有穷自动机分为DFA和NFA：

   • 确定的FA (Deterministic finite automata, DFA)

   • 非确定的FA (Nondeterministic finite automata, NFA)

     有穷自动机 ( Finite Automata，FA )由两位神经物理学家MeCuloch和Pitts于1948年首先提出，是对一类处理系统建立的数学模型

这类系统具有一系列离散的输入输出信息和有穷数目的内部状态（状态：概括了对过去输入信息处理的状况）

系统只需要根据当前所处的状态和当前面临的输入信息就可以决定系统的后继行为。每当系统处理了当前的输入后，系统的内部状态也将发生改变

2.确定的有穷自动机DFA(Deterministic Finite Automata)

M = ( S，Σ ，δ，s0，F )* S：有穷状态集

• Σ：输入字母表，即输入符号集合。假设ε不是 Σ中的元素

• δ：将S×Σ映射到S的转换函数。s∈S, a∈Σ, δ(s,a)表示从状态s出发，沿着标记为a的边所能到达的状态。

• s0：开始状态 (或初始状态)，s0∈S

• F：接收状态（或终止状态）集合，F⊆ S

  例如下图所展示的一个DFA

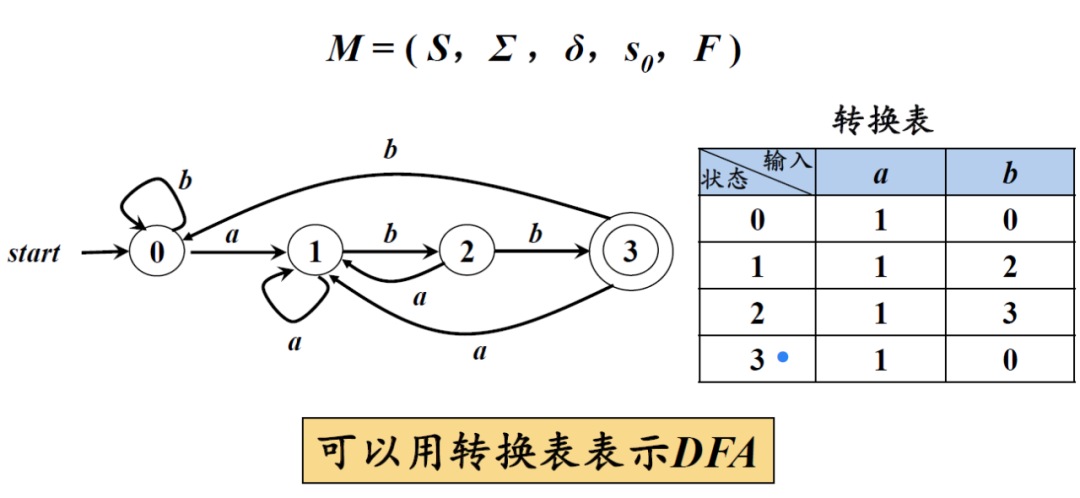
1. 非确定的有穷自动机NFA(NonDeterministic Finite Automata)

   M = ( S，Σ ，δ，s0，F )

   例如下图所展示的一个NFA

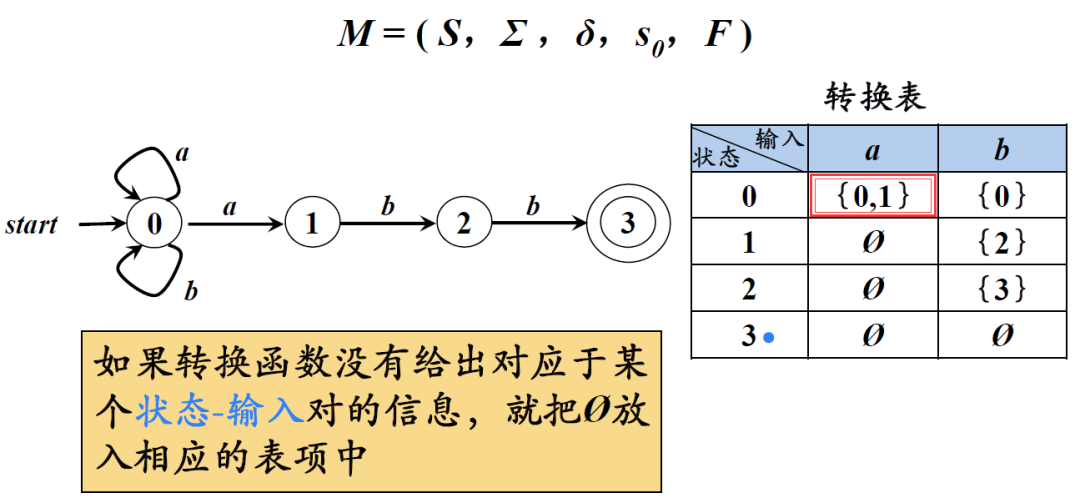
• S：有穷状态集
• Σ：输入符号集合，即输入字母表。假设ε 不是Σ中的元素
• δ：将S×Σ映射到2S的转换函数。s∈S, a∈Σ, δ(s,a)表示从状态s出发，沿着标记为a的边所能到达的状态集合
• s0：开始状态 (或初始状态)，s0∈S
• F：接收状态（或终止状态）集合，F⊆ S

注意：DFA与NFA的区别在于，DFA对于每一次输入只能产生唯一一个结果，结果是确定的。而NFA的一次输入可能产生多个结果。如上图用红色方框标出的位置，DFA的每一次输入只对应一个结果，而NFA的依次输入可能对应多个结果，形成一个结果集。

综合以上：我们不妨尝试高度抽象且不失直观感性地总结一下有穷自动机，尤其是DFA解决问题的思路：

有穷状态自动机解决问题的思路，本质上就是: 在预处理阶段我们生成一个包含: 要素1）一系列抽象出来的状态集合S，（当然S里包含初始状态s0和可以被接受的状态的集合F,这二者能够被确定）；要素2）一个包含所有可能输入符号的输入符号集合Σ；和要素3）对于任意属于状态集合S的任意元素s, 以及属于输入符号集合Σ的任意符号c，能够明确转换生成新状态的状态转换函数 δ(s,c) 。

当具备了这三要素后，就可以在后续大量判别过程中，从头到尾依次迭代给定的每个输入符号序列，比如给定的目标字符串a, 然后不断地 转化生成新的状态 ，并且同步判断每一步产生的新状态是否可被接受，直到输入符号序列迭代结束。通过这样的方式 一般能在线性时间甚至更快的时间复杂度内快速解决问题。

后面我们也将通过构造Levenshtein DFA或 Damerau Levenshtein DFA解决字符串相似性判断问题来加深对上面这段话的理解。

接下来我们给出一些将DFA应用于搜索引擎中查找相似字符串的直观理解。

4.2 DFA应用于搜索引擎中查找相似字符串的直观理解

首先我们再重新审视一下我们的待解决目标问题：

• 如何快速确定某个字符串b与目标字符串a是否最相似，即编辑距离LD或DLD<=2？

前文已经提到，单纯用动态规划法先计算a和b的LD/DLD，再判断是否<=2，时间复杂度是O（length[a] * length[b])，在大规模判断中每次都这样操作太慢。

引入DFA优化这一过程的思想在于：提前对目标字符串a进行预处理，生成一个DFA，该DFA的核心要素包括：

• 所有可能的有限的状态集合S,初始状态S0，能被接受的所有状态集合F；
• 输入符号集合Σ ：表明所有可能输入的符合的集合；
• 状态转换函数δ：Convert(State s, Char c) -> newState

有了DFA以后，确定某个字符串b与目标字符串a的最相似问题，就可以按如下伪代码示例进行操作：

PRE-PROCESS(a)            //预处理生成目标字符串a对应的dfa结构
1 dfa <- a

CHECK-SIMILAR-STRINGS (dfa,b) //判断b是否与a相似
1 s0 <- dfa.initState()
2 s  <- s0                   //以dfa的初始状态S0初始化状态s
3 n  <- length[b]
4 for i <- 1 to n            //依次遍历待判断字符串b的每个字符c
5     do c <- b[i]
6        s <-dfa.Convert(s,c)
7        if null == s         //无状态，返回false,提前终止流程
8           then return false
9           else if dfa.IsAccept(s)
10                  then return true //字符c被接受，完成判断
11                  else continue

简单看一下上述伪代码示例过程的执行时间复杂度：

• 预处理过程生成目标字符串a的dfa，时间复杂度是O(length[a]) 。后文我们会详细分析该过程的时间复杂度。
• 第6行dfa状态转化过程耗费常量时间。因为dfa内部的所有States都被提前缓存好了，转化过程只是一个逻辑判断过程而已。
• 第4~11行迭代遍历待check字符串b，可能在第8行或者第10行提前终止迭代过程，因此最大迭代length[b]次，因此每次判断时间复杂度是O(length[b])。

可见：引入DFA后，增加了预处理过程O(length[a])的时间复杂度，每次相似性判断的时间复杂度从动态规划算法的O（length[a] x length[b])降低至O(length[b])。该过程的前提是正确构造出正确高效的DFA结构。 我们接下来论述该主题。

4.3 Levenshtein DFA

4.3.1 分析 Levenshtein DFA

通过前文4.1节我们已知一个DFA有5要素组成：M = ( S，Σ ，δ，s0，F )，5要素可以归结为3类要素如下：

• 状态：跟状态有关的要素有3个分别是：S是状态集合，s0是初始状态，F是接受状态集合；
• 转换函数：而δ是定义在S和Σ上的转换函数，能生成一个新的状态。
• \\ 输入符号：\\ 此外Σ 是输入符号集合；

那么Levenshtein DFA中这5个要素该如何定义呢？怎么直观感性理解呢？

本质上来看，我们是要对目标字符串a预处理以构造编辑距离LD<=最大编辑距离maxEdit(2或1)的DFA，下面我们以目标字符串a为“woof",编辑距离LD <=1为例来说明Levenshtein DFA的构造过程。

首先我们直观思索一下Levenshtein DFA的状态应该是什么结构或怎么定义能满足我们解决问题的诉求，我们的诉求是：对任意给定的字符串b,比如wof，判断b和目标字符串a，即 wof 和 woof 的LD编辑距离是否满足<=1的条件。按照前文提到的动态规划法自底向上解决问题的思路，我们可能的做法应该是：

1. 依次迭代列出b串和a串的所有前缀子串。

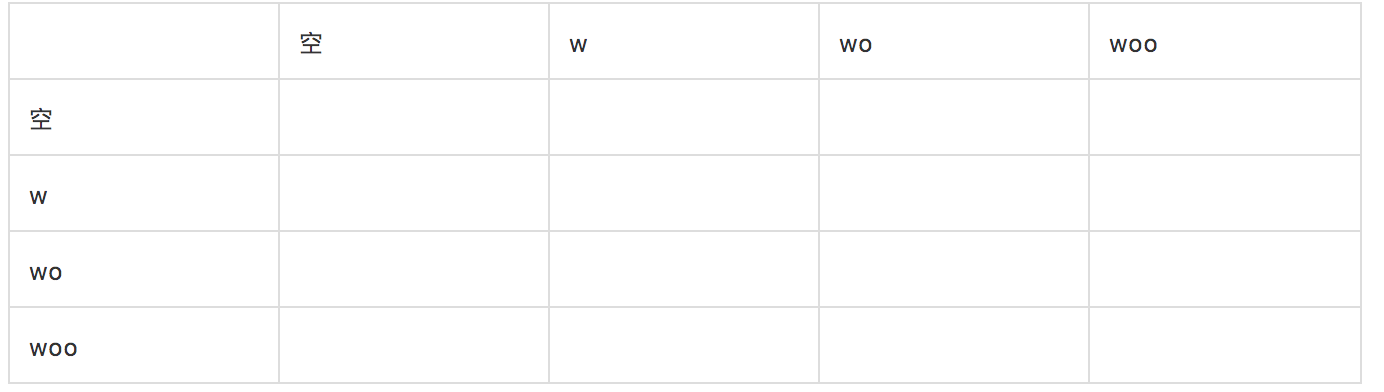
如上方表格示意，第一行为目标字符串a自底向上的每一个前缀子串,第一列为待检查字符串b自底向上的每一个前缀子串。（注意空串也是前缀子串,不能省略，因为动态规划方法自底向上解决问题的一个重要基础就是空，空串或空集合）。

1. 自底向上迭代求出每一个前缀子串组合见的编辑距离。

如下面伪代码所示：

#a是目标字符串，b是待判断字符串
for i <- 0 to length[b]
    do for j <- 0 to length[a]
           do 计算b[..i] 与 a[..j] 前缀子串间的 编辑距离dist[i,j]
              #而 dist[i,j] 跟dist[i-1,j],dist[i,j-1],dist[i-1,j-1]以及a[i]和b[j]是否相等有关系

既然dist[i,j] 跟dist[i-1,j],dist[i,j-1],dist[i-1,j-1]以及a[i]和b[j]是否相等有关系，那么我们是不是就可以定义任意待判断字符串b的每一个前缀子串（假定名称为 prev-substr(b) ) 与目标串a的 所有前缀子串集合中每一个元素的 编辑距离值 的集合呢。对应到上面表格中的例子，所有的状态应该就是每一行的元素值的集合。全部状态集合S是（计算过程如下表格）：

{
  { 0,1,2,3,4 },
  { 1,0,1,2,3 },
  { 2,1,0,1,2 },
  { 3,2,1,1,1 }
}

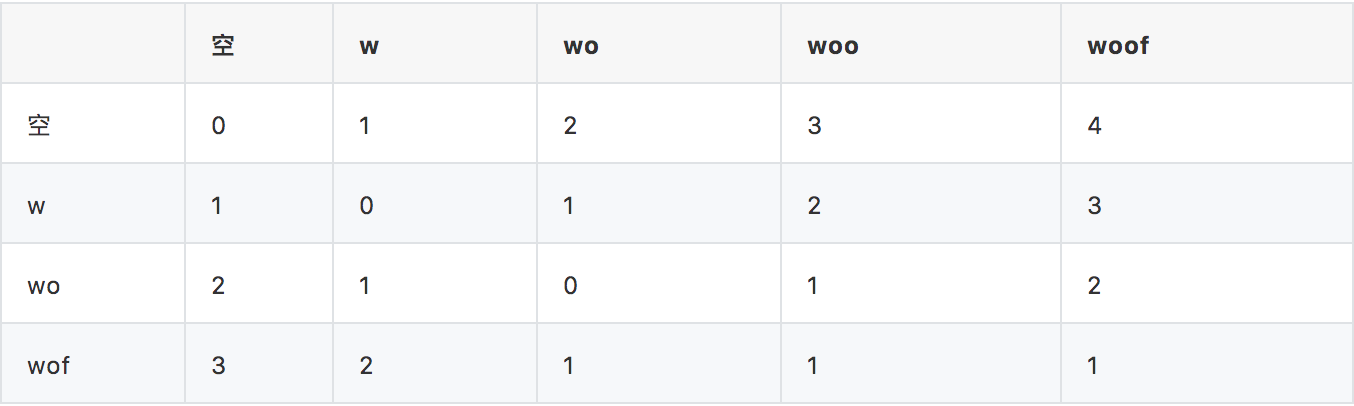
因此结论是：Levenshtein DFA的状态可定义为：任意待判断字符串与目标字符串a的依序前缀子串间编辑距离值的集合。

初始状态s0 应该就是prev-substr(b) 前缀子串为空时的状态，即 { 0,1,2,3,4 }。推而广之，对于目标字符串a ,初始状态s0应为：{0,1,2,…,length[a]}。 于是形成计算初始状态函数 Start 伪代码如下：

Start(String a )
1   n <- length[a]
2   State s = {0,1,...,n}
3   return s

考虑到我们问题的目标是要检查判断出来b与目标字符串a编辑距离LD值是否<=1 ，因此 接受状态就应该是 每个状态最后一个值<=1的所有状态的集合。对应于本例，接受状态结合F只有一个元素，即：F = { { 3,2,1,1,1 } }。当然，如果我们要解决的是检查判断出来b与目标字符串a编辑距离LD值是否<=2， 那么接受状态集合就是：{ { 2,1,0,1,2 } ，{ 3,2,1,1,1 } }。这是就2个或更多的元素。至此，Levenshtein DFA 中状态类3个要素 状态集合S，初始状态S0，可接受状态集合F 都能容易直观理解了。再抽象一下可得出结论：

对于目标字符串a,最大编辑距离LD阈值为maxEdit的相似性判断问题中， 状态s= {s0,s1,…sn} （n= length[a]）是否可以被接受的条件是：sn <= maxEdit。 于是形成 判断状态s是否可被接受函数IsMatch:

IsMatch(State s, maxEdit)
1   n <- length[s]
2   return s[n-1] <= maxEdit

对于状态s的任意一个编辑距离值 v, 这里在做一下扩展，给出定理1。

定理1：在构造目标字符串a,最大编辑距离阈值为maxEdit 的Levenshtein DFA时，对于任意状态s = {s0,s1,…,sk sn}中任意k满足0<= k <=n，如果s[k] > maxEdit，则可以用新状态snew = {s0,…,s[k-1], maxEdit +1, s[k+1],…,sn} 代替状态s。

定理1基于这样的理解：不管任意编辑距离值v > maxEdit的v值具体是多大，其对相似性结果判断的效果是等价的。因此可以全部以maxEdit +1 来表示所有 v > maxEdit 的v值。 这样做的好处是 利于极大减少 Levenshtein DFA中全部状态集合S的规模，降低内存，也能节省处理时间。这一点非常重要。 定理1的证明过程略。

根据定理1，上述例子目标字符串a = ’woof’, maxEdit = 1，待判断字符串b = ‘wof’ 的全部状态集合演变为：

状态集合S由
{
  { 0,1,2,3,4 },
  { 1,0,1,2,3 },
  { 2,1,0,1,2 },
  { 3,2,1,1,1 }
}
演变为：
{
  { 0,1,2,2,2 },
  { 1,0,1,2,2 },
  { 2,1,0,1,2 },
  { 2,2,1,1,1 }
}

基于对Levenshtein DFA 中状态值可以定义为 编辑距离LD值的集合的认识, 再参考第1节中提到的维基百科中对LD的定义，借助动态规划方法思想，容易写出在上一个状态s前提下，Levenshtein DFA 处理新读入任何字符c 生成新状态的“步进函数”Step 伪代码。（Step函数作用为：在上一个状态基础上，读入一个新字符，转换到下一个状态)

Step(String a,  State s,  Char c)
 1   State snew = [s[0] + 1 ]
 2   for i <- 1 to length[a]
 3       do  cost = (a[i-1] == c ? 0 : 1)
 4           dist = Min(s[i-1] + cost, s[i] + 1, snew[i-1] +1 )
 5           snew.append(Min(dist, maxEdit+1))//根据定理1，maxEdit+1能代表所有无效的编辑距离值
 6   return snew

再来看一下 另外2个要素：状态转换函数 δ和输入符号集合Σ 。

• 状态转换函数 δ

Levenshtein DFA 的状态转换函数 δ 其实比较简单，只需要把构造Levenshtein DFA过程的每一个状态的过程缓存成为哈希表结构如：HashMap<State, HashMap<char, State> >存储于内存中，表明了任意State经过任意字符char 能转化成的唯一状态State的逻辑。对于任意State对应的HashMap<char,State>中没有的char 都是不能产生有效相似性判断结果的，因此都被省略了。这也是应用Levenshtein DFA解决字符串相似性判断问题时能提高性能的一个影响方面。

• 输入符号集合Σ

显然我们要解决的问题是面向所有可能的字符串，那么每次输入给自动机判断的就是任意字符，自然地，输入符号集合就是所有字符集合，即字母表。虽然取字母表集合作为Levenshtein DFA或Damerau Levenshtein DFA的输入字符集合没有错，但稍作分析会发现有进一步更有效的处理办法。下面我们以先给出定理论述，再给出定理证明的方式依次论述 Levenshtein DFA 输入符号集合Σ的优化策略:

定理2：在构造目标字符串a的Levenshtein DFA时，已知：

1）Set(a) 为 目标字符串a的所有包含的字符的集合;

2）字符c1,c2 为任意两个不属于Set(a)的字符,即 c1 ∉ Set(a) 且 c2 ∉ Set(a)，且满足c1 != c2；

3）δ(s,c) 为状态转换函数；

对于任意前一个状态s，令 s1 = δ(s,c1) , s2 = δ(s,c2) 分别为输入c1和c2后转换所得的新状态，则 s1 必定恒等于s2。

先来直观理解一下定理2：假设目标字符串 a = woof， 则Set(a)为 { ‘w’, ‘o’, ‘o’, ‘f’ }, 因为 c1 ∉ Set(a) 且 c2 ∉ Set(a) 且 c1 != c2，假设c1=‘x’,c2=‘y’, s1 = δ(s,’x’) 和 s2 = δ(s,‘y’)，那么状态s1和s2必定相等。是这样吗？肯定。因为s1和s2的状态不过是Levenshtein Distance编辑距离值的集合而已，根据LD编辑距离的定义，在给定的相同目标字符串a和相同的前一个状态s前提下，下一个状态仅仅与新读入字符c与目标字符串a中对应位置字符a[k]是否相等有关系，如果新读入的2个字符都与目标字符串a中对应位置字符a[k]相等或不相等，则根据LD定义，下一个编辑距离值LD必定相等。

下面给出定理2证明过程：

证明：

已知: a是目标字符串，n = length[a];

Set(a) 为 目标字符串a的所有包含的字符集合;

任意2个字符：c1和c2满足 c1 ∉ Set(a) 且 c2 ∉ Set(a) 且 c1 != c2;

δ(s,c) 为状态转换函数;

s1 = δ(s,c1) , s2 = δ(s,c2);

令: 任意上一个状态值 s = {s0,s1…sn};

根据dfa构造过程的直观理解，假设s 是任意待判断字符串b的任意前缀子串b[0…k]与目标字符串a的DL值集合,其中k∈[0,n]，

则：根据LD定义和动态规划方法，通过前文论述过的Step()步进函数可得出求解s1状态的伪代码如下：

Step(String a,  State s,  Char c1)
 1   State s1 = [s[0] + 1]
 2   for i <- 1 to length[a]
 3       do  cost = (a[i-1] == c1 ? 0 : 1)
 4           dist = Min(s[i-1] + cost, s[i] + 1, s1[i-1] +1 )
 5           s1.append( Min(dist, maxEdit+1) )
 6   return s1

求解s2状态的伪代码如下：

Step(String a,  State s,  Char c2)
 1   State s2 = [s[0] + 1]
 2   for i <- 1 to length[a]
 3       do  cost = (a[i-1] == c2 ? 0 : 1)
 4           dist = Min(s[i-1] + cost, s[i] + 1, s2[i-1] +1 )
 5           s2.append( Min(dist, maxEdit+1) )
 6   return s2

又因为c1和c2是满足 c1 != c2 且 c1 ∉ Set(a) 且 c2 ∉ Set(a)的任意两个字符。那么上述伪代码中第3行计算出的cost 必定都等于0。于是迭代完全部过程后，s1 必定恒等于s2。证明完毕。

定理3：在构造目标字符串a的Levenshtein DFA时，已知：

1）Set(a) 为 目标字符串a的所有包含的字符的集合;

2）字符c0 为任意一个不属于Set(a)的字符，c0 ∉ Set(a)；

则目标字符串a的Levenshtein DFA的输入符号集合Σ可配置为: {Set(a), c0}。

首先我们仍然来直观理解一下定理3: 首先根据前文的分析我们已经知道Levenshtein DFA的输入符号集合Σ为全体字符集合，或者叫做字符表集合Alpha。字母表集合可以表达为Set(a）和Set(a)补集的并集。现在定理2本质上是用了Set(a)的补集中的任意一个元素组成的单元素集合代替了Set(a)的补集。而根据定理1我们知道，Set(a)的补集中任意一个元素经过转换函数生成的新状态都是相等的。于是定理3 就容易理解了。

下面给出定理3证明过程：

证明：

已知: a是目标字符串，n = length[a];

Set(a) 为 目标字符串a的所有包含的字符集合;

字符c0 为任意一个不属于Set(a)的字符，c0 ∉ Set(a)；

s1 = δ(s,c1) , s2 = δ(s,c2);

令: c1 ∉ Set(a) 且 c2 ∉ Set(a) 且 c1 != c2 是不属于Set(a)的任意两个字符，则：根据定理1，得到 c1 和c2 经过dfa的转换函数会生成两个相等的新状态，即：同一个DFA 状态值。因此c1和c2对Levenshtein DFA状态转化贡献完全一致。可以简化表达只取其中任意一个字符加入到 Levenshtein DFA的输入符号集合Σ。推而广之， Set(a) 补集中任意元素对 Levenshtein DFA 作用等价，因此只取Set(a) 补集中任意字符元素c0加入输入符号集合Σ即可代表整体Set(a) 补集集合对 Levenshtein DFA的作用。因此 目标字符串a的Levenshtein DFA的输入符号集合Σ可配置为: {Set(a), c0}。证明完毕。

于是，根据定理3，我们可以写出 求解 输入符号集合Σ的函数Transitions()的伪代码如下：

Transitions(String a)
1   Set(a) <- a所有包含的字符组成的集合
2   c0     <- 为任意 不属于Set(a)的抽象字符
3   return { Set(a), c0}

定理4：在构造目标字符串a的Levenshtein DFA时，已知：

1）Set(a) 为 目标字符串a的所有包含的字符经过去重后的集合;

2）字符c0 为任意一个不属于Set(a)的字符，c0 ∉ Set(a)；

则目标字符串a的Levenshtein DFA的输入符号集合Σ可配置为: {Set(a), c0 }。

定理4证明：

已知: a是目标字符串，n = length[a];

Set(a) 为 目标字符串a的所有包含的字符集合;

字符c1,c2是任意两个属于Set(a)的字符，且c1 == c2；

则：根据定理2的证明过程克制，转换函数经过c1与c2生成的新状态必相等，即：同一个DFA 状态值。因此c1和c2对Levenshtein DFA状态转化贡献完全一致。可以简化表达只取其中任意一个字符加入到 Levenshtein DFA的输入符号集合Σ。再结合定理3，可得定理4得证。

证明完毕#。

根据定理4，求解 输入符号集合Σ的函数Transitions()继续演变为：

Transitions(String a)
1   Set(a) <- a所有包含的字符组成的集合
2   Set(a) <- Set(a).RemoveDuplicate()   #元素去重
3   c0     <- 为任意 不属于Set(a)的抽象字符
4   return { Set(a), c0}

定理5：在构造目标字符串a的Levenshtein DFA时，已知：

1）s = {s0,s1, …, sn} 为任意上一个状态，其中n = length[a]，(注意length[s] = n + 1);

2）maxEdit 为相似性判断条件中预设的最大编辑距离阈值；

3）δ(s,c) 为状态转换函数；

则 对于任意k 满足 0<= k <= n-1 且 s[k] > maxEdit ，则 求解基于上一个状态s的输入符号集合Σ过程中必然可以不考虑k位置的字符a[k] 。

首先我们直接给出根据定理5演变的求解 输入符号集合Σ的函数Transitions()的伪代码如下：

注意，根据定理5,Transtions()函数的前提条件又多了2个，即：任意上一个状态s 和 最大编辑距离：maxEdit。

Transitions(String a, State s, int maxEdit)
1    n <-length[a]
2    resultChars = {}    #结果字符集合，初始化为空集
3    for i <- 0 to n-1
4        do if s[i] <= maxEdit
5              then resultChars.Append(a[i])
6    resultChars <-  resultChars.RemoveDuplicate()   #集合去重
7    c0     <- 为任意 不属于resultChars 的抽象字符
8    resultChars.Append(c0)
9    return resultChars

注意：一些网络上公开的介绍的Levenshtein DFA构造的文章，比如其中一篇比较流行的文章< < Levenshtein automata can be simple and fast > > （来自参考文献3）中给出的解释是如下图截图红色框中所示：

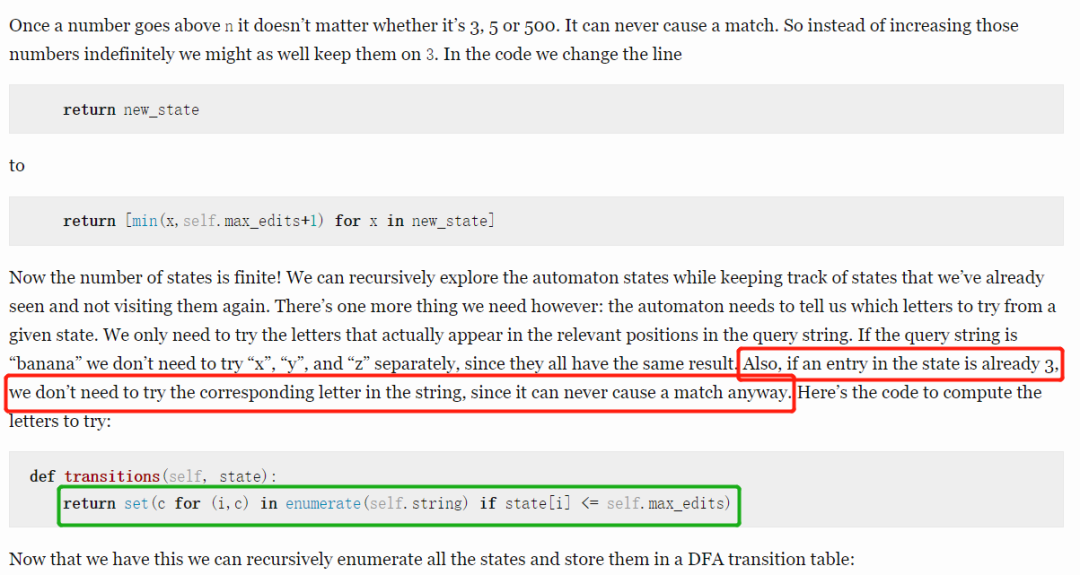
该文作者认为：如果某一个位置出现了状态值3，也就是编辑距离值3，（作者说这句话的上下文是最大编辑距离阈值maxEdit是2），我们就不需要再去尝试目标字符串中相应位置的字符了，原因是它从此再也不会导致一个满足最终编辑距离<=maxEdit的相似匹配了。事实真是如此吗？本文作者经过充分深入的思考，最终发现该文章中此处的解释其实是错误的。为什么呢？接下来将给出一个反例以证明该文中解释是错误的，如下：

假定要构造目标字符串a = ‘abc’, Levenshtein Distance 编辑距离阈值为1的Levenshtein DFA，构造过程可如下表格演示：

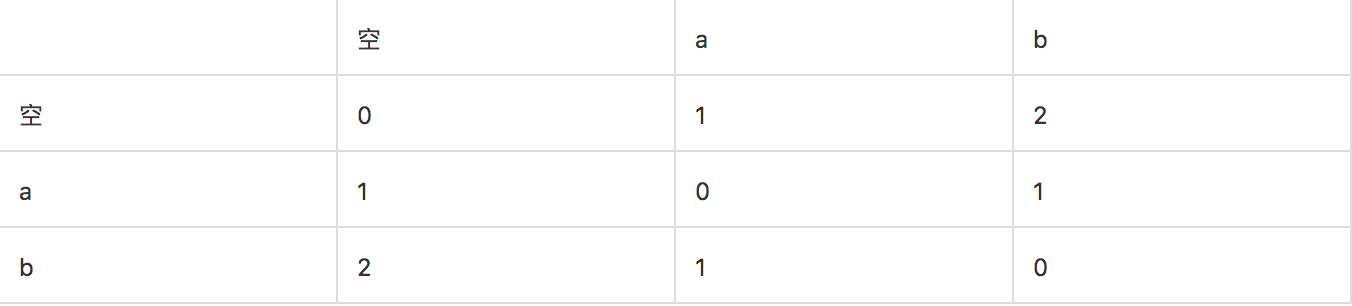
第一行为目标字符串a, 第一列依次为假定遇到的输入符号，先是字符‘a’,再是字符’b’。可以看到当依次读入了字符’a’和’b’以后，状态转化为 s = {2,1,0,1}。此时对照定理4的内容，s[0] = 2 > maxEdit (本例子中maxEdit 为1)，位置是0。于是 目标字符串a的第0号位置的字符a[0] = ‘a’就不用被纳入考虑 基于上一个状态s = {2,1,0,1}的Step函数步进过程去计算新的状态，为什么呢？如果按照上面改文章的解释，因为这个位置的字符a[0] = ‘a’不会再导致一个满足最终编辑距离<=maxEdit为1的相似匹配了。是这样吗？我们如下表格验证一下：

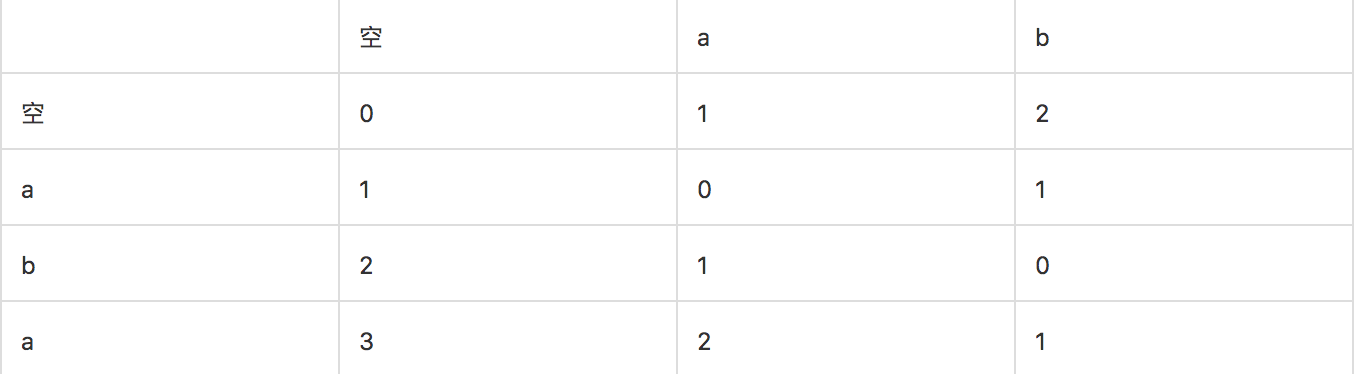
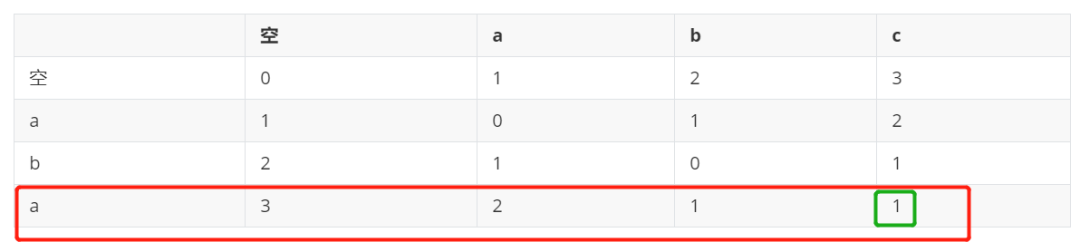
看到最终的编辑距离值是 1。1 满足小于等于maxEdit。所以其实该位置字符a[0] =‘a’ 是完全可以导致生成一个最终编辑距离<=maxEdit的相似匹配的。因此该文章的解释是完全错误的。那么到底该如何解释证明定理5呢？ 本文接下来创造性地给出定理4 的解释论证过程。这也是本文体现独创性的重要方面，因为相关的公开文献资料较少有能清晰且正确地阐述为什么Levenshtein DFA的求解输入符号集合Σ的Transitions()函数按照如下红框中所示这么写的：

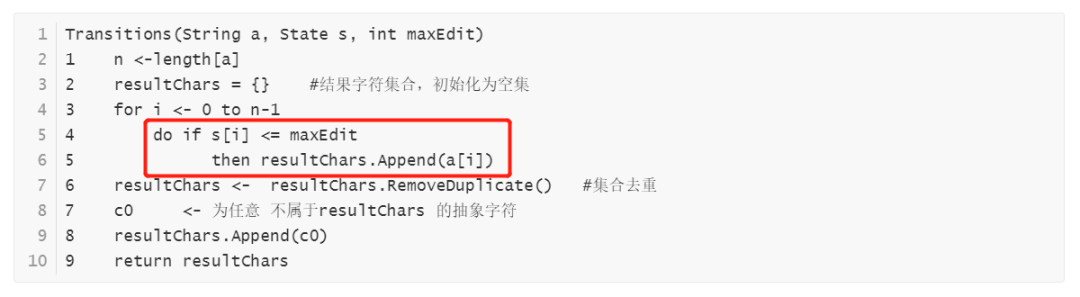
下面给出定理5证明过程

定理5证明：

令Set(a)是目标字符串a全部所包含字符去重后构成的集合， c0是满足 c0 ∉ Set(a)的任意字符，则根据定理3可知 字符c0必是求解输入符号集合Σ所必不可少需要包括的一个字符。再假设对于任意k 满足 0<= k <= n-1 且 s[k] > maxEdit ，我们此时将字符a[k] 与 特殊字符c0 进行对照考察。根据前文论述过的 Step步进函数伪代码如下所示：

Step(String a,  State s,  Char c)
 1   State snew = [0]
 2   for i <- 1 to length[a]
 3       do  cost = (a[i-1] == c ? 0 : 1)
 4           dist = Min(s[i-1] + cost, s[i] + 1, snew[i-1] +1 )
 5           snew.append( Min(dist, maxEdit+1) )
 6   return snew

考虑上述伪代码中第23行的迭代判断，对于c == a[k]的情况下，23循环过程只在i -1 == k时，cost 值会等于0，其他i迭代时，cost值都等于1。现在分2种情况考虑如下:

1. 当i -1 == k时

a) 对于c == a[k]的情况, 计算cost的值等于0,于是此时新的编辑距离dist = Min(s[i-1], s[i] +1, snew[i-1] + 1)，因为i -1== k，于是：

dist = Min(s[k], s[k+1] + 1,  snew[k] + 1)

又因为定理5题干前提条件令s[k] > maxEdit，根据定理1，所有大于maxEdit 的编辑距离值都可以用maxEdit + 1等价代替。于是有：

dist = Min(maxEdit + 1, s[k+1] + 1,  snew[k] + 1)

b) 对于 c == c0的情况,因为c0是任意不属于Set(a)集合的元素，所以c0 必不等于a[i-1],于是cost = 0,因为i -1 = k，于是有：

dist = Min(s[k], s[k+1] + 1,  snew[k] + 1)

同样结合定理1，得到：

dist = Min(maxEdit + 1, s[k+1] + 1, snew[k] + 1

可见在i-1 == k的情况，对应于 c == a[k] 或 c0， 新计算所得的状态dist值都为：Min(maxEdit + 1, s[k+1] + 1, snew[k] + 1)。因为根据定理1，所有大于maxEdit的值都可以等价替换为maxEdit， 因此 dist的值 只取决于 s[k+1] + 1 和 snew[k] + 1 二者的值。假设a[k]在字符串a中不重复（如果重复，那么其它位置的相同字符会根据它所处的位置重新判断是否满足定理5），则上述伪代码第3行迭代字符串a的任意位置t 满足t !=k，则a[t] 必不等于a[k], 同时考虑到c0是任意不属于Set(a)集合的元素, 同样有a[t]必不等于c0,即：迭代任意位置t != k 时，伪代码第4行 cost值 在c == a[k] 或c0时都等于0，也即：不论c = a[k]或c0， snew当前位置k+1的前一位置k的值snew[k]也必相等。同时 在c == a[k] 或c0时s[k+1]的值都是相同的，因此 二者在i-1==k位置计算所得的dist值是恒相等的。

2. 当i-1 != k时

还是在a[k]在字符串a。中不重复的假设下（如果重复，那么其它位置的相同字符会根据它所处的位置重新判断是否满足定理5），所有满足i -1 != k的位置i ,因 a[i] ！= a[k] 和 a[i] != c0同时成立，于是有：

dist = Min(s[k] + 1, s[k+1] + 1,  snew[k] + 1)

同样结合定理1，同时考虑到定理5题干前提条件s[k] > maxEdit，可得：

dist = Min(maxEdit + 1, s[k+1] + 1,  snew[k] + 1)

因此 dist的值 只取决于 s[k+1] + 1 和 snew[k] + 1 二者的值。雷同前面当 i -1 ==k 的情况，可知 这两值 s[k+1] + 1 和 snew[k] + 1在c == a[k] 和 c == c0两种情况也也分别都相等，因此可得：二者在i-1!=k位置计算所得的dist值也是恒相等的。

综合以上1和2两种情况，可得 对于任意k 满足 0<= k <= n-1 且 s[k] > maxEdit 的字符a[k]，其实与定理3，定理4中定义的任意一个不属于Set(a)即c0 ∉ Set(a)的字符时候完全等价的，即他们会生成完全一致的新的状态。因此， 根据定理4，特殊字符c0是必定会被纳入输入符号集合Σ代入状态转换函数用于生成新状态的，因此只需要纳入其中的c0字符考虑即可，在求解基于上一个状态s的输入符号集合Σ过程中必然可以不考虑k位置的字符a[k] 。定理5证明完毕。

由以上定理5的证明过程可知，并不是像上述引用的文章中给出的解释那样：一旦生成了>maxEdit的编辑距离的位置字符再次转换生成的新的最终的编辑距离就不会减小了。事实是完全可能再次减小的，之所以可以不考虑该位置的字符，是因为有等价的c0字符已经被考虑了。仅此而已。定理5虽然是很不起眼的一处代码，实则背后有着耐人寻味的理论依据。

最后说一下，为什么要如此大的篇幅来实施定理5所表达的处理逻辑，即：

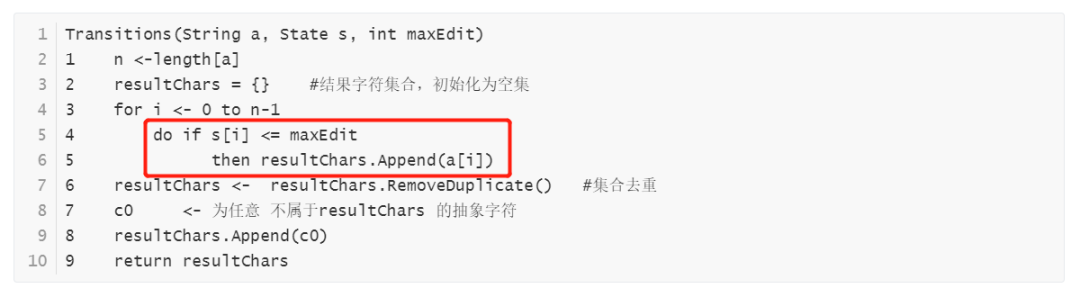
原因是为了减少不必要的计算Levenshtein DFA中所有状态的次数，提高构建Levenshtein DFA的效率。

至此，我们终于把 Leveshtein DFA的三大类要素：状态、转换函数和输入符号细节全部分析完毕。接下来我们给出Levenshtein DFA的伪代码实现，并给出效果图，最后分析时间复杂度。

注意：本文为了简化讨论，只讨论单字节字符的情况。对于多字节字符比如汉字字符有关的Levenshtein问题解决方案我们后续另行系列文章讨论。

4.3.2 构建 Levenshtein DFA和性能分析

本节将依次给出构建 Levenshtein DFA 的代码示例和性能分析定义状态：

对于目标字符串a, n = length[a], Levenshtein DFA的状态State 定义伪代码示意如下：

1   Class State {
2   public:
3      int hash();
4      int equal(const State& rhs);
5
6   private:
7      Arrays[0..n]    m_edits;  //编辑距离值的数组，长度为n+1，n = length[a]
8   }

可见 Levenshtein DFA的状态State 唯一数据成员就是长度为n+1 的LD编辑距离值的数组。因为State要被用于Hash表缓存，因此须定义hash()和equal()函数，两个函数实现逻辑也很简单，m_edits 数组全部元素分别相等在认为相等；每个元素值都需要被考虑组合生成hash值。

缓存的全局状态hash表结构式示意如下：

HashMap< State, HashMap<Char, State>  >  cachedStatesMap;

cachedStatesMap结构解决的问题是：基于上一个状态s,和某个输入字符c，能否有效转换或转换成什么样的新状态。

1. 定义Levenshtein DFA

   Levenshtein DFA 伪代码示意如下：

1   Class LevenshteinDFA {
2   public:
3   State           Start();  //初始状态
4   State           Step(State s, Char c); //状态转化
5   bool            IsMatch(State s);
6   bool            CanMatch(State s);
7   Array<Char>     Transitions(State s); //获取输入符号集合
8
9   private:
10  String        m_str;      //目标字符串
11  int           m_maxEdit;  // 最大编辑距离阈值，只能为1或2
12  }

初始状态伪代码示意如下：

State LevenshteinDFA::Start()
1   n <- length[ m_str ]
2   s = {0}
3   for i <- 1 to n
4       do s.Append(i)
5   return State(s)

状态转化函数Step()伪代码示意如下：

State  LevenshteinDFA::Step(State s, Char c )
 1   State snew = [s[0] + 1 ]
 2   for i <- 1 to length[m_str]
 3       do  cost = ( m_str[i-1] == c ? 0 : 1 )
 4           dist = Min(s[i-1] + cost,  s[i] + 1,  snew[i-1] +1 )
 5           snew.Append( Min(dist, m_maxEdit+1) )//根据定理1，maxEdit+1能代表所有无效的编辑距离值
 6   return snew

获取输入符号Transitions()伪代码示意如下：

Array<Char>  Transitions(State s)
1    n <- length[ m_str ]
2    resultChars = {}    #结果字符集合，初始化为空集
3    for i <- 0 to n-1
4        do if s[i] <= m_maxEdit
5              then resultChars.Append(m_str[i])
6    resultChars <-  resultChars.RemoveDuplicate() #集合去重
7    c0   <- 为任意 不属于resultChars 的抽象字符
8    resultChars.Append(c0)
9    return resultChars

IsMatch(s) 功能是判断s是否是最终可以被接受的状态，即最终与目标字符串是否相似。CanMatch(s) 功能是判断s是否是潜在可以被纳入考虑状态。根据LD的定义可知编辑距离值迭代结果只会不变或增大1，永远不会减小。显然如果s序列中的最小的编辑距离值都> maxEdit，那么该状态s后续怎么迭代也不可能产生<= maxEdit的新状态，于是这样的状态可以永远不被考虑，即not CanMatch。

IsMatch 和CanMatch 伪代码如下：

bool LevenshteinDFA::IsMatch(State s)
1    return s.Last() <= m_maxEdit //最后一个编辑距离值是否<= maxEdit

bool LevenshteinDFA::CanMatch(State s)
1    return s.Min() <= m_maxEdit //最小的编辑距离值是否<= maxEdit

1.初始化dfa和全局状态缓存变量cachedStatesMap

1  HashMap<State,HashMap<Char,State> >  cachedStatesMap;
2  LevenshteinDFA dfa(str, maxEdit);

递归搜索所有可能的状态转换关系并缓存至cachedStatesMap

RecursiveExploreDFA(State s)
1  if !cachedStatesMap.Contains(s)
2     then cachedStatesMap[s] <- HashMap();
3          for c in dfa.Transitions(s)
4              do  news <- Step(s,c)
5                  if  dfa.CanMatch(news)
6                      then RecursiveExploreDFA(news)
7                  cachedStatesMap[s][c] <- news

构建Levenshtein DFA

BuildLevenshteinDFA()
1  RecursiveExploreDFA(dfa.Start())

1. 判断字符串相似性

bool IsStringSimilar(String b)
1   n <- length[b]
2   s <- dfa.Start()
3   for i <- 1 to n
4       do if !cachedStatesMap.Contains(s) or !cachedStatesMap[s].Contains(b[i])
5          then return false
6          s <- cachedStatesMap[s][b[i]]
4   return dfa.IsMatch(s)

1. 性能分析

令目标字符串a 长度n = length[a] ; 待判断字符串b长度为m= length[b]；由上述伪代码容易分析得出：IsStringSimilar() 执行m次，复杂度为O(m); BuildLevenshteinDFA() 过程耗时取决于 RecursiveExploreDFA()函数递归次数和 RecursiveExploreDFA()第三行迭代Transitions()字符集和的次数。而Transitions()字符集和规模虽然之前做了优化，但规模最坏情况仍是O(n)。RecursiveExploreDFA()函数递归次数等于 dfa中最终状态个数sc。

下面分析一下sc的规模：首先容易知道长度为i的字符串 与 长度为j的字符串的LD编辑距离值至少为|i-j|。利用动态规划方法考虑一共可能出现多少种不同的状态值,如下图所示：

public static int LevenshteinDistance(String a, String b) {
    int[][] dist = new int[a.length()+1][b.length()+1];
    for (int i = 1; i <= a.length(); i++)
        dist[i][0] = i;
    for (int j = 1; j <= b.length(); j++)
        dist[0][j] = j;

    for (int j = 1; j <= b.length(); j++) {
        for (int i = 1; i <= a.length(); i++) {
            int cost = (a.charAt(i-1) == b.charAt(j-1) ? 0 : 1);
            int dist = Math.min(dist[i - 1][j] + 1, dist[i][j - 1] + 1);
            dist[i][j] = Math.min(dist, dist[i - 1][j - 1] + cost);
        }
    }
    return dist[a.length() - 1][b.length() - 1];
}

1. 上述伪代码第8行迭代待检查字符串b的每一个前缀子串b[…j]时，对应该前缀子串的该行编辑距离值中，只有 j-maxEdit ~ j+ maxEdit 一共2*maxEdit +1 列编辑距离的值有可能<=maxEdit。其它列的编辑距离值 必定都大于maxEdit,根据定理1，都可以用maxEdit +1 值等价代替。即当maxEdit=1时只有2*1 +1 = 3; 当maxEdit=2时只有2*2+1=5列编辑距离值<=maxEdit，其它列都是maxEdit+1。maxEdit=1时，<=maxEdit的值有0或1两种；maxEdit=2时<=maxEdit的取值有0,1,2三种；也就是说 所有编辑距离值组合中最多只有 2^3+1 或 3^5+1种组合，即最多只有9种或244种状态。因此对于固定的maxEdit （1或2）， 状态个数sc 也是常量值。

   综合以上可得，BuildLevenshteinDFA时间复杂度为O(sc * length[n]) 即O(n)，为线性的，而且更重要的是，BuildLevenshteinDFA过程是预处理过程，是一次性过程。而每次查找判断字符串b与a的相似性时，复杂度为O(length[b]),即O(m),也是线性的。这线性时间复杂度明显优于动态规划法的O(m * n)时间复杂度。

   最后给出一个目标字符串为a=“北京北站”,maxEdit=1构建的LevenshteinDFA示意图，图中阴影椭圆图形表示该状态是可接受的，即LD编辑距离<=1。字符*表示任意不属于目标字符串a所有包含字符集合{‘北’,‘京’,‘站’}的特殊字符。

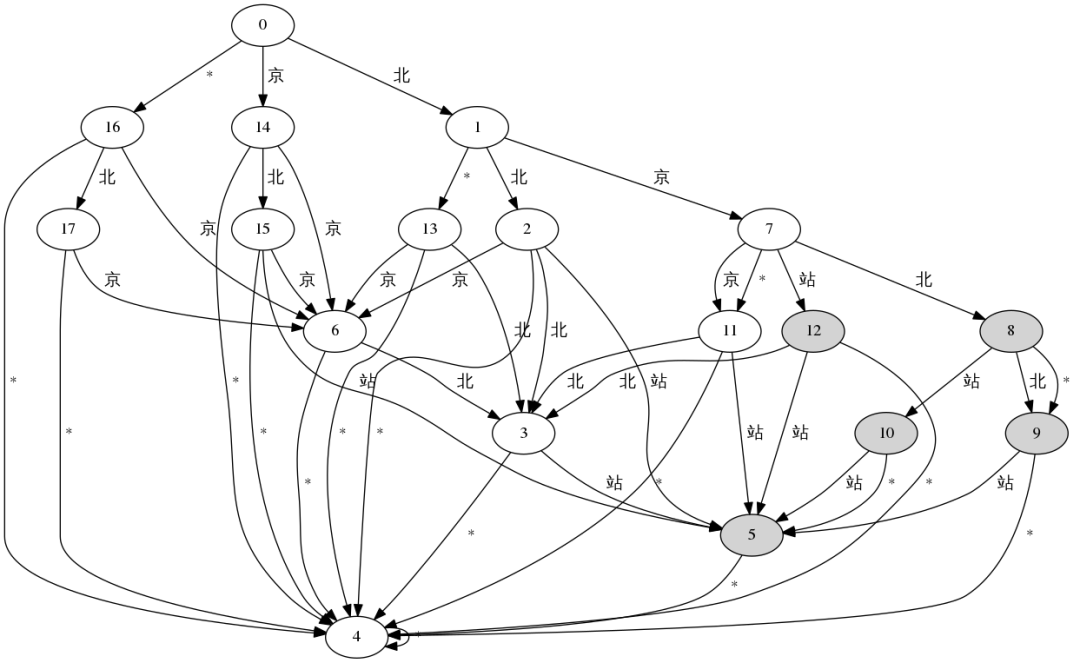
4.4 创新点：Damerau Levenshtein DFA

关于Damerau Levenshtein DFA，网络上很多实现过程都是错误的，缺乏正确理论论证支撑。本文创造性地提出了一种高效的Damerau Levenshtein DFA的构建技术，同时独创性地给出了严密的正确性论证过程。

本节仍然按照定义、分析和实现三部分展开讨论。

4.4.1 定义Damerau Levenshtein

通过前文第1节的介绍可知Damerau Levenshtein Distance(简称DLD）与Levenshtein Distance（简称LD）的唯一区别就是 状态转换的时候，下一个状态的生成除了依赖当前状态的DLD值外，还依赖于上一个DLD的值。具体来讲是：当最近两个相邻字符交叉相等时，下一个DLD的计算还需要考虑上一个DLD值+1。

下面示例代码展示了DLD的动态规划算法的实现过程，红色方框中逻辑即为DLD 比LD唯一多出的逻辑处理。不多不少，就多出这一处逻辑处理过程。

注意：为了便于表述，我们将下面红色方框中伪代码处理 特别地 成为 ”Damerau 条件分支”。 后文定理表述中会提到“Damerau 条件分支”表述。

容易分析得出，DLD的蛮力法和动态规划法时间复杂度都与LD完全一致。此处不再展开。

下面分析Damerau Levenshtein DFA确定有穷自动机的构建技术。

4.4.2 分析 Damerau Levenshtein DFA

分析Damerau Levenshtein DFA，我们仍然按照DFA 五大要素(M = ( S，Σ ，δ，s0，F ))和 3类要素（状态、转换函数、输入符号）的内容进行。

1. 状态

   Damerau Levenshtein DFA 之所以比Levenshtein DFA复杂，就是因为它的状态复杂。根据定义，生成的下一个状态的DLD序列值不仅与当前状态的DLD值有关，还可能在相邻字符交叉相等的情况下，与上一个状态的DLD有关。（LD不同的是只与上一个状态的LD值有关）。因此很自然地，将 上一个状态的DLD值序列 prevDists 和当前状态的DLD值序列 curDists，以及 prevDists 经由什么字符prevChar 转换生成了当前curDists。令字符串a为目标字符串，则Damerau Levenshtein DFA状态State伪代码如下：

Class  State {
   bool Equal(const State& s);
   int  Hash();

public:
   Array[0..n]       m_prevDists;//上一个状态的DLD值序列，n=length[a],不能为null
   Char              m_prevChar; //m_prevDists 经由m_prevChar转换生成了m_curDists，可以为null
   Array[0..n]       m_curDists; //当前状态的DLD值序列,可以为null

   String            m_str; //目标字符串
   int               m_maxEdit; //最大编辑距离阈值，必须为1或2
}

1. 通过前文4.3.2节对Levenshtein DFA的性能分析类比知道， m_prevDists或m_curDists的可能取值的数量最多可能为9种或244种。m_prevChar取值数量为length[a], 现在如果放任 m_prevDists、m_prevChar、m_curDists 三种变量组合，那么Damerau Levenshtein DFA 状态集合的规模将爆炸式增长，姑且称之为“状态爆炸”。根据对LD性能分析我们大体类比会猜测到 BuildDamerauLeveshteinDFA的时间复杂度大体也与DLD dfa的状态集合规模正相关。又因为构建DFA的过程就是缓存全部可能状态的过程。因此，这种单纯放任状态数量暴涨的朴素方式必然导致 构建DamerauLevenshtein DFA过程时间复杂度高，且耗费内存较大，不可取！

   如何解决“状态爆炸”问题，提高构建DamerauLevenshtein DFA的效率并减少其内存消耗呢？这是本文重要的创新点之一。 下面详细展开论述。

2. Damerau Levenshtein DFA状态消减策略

   消减状态数量本质上就是要把大量逻辑上可以等价对待状态视为1个状态即可。因为所有状态最终是要被缓存到全局Hash表中的。因此消减Damerau Levenshtein DFA状态 策略等价于 为State类数据结构定义一个逻辑完善且正确的 Equal()函数。

   下面给出Damerau Levenshtein DFA状态消减策略的一个定理。

   定理6：在构造目标字符串a的Damerau Levenshtein DFA时，

   对于任意状态s，如果不存在 任意一个k 满足 0 < k < length[a] ,使得

   1）a[k] != a[k-1]

   2）a[k] == s.m_prevChar

   3）s.m_prevDists[k-1] < Min( maxEdit, s.m_curDists[k] , s.m_curDists[k+1])

   以上3个条件同时成立，则 基于状态s为上一个状态的任意状态转换过程中对新编辑距离的计算逻辑可忽略“Damerau 条件分支”，这样不影响最终构建Damerau Levenshtein DFA结果的正确性。

   注：“Damerau 条件分支”前文4.4.1节提到过。

证明：

反证法，假定任意存在一个k 满足 0 < k < length[a]，使得 定理6中3个条件同时成立，那么就可能存在1个字符c == a[k-1] 基于状态s进行状态转换，因为c == a[k-1] 且a[k] == s.m_prevChar , 同时a[k] != a[k-1]， 即相邻两个字符不相等，但交叉相等，于是根据DLD的定义，新编辑距离值计算必定从形式包含了“Damerau 条件分支”；于是，新的编辑距离值dist 必定为 s.m_curDists[k]+1, s.m_curDists[k+1] + 1, s.m_prevDists[k-1] + 1 三者中的最小值，又根据定理6条件3)得知，s.m_prevDists[k-1] 是 s.m_curDists[k] 和 s.m_curDists[k+1] 二者的最小值，因此dist值必定恒等于 s.m_prevDists[k-1] + 1 。根据条件3)同时s.m_prevDists[k-1] < maxEdit， 因此dist < maxEdit +1 <= maxEdit。即 最终的新的编辑距离值dist是有效的，且其值来源于 ““Damerau 条件分支””。因此新的编辑距离迭代实质上也是发生在了“Damerau 条件分支” 。即：只要任意存在一个k 满足 0 < k < length[a]，使得 定理6中3个条件同时成立，那么基于状态s为上一个状态，字符c==a[k-1]的状态转换过程中对新编辑距离的计算逻辑 就必定 从形式和实质上都包含“Damerau 条件分支”。反之，迭代目标字符串的每一个位置k，如果都不能使得下一次状态转换逻辑计算过程包含“Damerau 条件分支”，则 该基于该状态s为上一个状态的转换实际就是一个不包含“Damerau 条件分支”的转换，忽略“Damerau 条件分支”，不影响最终构建Damerau Levenshtein DFA结果的正确性。证明完毕。

根据定理6可以给出如下伪代码,判断状态s是否可能是实质包含“Damerau 条件分支”，即 IsPossibleDamerau()

IsPossibleDamerau(State s)
1   n <- length[a]
2   for i <- 1 to n-1
3       do if (a[i] != a[i-1] and a[i] == s.m_prevChar
4                   and s.m_prevDists[i-1] < Min(maxEdit, s.curDists[i], s.curDists[i+1]) )
5            then return True
6   return False

于是根据IsPossibleDamerau，本文给出State的Equal() 伪代码，按照如下示意：

bool  State::Equal(const State& rhs)
1    if  m_curDists != rhs.m_curDists
2        then return False
3    isIn    <- m_str.Contains(s.m_prevChar)
4    isInRhs <- m_str.Contains(rhs.m_prevChar)
5    if isIn != isInRhs
6       then return False
7    else if False == isIn
8            then return True
9         else if m_preChar != rhs.m_prevChar
10                then return False
11                else if IsPossibleDamerau(*this) or IsPossibleDamerau(rhs)
12                        then return m_prevDists == rhs.m_prevDists
13                        else return True

1. 此外因为State要被缓存到全局，所以不可以避免要对状态进行散列hash， Hash()函数逻辑很简单，直接按照m_curDists值去散列即可。

2. 转换函数

   转换函数比较简单，直接按照DLD的定义编写即可。

3. 输入符号

   DamerauLevenshtein DFA的输入符号方面，Transitions() 函数实现过程同样遵循定理5。理解过程与Levenshtein 相同。

4.4.3 构建Damerau Levenshtein DFA和性能分析

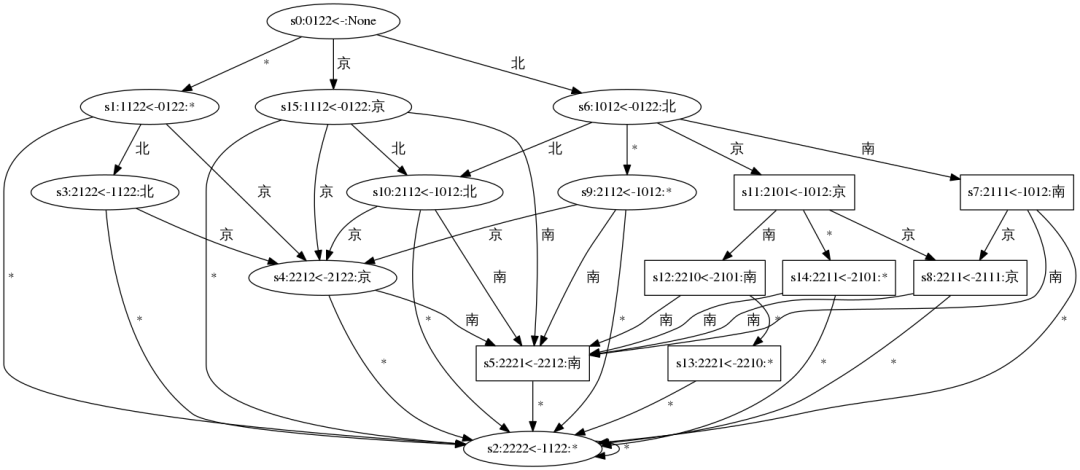
上图给出了目标字符串a=“北京南”,最大编辑距离阈值maxEdit=1的DamerauLevenshtein DFA的示意图。图中方形框 表示状态可以被接受，即满足字符串相似性。图中方框中文本表示状态来源关系，如：s3:2122from1122:北 含义是：当前状态s3,DLD序列值是{2,1,2,2}, 它的上一个状态的DLD序列值是：{1,1,2,2}，经过字符是北。容易分析出图中大量状态被等价归一化了，减小了内存消耗和处理时间消耗。

DamerauLevenshtein DFA的类定义，构建方法以及查找字符串是否满足DamerauLevenshtein相似性的伪代码基本同前文Levenshtein DFA差别不大。主要的差异是状态State相关的逻辑，前文已经论述过。

最后，分析一下DamerauLevenshtein DFA方法的时间复杂度。预处理构建DamerauLevenshtein DFA 过程为O(sc*length[a]),sc为状态集合数量，length[a]为目标字符串长度。在sc被大量等价归一化后，仍为O(length[a])。每一次查找字符串是否满足相似性条件的过程时间复杂度仍旧为O(length[b]),b为待检查字符串。综合来看，DamerauLevenshtein DFA 解决字符串相似问题的时间复杂度也是线性的。

总结与讨论

至此，基于Levenshtein和Damerau Levenshtein自动机技术，高效求解搜索引擎中相似字符串快速查找问题的技术原理全部论述完毕。总览全文，本文创造性地提出了一种Damerau Levenshtein自动机的有效构建算法，并创造性地给出了利用Levenshtein自动机和Damerau Levenshtein自动机技术，解决快速查找相似字符串问题实现方案的正确性理论依据论证。

与本文主题相关的未解决的留待后续继续讨论的主题可能还有：

1. 本文提出的状态消�