大规模特征向量检索算法总结
编辑整理 梁尔舒
向量检索基本概念
向量从表现形式上就是一个一维数组。我们需要解决的问题是使用下面的公式度量距离寻找最相似的 K 个向量。

- 欧式距离: 两点间的真实距离,值越小,说明距离越近;
- 余弦距离:就是两个向量围成夹角的 cosine 值,cosine 值越大,越相似;
- 汉明距离:一般作用于二值化向量,二值化的意思是向量的每一列只有 0 或者 1 两种取值。
- 汉明距离的值就两个向量每列数值的异或和,值越小说明越相似,一般用于图片识别;
- 杰卡德相似系数:\* 把向量作为一个集合,所以它可以不仅仅是数字代表,也可以是其他编码,比如词,该值越大说明越相似,一般用于相似语句识别;
因为向量检索场景的向量都是维度很高的,比如 256,512 位等,计算量很大,在工业上,常用的大规模特征向量索引方法主要以倒排、 PQ 及其变种、基于树的方法(比如 KD 树)和 哈希(典型代表 LSH 和 ITQ)为主流。
首先从检索的召回率上来评估,基于图的索引方法要优于目前其他一些主流 ANN 搜索方法,比如乘积量化方法(PQ、OPQ)、哈希方法等。虽然乘积量化方法的召回率不如 HNSW(基于图的代表方法),但由于乘积量化方法具备内存耗用更小、数据动态增删更灵活等特性,使得在工业检索系统中,在对召回率要求不是特别高的场景下,乘积量化方法仍然是使用得较多的一种索引方法,淘宝(详见 Fast Approximate Nearest Neighbor Search With The Navigating Spreading-out Graph)、蘑菇街等公司均有使用。乘积量化和 HNSW 特性对比如下:
特性OPQHNSW内存占用小大召回率较高高数据动态增删灵活不易
基于图 ANN 方法由于数据在插入索引的时候,需要计算(部分)数据间的近邻关系,因而需要实时获取到到数据的原始特征,几乎所有基于图 ANN 的方法在处理该问题的时候,都是直接将原始特征加载在内存(索引)里,从而造成对内存使用过大,至于召回率图 ANN 方法要比基于量化的方法要高,这个理解起来比较直观。
向量检索算法
KNN 算法
KNN 算法表示的是准确的召回 topK 的向量,这里主要有两种算法,一种是 KDTtree,一种是 Brute Force。我们首先分析了 KDTree 的算法,发现 KDTree 并不适合高维向量召回,于是我们实现的 ES 的 Brute Force 插件,并使用了一些 Java 技巧进行加速运算。
KDTree 算法
简单来讲,就是把数据按照平面分割,并构造二叉树代表这种分割,在检索的时候,可以通过剪枝减少搜索次数。
构建树
KD 树选择从哪一维度进行开始划分的标准,采用的是求每一个维度的方差,然后选择方差最大的那个维度开始划分。为何要选择方差作为维度划分选取的标准?我们知道,方差的大小可以反映数据的波动性。方差大表示数据波动性越大,选择方差最大作为划分空间标准的好处在于,可以使得所需的划分面数目最小,反映到树的数据结构上,可以使得我们构建的 KD 树的树深度尽可能小。
以二维平面点 (x,y) 的集合 (2,3),(5,4),(9,6),(4,7),(8,1),(7,2) 为例构建树:
-
构建根节点时,x 维度上面的方差较大,如上点集合在 x 维从小到大排序为
(2,3),(4,7),(5,4),(7,2),(8,1),(9,6),其中值为(7,2)。 -
(2,3),(4,7),(5,4)挂在(7,2)节点的左子树,(8,1),(9,6)挂在(7,2)节点的右子树。 -
构建
(7,2)节点的左子树时,点集合(2,3),(4,7),(5,4)此时的切分维度为y,中值为(5,4)作为分割平面,(2,3)挂在其左子树,(4,7)挂在其右子树。 -
构建
(7,2)节点的右子树时,点集合(8,1),(9,6)此时的切分维度也为y,中值为(9,6)作为分割平面,(8,1)挂在其左子树。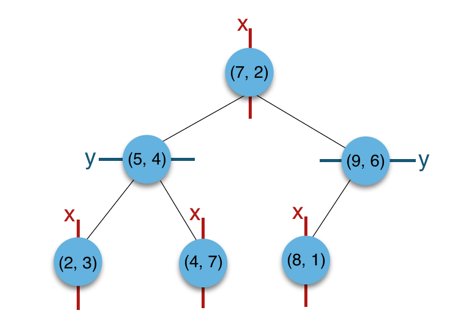
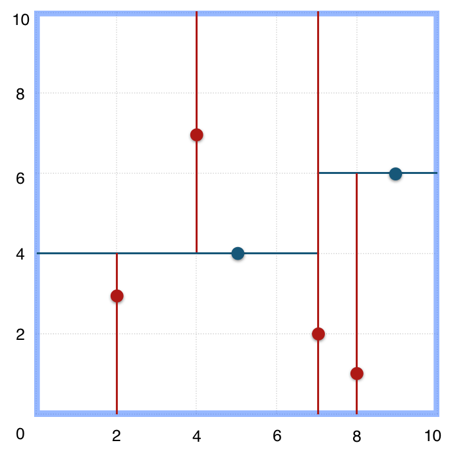
上述的构建过程结合下图可以看出,构建一个 KDTree 即是将一个二维平面逐步划分的过程。
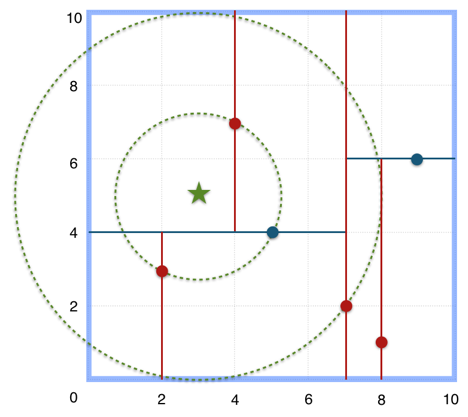
搜索 (3,5) 的最近邻:
- 首先从根节点
(7,2)出发,将当前最近邻设为(7,2),对该 KDTree 作深度优先遍历。以(3,5)为圆心,其到(7,2)的距离为半径画圆(多维空间为超球面),可以看出(8,1)右侧的区域与该圆不相交,所以(8,1)的右子树全部忽略。 - 接着走到
(7,2)左子树根节点(5,4),与原最近邻对比距离后,更新当前最近邻为(5,4)。以(3,5)为圆心,其到(5,4)的距离为半径画圆,发现(7,2)右侧的区域与该圆不相交,忽略改厕所有节点,这样(7,2)的整个右子树被标记为已忽略。 - 遍历完
(5,4)的左右叶子节点,发现与当前最优距离相等,不更新最近邻。所以(3,5)的最近邻为(5,4)。
KDTree 的查询复杂度为O(kn^{(k-1)/k}), k 表示维度, n 表示数据量。说明 k 越大,复杂度越接近线性,所以它并不适合高维向量召回。
Brute Force
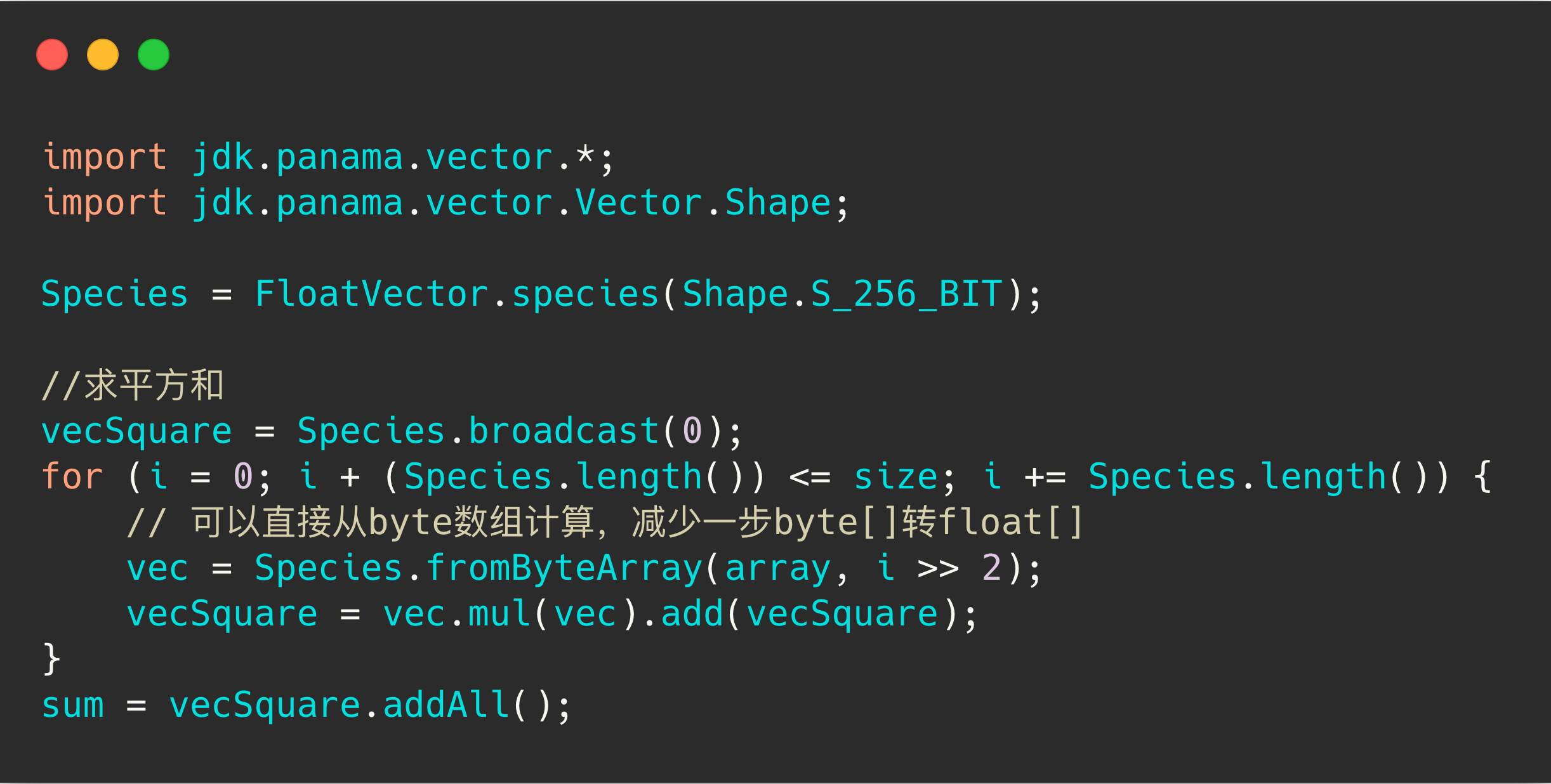
顾名思义,就是暴力比对每一条向量的距离,我们使用 BinaryDocValues 实现了 ES 上的 BF 插件。更进一步,我们要加速计算,所以使用了 Java Vector API 。Java Vector API 是在 OpenJDK project Panama 项目中的,它使用了 SIMD 指令优化
LSH 算法
Local Sensitive Hashing,局部敏感哈希,我们可以把向量通过平面分割做 hash。如下图所示, 0 表示点在平面的左侧, 1 表示点在平面的右侧,然后对向量进行多册 hash,可以看到 hash 值相同的点都比较靠近,所以在 hash 之后,我们只需要计算 hash 值类似的向量,就能较准确地召回 topK。
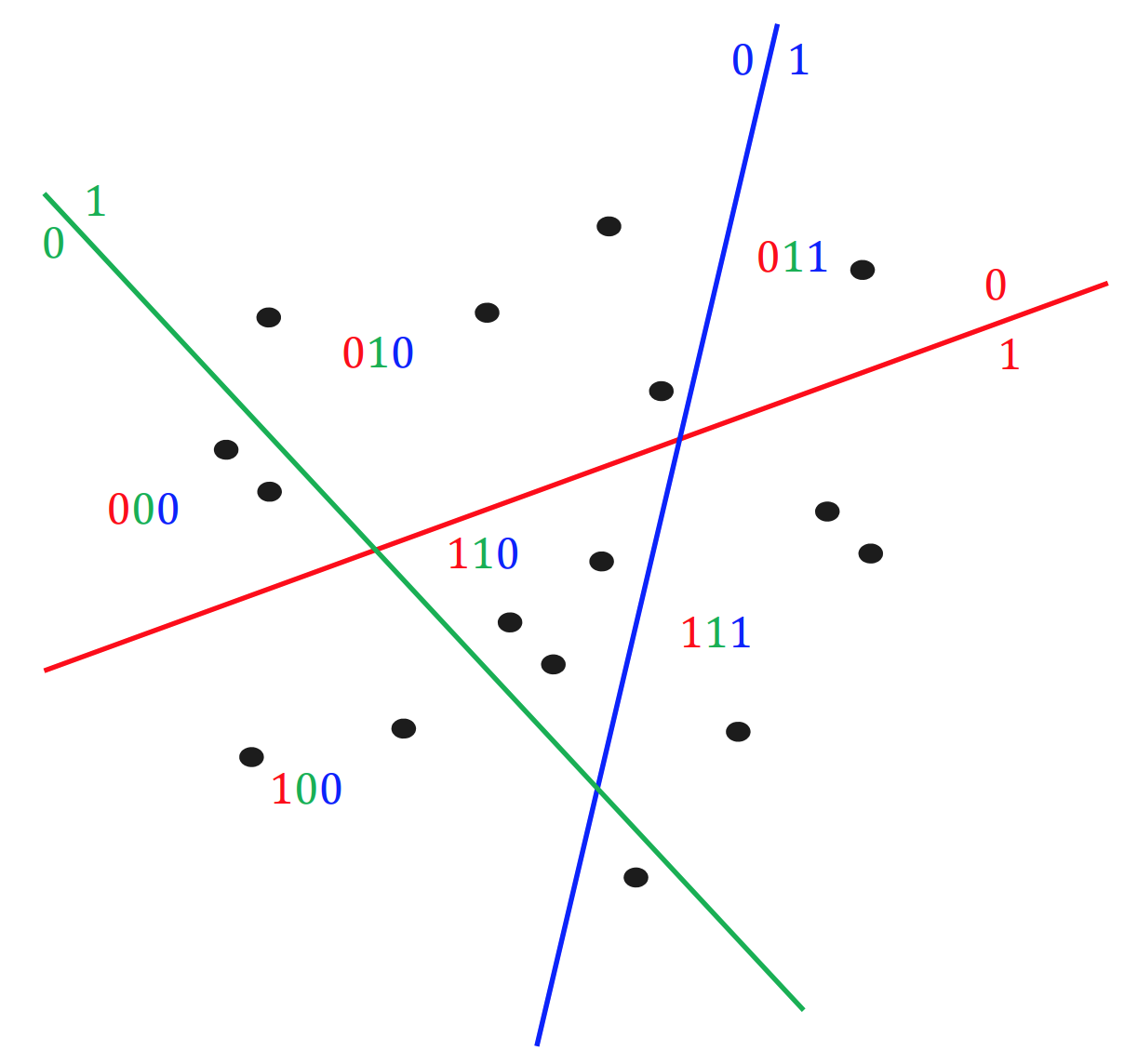
下面是一些需要重点理解的知识:
1. 局部敏感是啥意思?
当一个函数(或者更准确的说,哈希函数家族)具有如下属性的时候,我们说该哈希函数是局部敏感的:相似的样本点对比相远的样本点对更容易发生碰撞。
2. 用哈希为什么可以加速查找?
对于 Brute Force 搜索,需要遍历数据集中的所有点,而使用哈希,我们首先找到查询样本落入在哪个 cell(即所谓的桶)中,如果空间的划分是在我们想要的相似性度量下进行分割的,则查询样本的最近邻将极有可能落在查询样本的 cell 中,如此我们只需要在当前的 cell 中遍历比较,而不用在所有的数据集中进行遍历。
3. 为什么要用多表哈希?
对于单表哈希,当哈希函数数目 K 取得太大,查询样本与其对应的最近邻落入同一个桶中的可能性会变得很微弱,针对这个问题,我们可以重复这个过程 L 次,从而增加最近邻的召回率。这个重复 L 次的过程,可以转化为构建 L 个哈希表,这样在给定查询样本时,我们可以找到 L 个哈希桶(每个表找到一个哈希桶),然后我们在这 L 个哈希表中进行遍历。这个过程相当于构建了 K*L 个哈希函数(注意是相当,不要做等价理解)。
4. 多表哈希中哈希函数数目 K 和哈希表数目 L 如何选取?
哈希函数数目 K 如果设置得过小,会导致每一个哈希桶中容纳了太多的数据点,从而增加了查询响应的时间;而当 K 设置得过大时,会使得落入每个哈希桶中的数据点变小,而为了增加召回率,我们需要增加 L 以便构建更多的哈希表,但是哈希表数目的增加会导致更多的内存消耗,并且也使得我们需要计算更多的哈希函数,同样会增加查询相应时间。通过选取合理的 K 和 L,我们可以获得比线性扫描极大的性能提升。
5. Multiprobe LSH 是为了解决什么问题?
多 probe LSH 主要是为了提高查找准确率而引入的一种策略。首先解释一下什么是 Multiprobe。对于构建的L个哈希表,我们在每一个哈希表中找到查询样本落入的哈希桶,然后再在这个哈希桶中做遍历,而 Multiprobe 指的是我们不止在查询样本所在的哈希桶中遍历,还会找到其他的一些哈希桶,然后这些找到的T个哈希桶中进行遍历。这些其他哈希桶的选取准则是:跟查询样本所在的哈希桶邻近的哈希桶,“邻近”指的是汉明距离度量下的邻近。
通常,如果不使用 Multiprobe,我们需要的哈希表数目L在 100 到 1000 之间,在处理大数据集的时候,其空间的消耗会非常的高,幸运地是,因为有了上面的 Multiprobe 的策略,LSH 在任意一个哈希表中查找到最近邻的概率变得更高,从而使得我们能到减少哈希表的构建数目。
综上,对于 LSH,涉及到的主要的参数有三个:
- L:哈希表(每一个哈希表有K个哈希函数)的数目
- K:每一个哈希表的哈希函数(空间划分)数目
- T: 近邻哈希桶的数目,即 the number of probes
这三个设置参数可以按照如下顺序进行:首先,根据可使用的内存大小选取L,然后在K和T之间做出折中:哈希函数数目K越大,相应地,近邻哈希桶的数目的数目
T也应该设置得比较大,反之K越小,L也可以相应的减小。获取K和L最优值的方式可以按照如下方式进行:对于每个固定的K,如果在查询样本集上获得了我们想要的精度,则此时 T的值即为合理的值。在对 T进行调参的时候,我们不需要重新构建哈希表,甚至我们还可以采用二分搜索的方式来加快 T$ 参数的选取过程。
乘积量化
乘积量化( Product Quantization, PQ)是一种非常经典实用的矢量量化索引方法,在工业界向量索引中已得到广泛的应用,并作为主要的向量索引方法,在 Faiss 中有非常高效的实现。乘积量化的核心思想是分段(划分子空间)和聚类,或者说具体应用到 ANN 近似最近邻搜索上, KMeans 是 PQ 乘积量化子空间数目为 1 的特例。
矢量量化方法,即 Vector Quantization,其具体定义为: 将一个向量空间中的点用其中一个有限子集来进行编码的过程。
PQ 乘积量化生成码本和量化的过程可以用如下图示来说明:
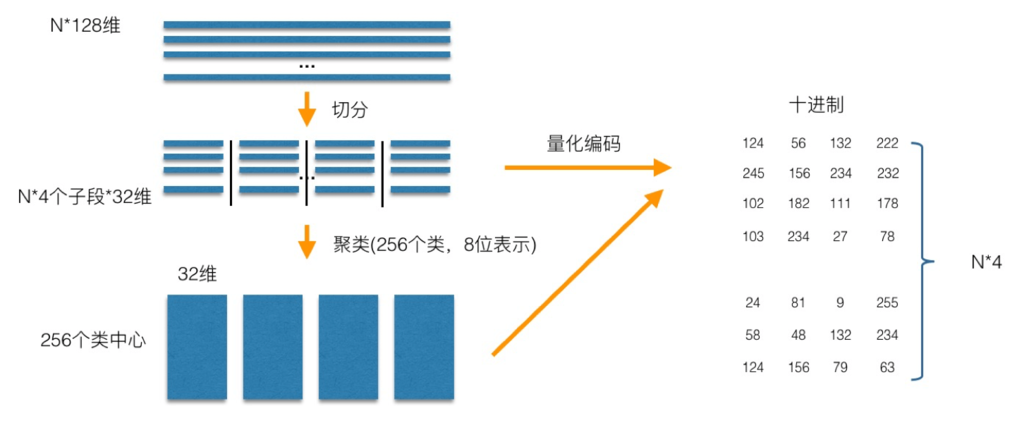
在训练阶段,针对 N 个训练样本,假设样本维度为 128 维,我们将其切分为 4 个子空间,则每一个子空间的维度为 32 维,然后我们在每一个子空间中,对子向量采用 KMeans 对其进行聚类(图中示意聚成 256 类),这样每一个子空间都能得到一个码本。这样训练样本的每个子段,都可以用子空间的聚类中心来近似,对应的编码即为类中心的 ID。如图所示,通过这样一种编码方式,训练样本仅使用很短的一个编码得以表示,从而达到量化的目的。对于待编码的样本,将它进行相同的切分,然后在各个子空间里逐一找到距离它们最近的类中心,然后用类中心的 id 来表示它们,即完成了待编码样本的编码。
正如前面所说的,在矢量量化编码中,关键是码本的建立和码字的搜索算法,在上面,我们得到了建立的码本以及量化编码的方式。剩下的重点就是查询样本与 dataset 中的样本距离如何计算的问题了。
在查询阶段, PQ 同样在计算查询样本与 dataset 中各个样本的距离,只不过这种距离的计算转化为间接近似的方法而获得。 PQ 乘积量化方法在计算距离的时候,有两种距离计算方式,一种是对称距离,另外一种是非对称距离。非对称距离的损失小(也就是更接近真实距离),实际中也经常采用这种距离计算方式。下面过程示意的是查询样本来到时,以非对称距离的方式(红框标识出来的部分)计算到 dataset 样本间的计算示意:
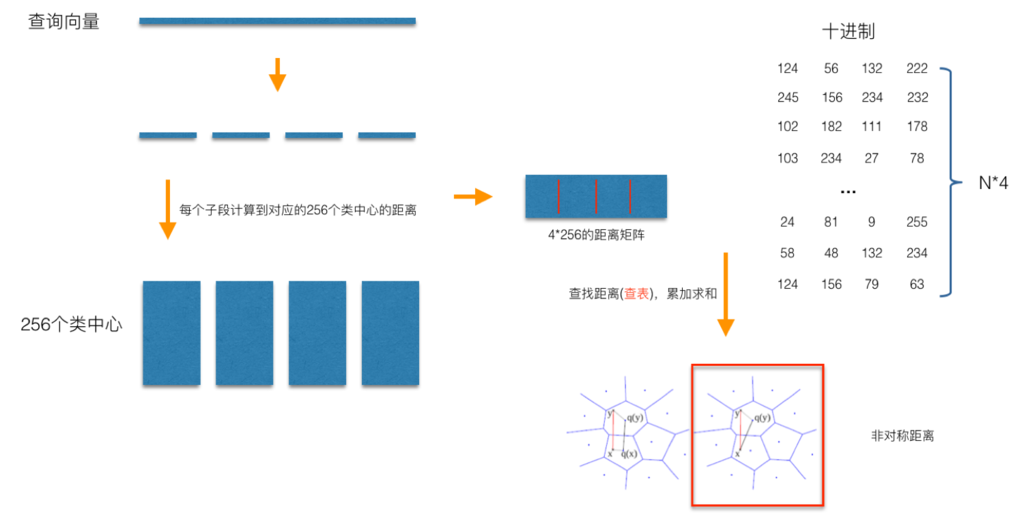
具体地,查询向量来到时,按训练样本生成码本的过程,将其同样分成相同的子段,然后在每个子空间中,计算子段到该子空间中所有聚类中心的距离,如图中所示,可以得到 4*256 个距离,这里为便于后面的理解说明,可以把这些算好的距离称作距离表。在计算库中某个样本到查询向量的距离时,比如编码为 (124,56,132,222) 这个样本到查询向量的距离时,我们分别到距离表中取各个子段对应的距离即可,比如编码为 124 这个子段,在第 1 个算出的 256 个距离里面把编号为 124 的那个距离取出来就可,所有子段对应的距离取出来后,将这些子段的距离求和相加,即得到该样本到查询样本间的非对称距离。所有距离算好后,排序后即得到我们最终想要的结果。
从上面这个过程可以很清楚地看出 PQ 乘积量化能够加速索引的原理:即将全样本的距离计算,转化为到子空间类中心的距离计算。比如上面所举的例子,原本 brute-force search 的方式计算距离的次数随样本数目 N 成线性增长,但是经过 PQ 编码后,对于耗时的距离计算,只要计算 4*256 次,几乎可以忽略此时间的消耗。另外,从上图也可以看出,对特征进行编码后,可以用一个相对比较短的编码来表示样本,自然对于内存的消耗要大大小于 brute-force search 的方式。
在某些特殊的场合,我们总是希望获得精确的距离,而不是近似的距离,并且我们总是喜欢获取向量间的余弦相似度(余弦相似度距离范围在 [-1,1] 之间,便于设置固定的阈值),针对这种场景,可以针对 PQ 乘积量化得到的前 top@K 做一个 brute-force search 的排序。
倒排乘积量化 倒排乘积量化
倒排乘积量化( IVFPQ)是 PQ 乘积量化的更进一步加速版。其加速的本质逃不开在最前面强调的加速原理: brute-force 搜索的方式是在全空间进行搜索,为了加快查找的速度,几乎所有的 ANN 方法都是通过对全空间分割,将其分割成很多小的子空间,在搜索的时候,通过某种方式,快速锁定在某一(几)个子空间,然后在该(几个)子空间里做遍历。在上一小节可以看出, PQ 乘积量化计算距离的时候,距离虽然已经预先算好了,但是对于每个样本到查询样本的距离,还是得老老实实挨个去求和相加计算距离。但是,实际上我们感兴趣的是那些跟查询样本相近的样本(姑且称这样的区域为感兴趣区域),也就是说老老实实挨个相加其实做了很多的无用功,如果能够通过某种手段快速将全局遍历锁定为感兴趣区域,则可以舍去不必要的全局计算以及排序。倒排 PQ 乘积量化的”倒排“,正是这样一种思想的体现,在具体实施手段上,采用的是通过聚类的方式实现感兴趣区域的快速定位,在倒排 PQ 乘积量化中,聚类可以说应用得淋漓尽致。
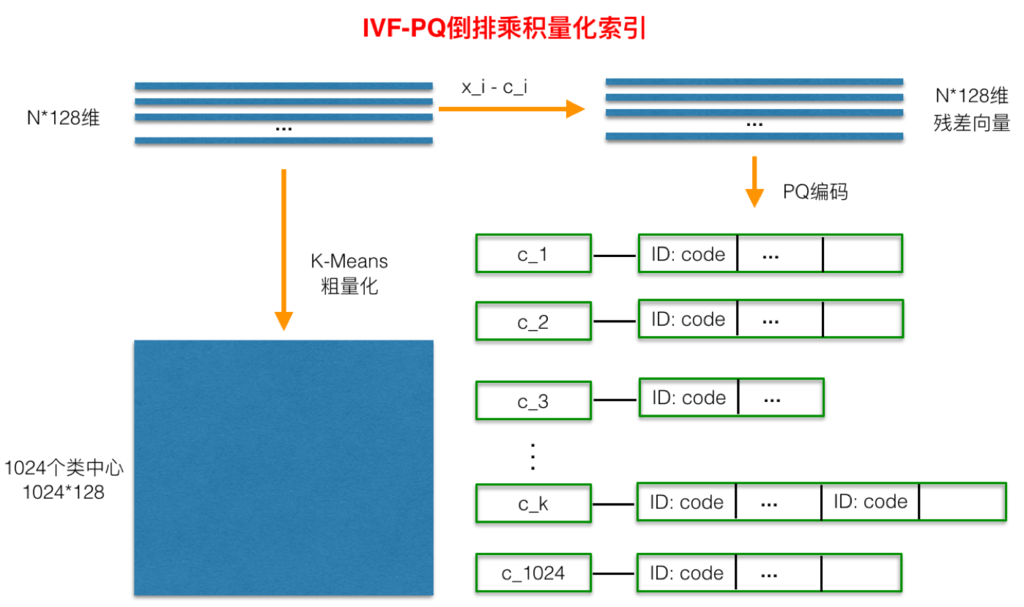
在 PQ 乘积量化之前,增加了一个粗量化过程。具体地,先对 N 个训练样本采用 KMeans 进行聚类,这里聚类的数目一般设置得不应过大,一般设置 1024 差不多,这种可以以比较快的速度完成聚类过程。得到聚类中心后,针对每一个样本 x_i,找到其距离最近的类中心 c_i 后,两者相减得到样本 x_i 的残差向量( x_i - c_i),后面剩下的过程,就是针对( x_i - c_i)的 PQ 乘积量化过程,此过程不再赘述。
在查询的时候,通过相同的粗量化,可以快速定位到查询向量属于哪个 c_i(即在哪一个感兴趣区域),然后在该感兴趣区域按上面所述的 PQ 乘积量化距离计算方式计算距离。
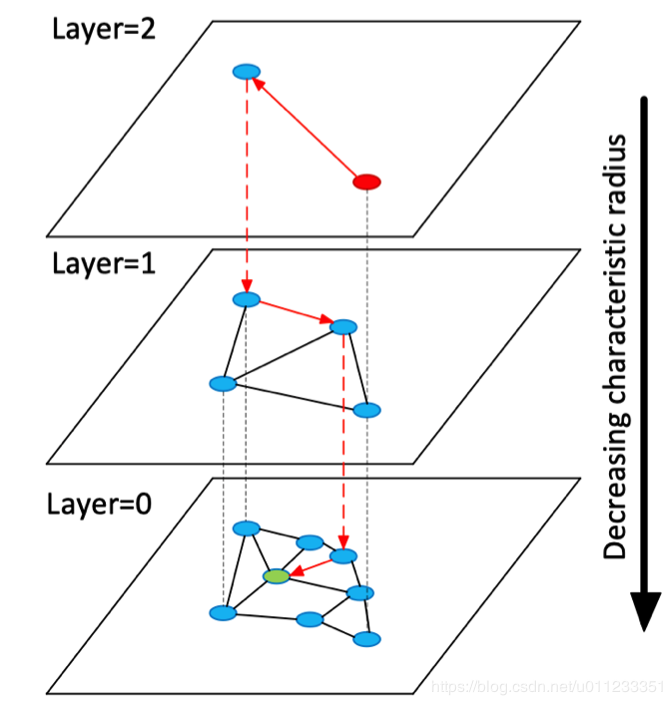
HNSW 算法(基于图的方法)
讲 HNSW 算法之前,我们先来讲 NSW 算法,如下图,它是一个顺序构建图流程:
- 例如第 5 次构造 D 点的流程;
- 构建的时候,我们约定每次加入节点只连 3 条边,防止图变大,在实际使用中,要通过自身的数据;
- 随机一个节点,比如 A,保存下与 A 的距离,然后沿着 A 的边遍历,E 点最近,连边。然后再重新寻找,不能与之前重复,直到添加完 3 条边;
查找流程包含在了插入流程中,一样的方式,只是不需要构建边,直接返回结果。

HNSW 算法是 NSW 算法的分层优化,借鉴了 skiplist 算法的思想,提升查询性能,开始先从稀疏的图上查找,逐渐深入到底层的图。
总结
以基于 PQ 的量化方法在工业界最为实用,基于图的 ANN 方法,在规模不是特别大但对召回要求非常高的检索场景下,是非常适用的。除此之外,图 ANN 方法可以和 OPQ 结合起来适用,来提高 OPQ 的召回能力,具体可以阅读 Revisiting the Inverted Indices for Billion-Scale Approximate Nearest Neighbors 和 Link and code: Fast indexing with graphs and compact regression codes 这两篇文章。
基于图的方法的突出优点是召回率高,在一开始有三个缺点,分别为速度慢、数据动态增删困难、内存占用大。这几年,速度通过很多方法已经有很大提高。而数据动态增删困难主要是因为,插入删除数据后,需要重新构建近邻图。
所以,目前基于图的方法主要在于内存占用大的缺点,其实问题主要在于为了高召回率,将原数据读到内存中,PQ 利用的是聚类中心来粗表示数据点。
参考
https://www.sofastack.tech/blog/antfin-zsearch-vector-search/
[http://blog.rexking6.top/2019/01/27/ANN-Search%E5%8F%8A%E4%B8%
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/%E4%BA%92%E8%81%94%E7%BD%91/%E5%A4%A7%E8%A7%84%E6%A8%A1%E7%89%B9%E5%BE%81%E5%90%91%E9%87%8F%E6%A3%80%E7%B4%A2%E7%AE%97%E6%B3%95%E6%80%BB%E7%BB%93/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


