回归是用于建模和分析变量之间关系的一种技术，常用来处理预测问题。博文介绍了常见的 五种回归算法和各自的特点，其中不仅包括常见的线性回归和多项式回归，而且还介绍了能用于高维度和多重共线性的情况的 Ridge回归、Lasso回归、ElasticNet回归，了解它们各自的优缺点能帮助我们在实际应用中选择合适的方法。

编译 | 专知

参与 | Yingying

添加微信：MLAPython

（姓名-单位-方向）

即可加入机器学习交流群

线性和逻辑斯蒂（Logistic）回归通常是是机器学习学习者的入门算法，因为它们易于使用和可解释性。然而，尽管他们简单但也有一些缺点，在很多情况下它们并不是最佳选择。实际上存在很多种回归模型，每种都有自己的优缺点。

在这篇文章中，我们将介绍5种最常见的回归算法及特点。我们很快就会发现，很多算法只在特定的情况和数据下表现良好。

线性回归（Linear Regression）

回归是用于建模和分析变量之间关系的一种技术，分析变量是如何影响结果的。线性回归是指完全由线性变量组成的回归模型。从简单情况开始，单变量线性回归（Single Variable Linear Regression）是一种用于使用线性模型来建模单个输入自变量（特征变量）和输出因变量之间关系的技术。

更一般的情况是多变量线性回归（Multi Variable Linear Regression），它体现了为多个独立输入变量（特征变量）与输出因变量之间的关系。该模型保持线性，因为输出是输入变量的线性组合。我们可以对多变量线性回归建模如下：

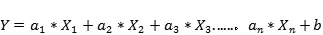
其中是系数，是变量，是偏置。正如我们所看到的，这个函数只有线性关系，所以它只适用于建模线性可分数据。这很容易理解，因为我们只是使用系数权重来加权每个特征变量的重要性。我们使用随机梯度下降（SGD）来确定这些权重 和偏置b。具体过程如下图所示：

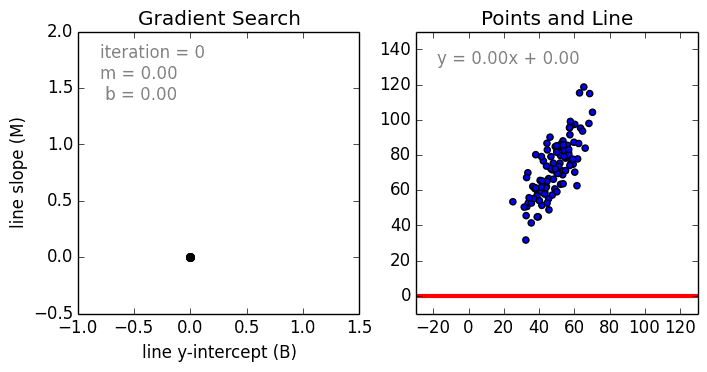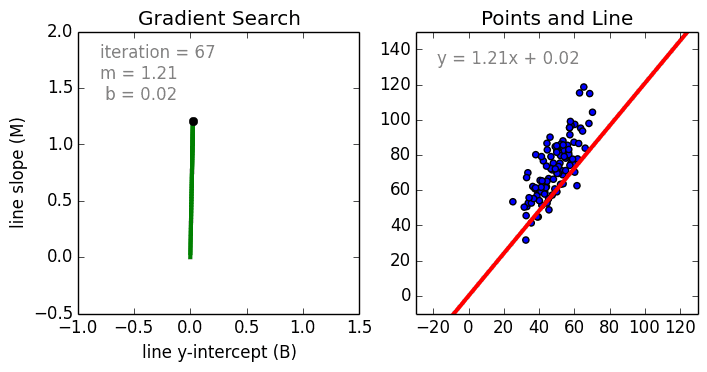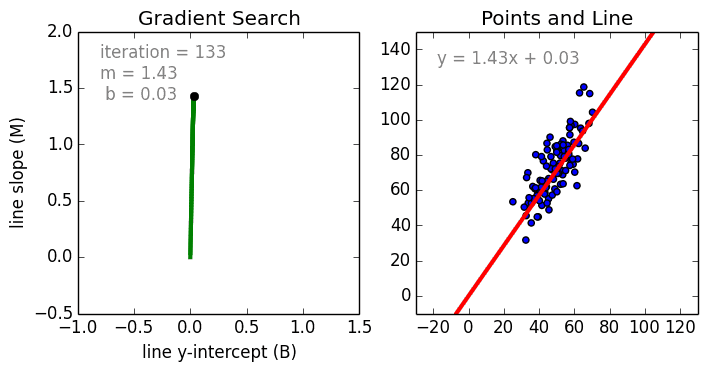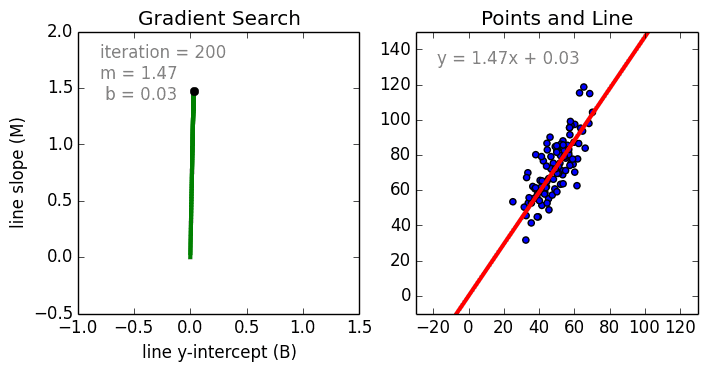
线性回归的几个关键点：

• 建模快速简单，特别适用于要建模的关系不是非常复杂且数据量不大的情况。

• 有直观的理解和解释。

• 线性回归对异常值非常敏感。

多项式回归（Polynomial Regression）

当我们要创建适合处理非线性可分数据的模型时，我们需要使用多项式回归。在这种回归技术中，最佳拟合线不是一条直线，而是一条符合数据点的曲线。对于一个多项式回归，一些自变量的指数是大于1的。例如，我们可以有这下式：

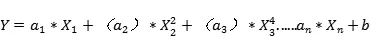
一些变量有指数，其他变量没有。然而，选择每个变量的确切指数自然需要当前数据集合与最终输出的一些先验知识。请参阅下面的图，了解线性与多项式回归的比较。

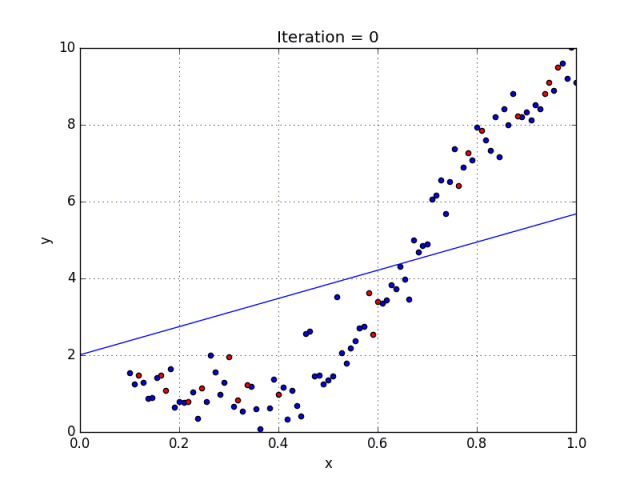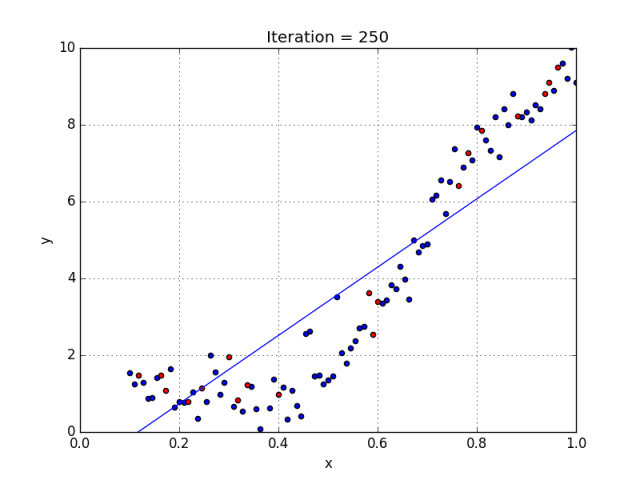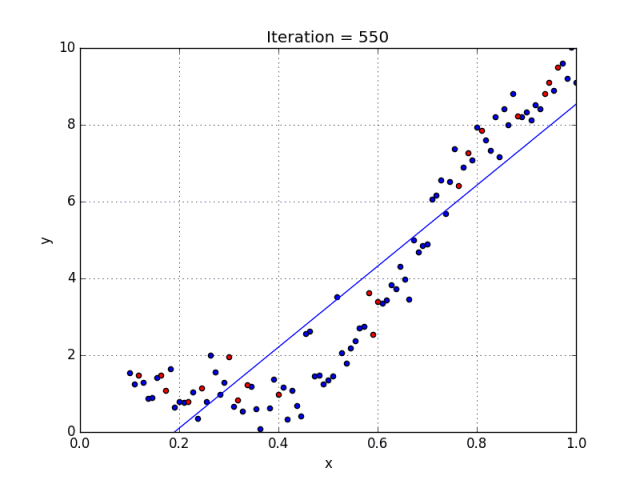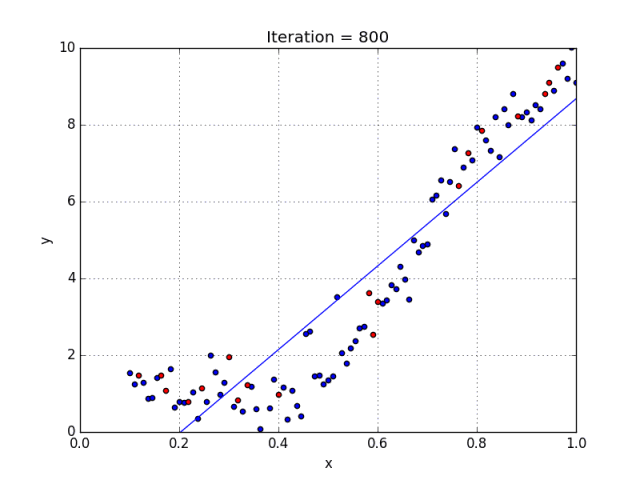
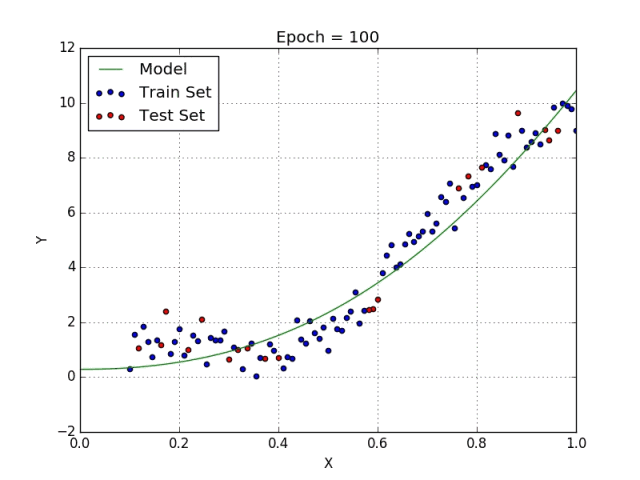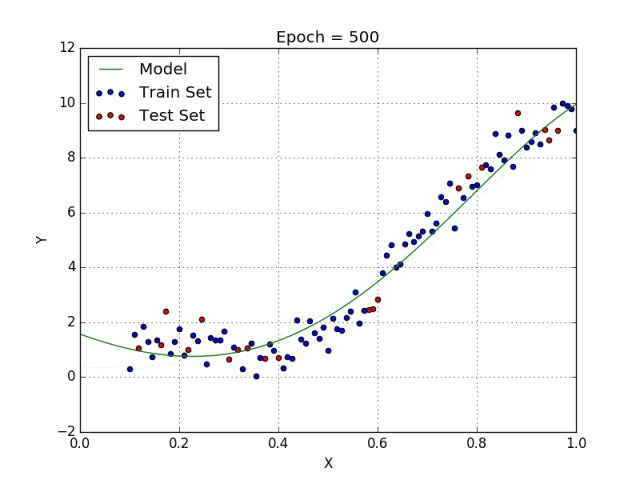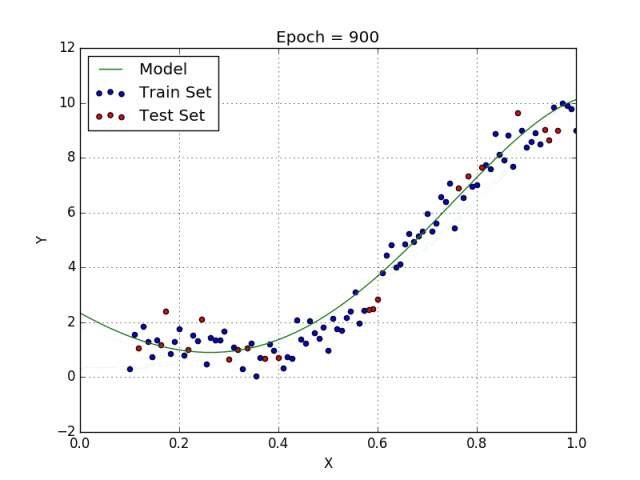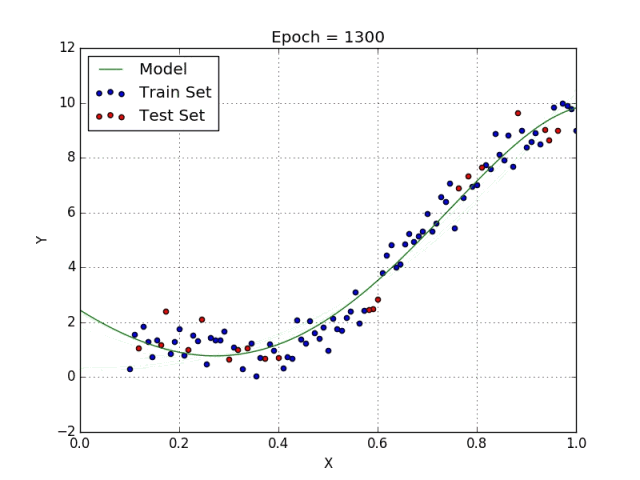
多项式回归的几个要点：

• 能够模拟非线性可分的数据;线性回归不能做到这一点。它总体上更灵活，可以模拟一些相当复杂的关系。

• 完全控制要素变量的建模（要设置变量的指数）。

• 需要仔细的设计。需要一些数据的先验知识才能选择最佳指数。

• 如果指数选择不当，容易过拟合。

岭回归（Ridge Regression）

标准线性或多项式回归在特征变量之间存在很高的共线性（high collinearity）的情况下将失败。共线性是自变量之间存在近似线性关系，会对回归分析带来很大的影响。

我们进行回归分析需要了解每个自变量对因变量的单纯效应， 高共线性就是说自变量间存在某种函数关系，如果你的两个自变量间（X1和X2）存在函数关系，那么X1改变一个单位时，X2也会相应地改变，此时你无法做到固定其他条件，单独考查X1对因变量Y的作用，你所观察到的X1的效应总是混杂了X2的作用，这就造成了分析误差，使得对自变量效应的分析不准确，所以做回归分析时需要排除高共线性的影响。

高共线性的存在可以通过几种不同的方式来确定：

• 尽管从理论上讲，该变量应该与Y高度相关，但回归系数并不显著。

• 添加或删除X特征变量时，回归系数会发生显着变化。

• X特征变量具有较高的成对相关性（pairwise correlations）（检查相关矩阵）。

我们可以首先看一下标准线性回归的优化函数，然后看看岭回归如何解决上述问题的思路：

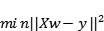
其中X表示特征变量，w表示权重，y表示真实情况。岭回归是缓解模型中回归预测变量之间共线性的一种补救措施。由于共线性，多元回归模型中的一个特征变量可以由其他变量进行线性预测。

为了缓解这个问题，岭回归为变量增加了一个小的平方偏差因子（其实也就是正则项）：

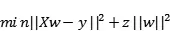
这种平方偏差因子向模型中引入少量偏差，但大大减少了方差。

岭回归的几个要点：

• 这种回归的假设与最小平方回归相同，不同点在于最小平方回归的时候，我们假设数据的误差服从高斯分布使用的是极大似然估计（MLE），在岭回归的时候，由于添加了偏差因子，即w的先验信息，使用的是极大后验估计（MAP）来得到最终参数的。

• 它缩小了系数的值，但没有达到零，这表明没有特征选择功能。

Lasso回归

Lasso回归与岭回归非常相似，因为两种技术都有相同的前提：它们都是在回归优化函数中增加一个偏置项，以减少共线性的影响，从而减少模型方差。然而，不像岭回归那样使用平方偏差，Lasso回归使用绝对值偏差作为正则化项：

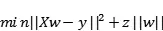
岭回归和Lasso回归之间存在一些差异，基本上可以归结为L2和L1正则化的性质差异：

• 内置的特征选择（Built-in feature selection）：这是L1范数的一个非常有用的属性，而L2范数不具有这种特性。这实际上因为是L1范数倾向于产生稀疏系数。例如，假设模型有100个系数，但其中只有10个系数是非零系数，这实际上是说“其他90个变量对预测目标值没有用处”。 而L2范数产生非稀疏系数，所以没有这个属性。因此，可以说Lasso回归做了一种“参数选择”形式，未被选中的特征变量对整体的权重为0。

• 稀疏性：指矩阵（或向量）中只有极少数条目非零。 L1范数具有产生具有零值或具有很少大系数的非常小值的许多系数的属性。

• 计算效率：L1范数没有解析解，但L2范数有。这使得L2范数的解可以通过计算得到。然而，L1范数的解具有稀疏性，这使得它可以与稀疏算法一起使用，这使得在计算上更有效率。

弹性网络回归（ElasticNet Regression）

ElasticNet是Lasso回归和岭回归技术的混合体。它使用了L1和L2正则化，也达到了两种技术的效果：

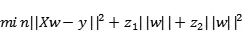
在Lasso和岭回归之间进行权衡的一个实际优势是，它允许Elastic-Net在循环的情况下继承岭回归的一些稳定性。

**ElasticNet回归的几