作者简介

少伟，负责度假起价、搜索的研发工作，资深技术控。

锦涛，负责度假搜索及相关子系统的建设，对搜索引擎、NLP等有浓厚兴趣。

背景介绍

携程度假搜索引擎（以下简称为引擎）：携程度假搜索引擎是一个专注在旅游行业的垂直搜索引擎，用来查找符合从出发地到目的地的相关旅游产品（跟团、自由行、邮轮、游学、主题游等），是一个典型的O2O搜索引擎（Online To Offline）。

本文将分享度假搜索引擎的优化过程及相关思路，希望可以给公司同类项目以及行业同类需求提供一些启发和借鉴。

一、业务特点和难点

主要业务范围： 团队游、自由行、游学、主题游、玩乐门票、邮轮等旅游线路、资源的搜索。

业务特点： 旅游打包类产品包含众多SKU（静态和实时匹配），引发产品状态变更的变量非常多，同时产品可见状态并不都是索引状态直接确定，因此索引的更新频率较高、查询场景复杂。

业务难点： 搜索做为一个流量入口，用户使用是为了寻找合适的产品服务，因此用户的访问体验极为重要。同时不同用户的需求多种多样，因此查询场景非常复杂，在满足不同业务诉求时，需要同时保证用户的查询效率是搜索的难点。

二、名词解释

出发城市： 主要是包含大交通（飞机、动车高铁等）的城市，产品往往会关联多个可出发城市，班期、价格、分数等信息都是和出发城市关联的。

最优出发城市： 根据用户地理位置等信息，从产品可出发城市列表中实时计算当前产品最符合用户的出发城市。最优出发城市用于确定当前产品的价格、班期、分数等等信息。

数据采集系统： 简称DAS，是对搜索引擎依赖的数据源做采集、归并、结构化的一套系统，主要提供三种模式：

  1. 全量：对某一数据源做全量数据采集，一般全量建索引的时候使用；
  2. 增量：对业务方的增量变更做采集，一般都是消费业务方的变更消息；
  3. 批量：对某一类数据做手动补偿（很少使用）。

三、搜索1.0

产品的可出发站点比较少，只有63个，产品结构比较简单，数据量也小，只有10W左右。为了降低产品的检索复杂度，采用了一种冗余的索引结构，每个站一套索引，根据用户的定位信息映射到对应的站点进行检索。

优点： 索引结构简单，检索速度非常快，建立索引时就可确定产品大部分状态；

缺点： 数据冗余，特别是全国出发的产品，在每个站点的索引里面都会建立一套索引。

四、搜索2.0

随着业务的高速发展，原来63个出发站已不满足业务需求，需要扩充到2K+，而且产品也变得更为复杂，数据源更加分散，业务方在数据存储上也变得更加多元（DB,HIVE,HBASE,REDIS,MQ等）。

4.1 主要面对的问题

  1. 2K+出发城市以及众多相关信息该如何建立索引
  2. 数据开始急骤增长
  3. 业务对数据的新鲜度要求更高（分钟级）

4.2 索引的设计和思考

  1. 继续用空间换时间沿用分站点的方式对数据降维，2K+出发站建立2K+索引。

检索友好，但在写入上的开销及空间的占用都不可承受，并且出发站还有进一步扩充的可能。

  1. 父子文档，将产品和出发城市相关信息分开索引，关联查询。

写入友好，但每次计算产品最终态都要关联子文档，开销大、性能差，且复杂的排序很难实现。

最终使用在查询、写入、代码实现上都比较折中的方案——建立宽索引，将每个出发城市相关的数字都存储成一个字段。

4.3 数据采集写入

采用直连的方式写入，数据采集预处理后，直接写入索引，并在HBASE中备份写入。

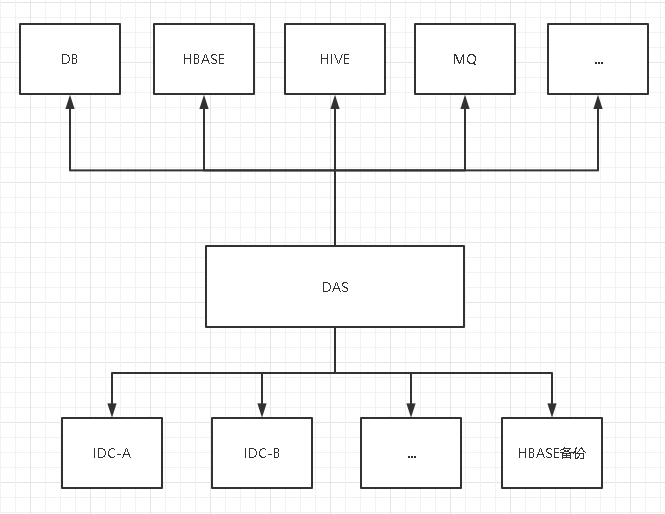
图1 数据采集写入

随着业务进一步发展新出现的问题：

  1. 业务发展太快，仅评分数据就出现了近十种，原本类map多字段的索引方案导致索引字段急骤增加，数据还很稀疏，评分也从原来的2阶（出发站，分）数据增加到3阶（出发站、目的地、分）甚至4阶数据（出发站、目的地、类型、分），原本的索引方案已经无法存储这种高纬度数据。
  2. 直连写入虽然可以更高效的写入数据，但也会导致写入出现高峰波动，而影响到查询，无法很好的调节写入速率。特别是集群出现故障后，补偿数据只能靠全量，每个采集器只采集自己对应业务的数据，一个产品需要写入很多次才能对外可见。

4.4 思考及解决

放弃原来的多字段存储方案，采用一种更加紧凑的存储结构Bit，将多阶数据存放到一个long的不同位段，通过脚本来获取不同的位段在进行计算。

以2阶分数为例，高31位存放出发站，低32位存放具体分值，每个出发城市一条记录，构成一个long数组，建立索引时将数组排序可用二分查找来加快查找速度。

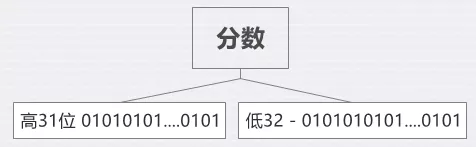
图2 思考及解决

DAS升级，采集和索引写入分开，用消息队列来解耦。

  1. 可以调节写入速率来对写入削峰；
  2. 采集端增加信息聚合能力，当前采集器采集完成后，会传递给下一个采集器继续采集，等所有的采集完成后才发消息，写入由多次变为一次；
  3. 通过消息可以更好的实现多写，以及数据补偿；
  4. 采用双队列，将数据按照重要程度划分队列，避免比较重要的数据排队比较靠后而导致的重要更新迟滞。

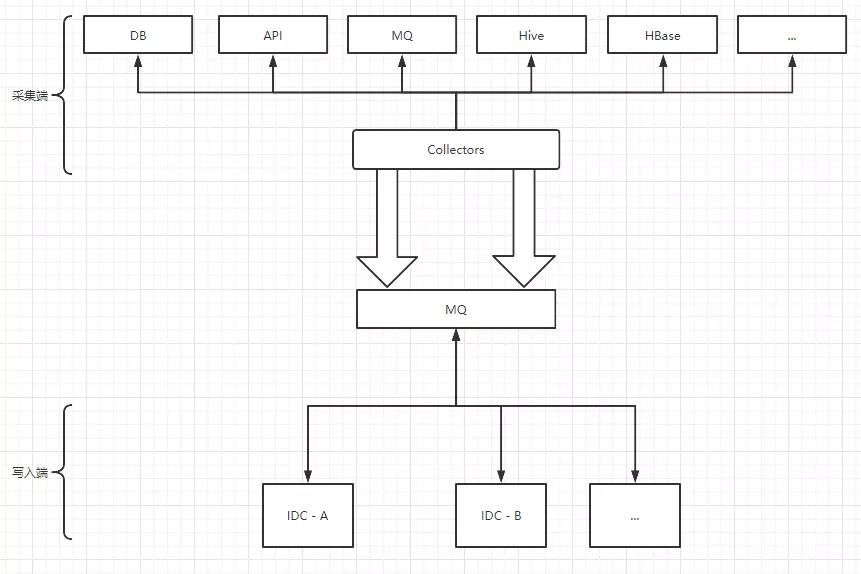
图3 采集和索引写入分开

五、搜索3.0

数据量持续增长，班期增长到8E+，同时为解决搜索2.0中存在的问题，我们进行如下优化。

5.1 索引写入优化

5.1.1 班期写入优化

随着数据量的骤增，原来每2小时全量班期更新给数据处理及ES更新带来了较大的压力，我们通过以下优化来缓解这一情况。

  1. 由每2小时全量写入→每天全量补偿+每5分钟增量更新，单次更新数据量大大减少，更新频率更高，更新更及时；
  2. 使用spark并行处理数据，并写回消息队列；

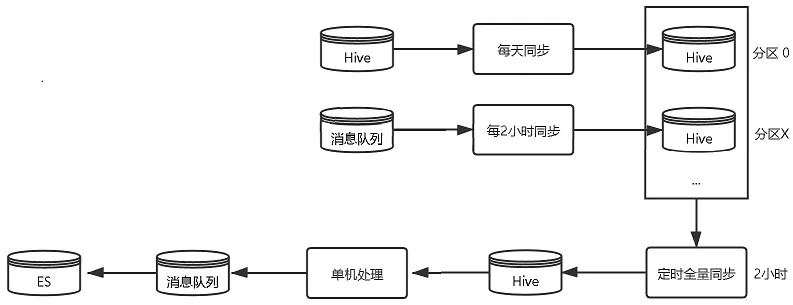
2小时定时同步

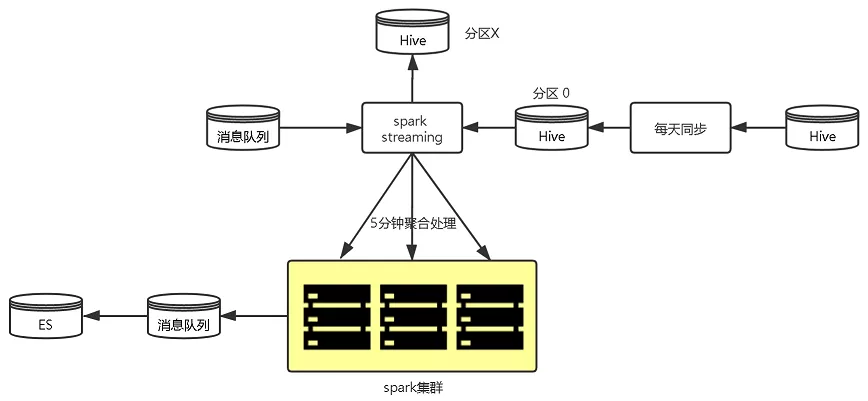
5分钟增量同步

图4 班期写入优化

5.1.2 消息处理优化

上游数据量越来越大，更新越来越频繁，ES的更新压力越来越大，更新的延时不断的升高，导致的业务报修不断上升，为了缓解这个问题，我们做了如下优化：

  1. 把用户感知强的城市上下线状态和价格变更消息区隔开来，城市上下线状态单独队列处理，消息处理量减少为原来的1/10，处理速度快，业务报修大量减少。
  2. 价格变更消息的更新量大，按一定的时间间隔进行聚合处理，消息更新量减少30%，减少对ES的更新压力。

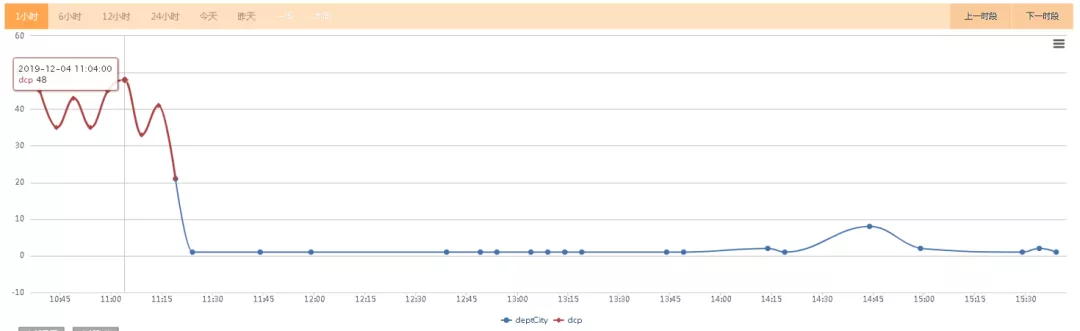
图5 ES写入延迟优化

5.1.3 缓冲式写入

搜索使用的元数据分散在各个业务线上，数据源比较分散，导致写入频次高，更新碎片化，一个产品可能在数分钟内会更新多次。

增量时对于一些更新量比较大，时效性要求不太高的数据，我们采用了缓冲合并写入。

  1. 收到信息变更后并不直接写入MQ而是写入到缓冲区（Redis）；
  2. 缓冲区会将相同的产品信息合并成一条产品（多个不同的节点更新）；
  3. 5分钟定时将缓冲区（redis list）里的产品key取出，并取出对应的redis value，组成一个批量更新，写入索引。

起价等信息写入降低到原来的1/3。

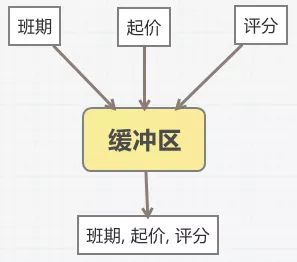
图6 缓冲式写入

5.2 索引结构优化

5.2.1 班期压缩

班期数据一直是搜索ES占用空间最大的一块数据集，占到索引的一半大小，索引存储6个月的数据，极端情况下每个出发站就需要180条记录，且班期数据不光要实现班期筛选，还需要筛选聚合出月份筛选项，极大的影响性能。

一个月最大31天，我们采用一种压缩格式，使用long类型，低的31位标识每天的班期，1代表有，0代表没有，32-35（共4位，最大15）代表月份，36-41（共5位，最大31）代表年份，42-63（共32，最大83888607）代表出发城市，原本一个月31条记录，只需要一条记录，空间压缩到原来的1/31，采用新的索引存储格式大大降低了遍历的深度。

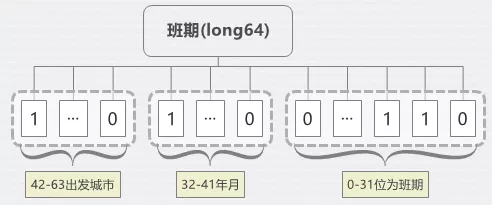
图7 班期压缩

除了班期外，各种打分数据，起价数据等和出发城市相关的数据都采用了类似的数据结构压缩，老结构存储：30W+数据占用100G+，新结构存储：60W左右数据占用不足10G，只相当于老结构的1/15。

5.2.2 字段压缩

原有的索引很多地方使用了map结构，而map结构的每一个值对于ES都会生成一个字段。当出发地随着业务的扩展不断增大的时候，所有跟出发地有关的索引字段在急骤的膨胀，达到了7K+，使用得ES索引的数据非常稀疏，也给索引的更新带来了很大的压力。

因此，我们结合map和array各自的特点，设计了一个新的存储方式：map+array。整体数据存储依然采用array的方式，只是将原来单个array的数据通过出发城市取模后映射进多个字段内，数据计算的时候，不需要对全量数据进行遍历，只需要根据最优出发城市找到对应的array桶在进行遍历即可，避免全局查询。

图8 字段压缩

优点：

  1. 在空间和时间上找到比较好的平衡点
  2. 防止map占用字段过多，弥补了array遍历太慢
  3. 字段的扩充是可以预见的

缺点：

  1. 增加一定的复杂性
  2. 该方案依赖于素数取模，目前取值11，如果后续要更改的话，数据需要全量变更，因此使用此方案要提前做好规划

结果：

  1. 字段数减少，从7K+减少到130+
  2. 原array类型取模后带来查询性能提升，从O(m*n)到O(n+1)，目前m=11

5.3 查询性能优化

我们在线上排查业务问题时，发现部分请求每次搜索产品召回数量都不一样，最终定位下来是查询耗时超过请求设置超时时间，因此出现每次召回产品数量都不一致的情况。排查下来涉及的代码里有两个地方较慢：

  1. 寻找最优出发城市
  2. 寻找出发城市对应的POI分值

针对此种情况，我们做了如下优化：

  1. 寻找最优出发城市的时候，把对list的遍历改为map，那么单次的查询效率就从O(n)到O(1)；
  2. 寻找出发城市对应的POI分值，同样是一个list（出发城市列表×POI个数，假设出发城市列表N，POI个数为M，列表总元素个数为M × N），POI个数我们是事先知道的，原来的查询复杂度为O（M ×N），实际我们可以把数组当成一个二叉树结构来看，那么单次的查询时间复杂度就为O（log2 (M × N))。

POI的个数我们事先是知道的，最终优化下来的时间复杂度为O(M × log2 (M × N)))，优化后的查询性能提升明显，特别是产品数众多，定位小站的长尾访问，耗时降低为原来的1/2（小站出发地基本上靠后，优化完后大站小站的访问响应时间基本