敏感词匹配系统的设计与实践
作者:vivo互联网服务器团队-Liang Kangwu
一、前言
谛听系统是vivo的内容审核平台,保障了vivo各互联网产品持续健康的发展。谛听支持审核多种内容类型,但日常主要审核的内容是文本,下图是一个完整的文本审核流程,包括名单匹配、敏感词匹配、AI机器审核、人工审核四个环节。待审核文本需要顺次通过名单匹配、敏感词匹配、AI机器审核三个流程,若结果为嫌疑则需要人工审核,否则将直接给出确定的结果。
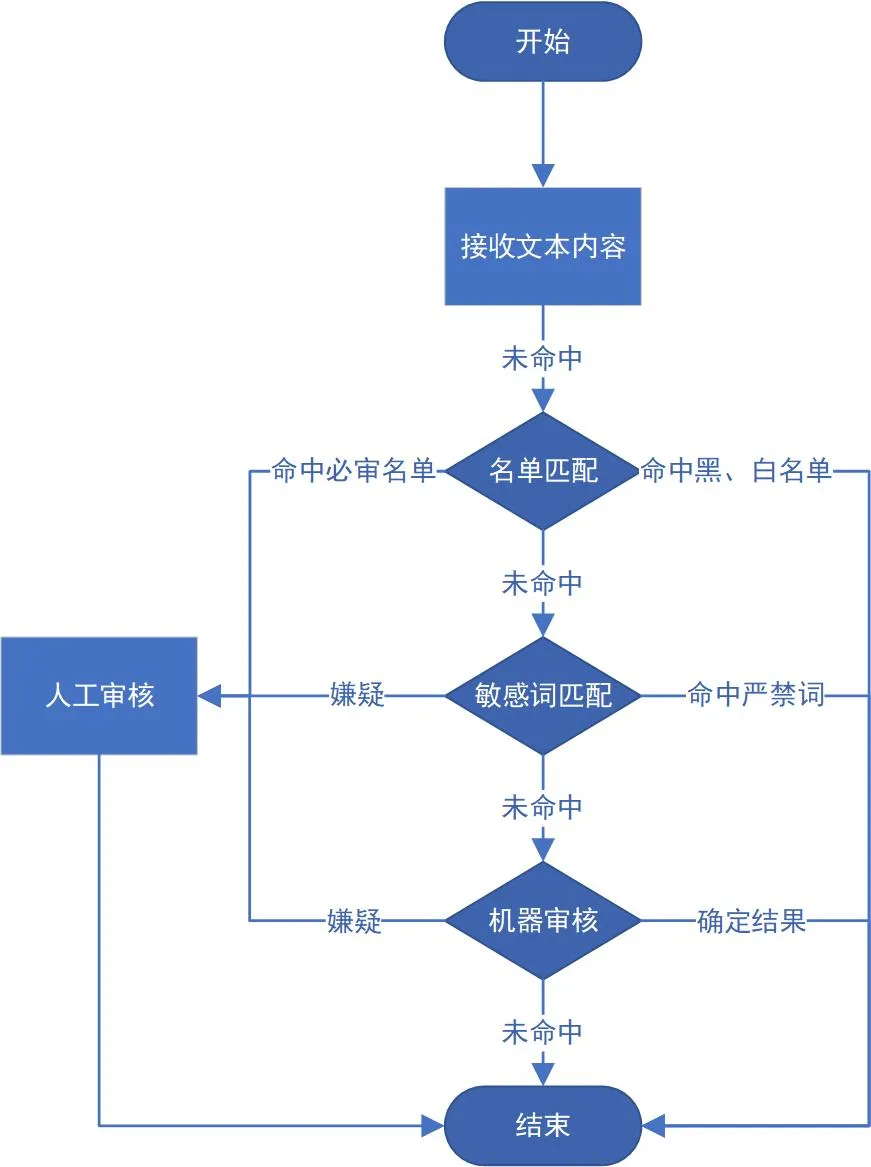
敏感词匹配功能可以迅速地匹配文本中的敏感词汇,算法平均耗时为50ms,因其简单、快速、直接、灵活的特点,成为了审核人员对抗垃圾文本的利器。然而身处信息爆炸时代的网民们非常“优秀”,他们源源不断的发明各种新词、谐音词来绕过敏感词检测。例如某些用户会使用“啋票”、“采漂”等词汇来规避敏感词“彩票”,其中“啋票”不仅是谐音词,还包含多音字,常规的模式匹配算法很难保证完全命中。这不仅给运营规则带来挑战,也对匹配算法的精准度、漏杀率提出了要求。
本文将从算法选型入手,结合两个实际场景来介绍谛听系统的敏感词匹配算法。其中第二节介绍了底层算法选型思路,第三节介绍了两种实际场景下提升敏感词精准度、降低漏杀率的方案。
二、算法选型
敏感词匹配功能依托于模式匹配算法。模式匹配的定义是,给定一个子串,在某个字符串中找出与该子串相同的所有子串。其中给定的子串被称为模式串,被匹配的字符串被称为目标串。基于多个模式串进行匹配的算法被称为多模式匹配算法,目前成熟的多模式匹配算法有AC自动机和WM。
2.1 多模式匹配算法对比
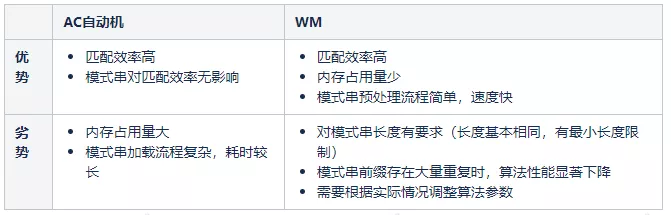
谛听的敏感词匹配业务有如下特点:
1)词库量大,需要维护和加载百万级别的词库(模式串);
2)敏感词与业务特性、国家政策相关性强,无法统一约定长度、前缀等特征。
WM算法对模式串的长度和前缀存在一定的要求,可能会影响业务的使用。虽然AC自动机加载耗时长,内存占用大,但敏感词加载并不频繁,且服务器内存资源充足,所以我们最终选用AC自动机作为底层算法。
2.2 AC自动机算法介绍
AC自动机算法(Aho–Corasick算法)是一种字符串搜索算法,可以同时将目标串与所有模式串进行匹配,算法均摊情况下具有近似于线性的时间复杂度。AC自动机的匹配原理有两个核心概念: Trie字典树、 Fail指针。下面以模式串集合{“she”, “he”, “shers”, “his”, “era”}为例,来介绍这两个概念。
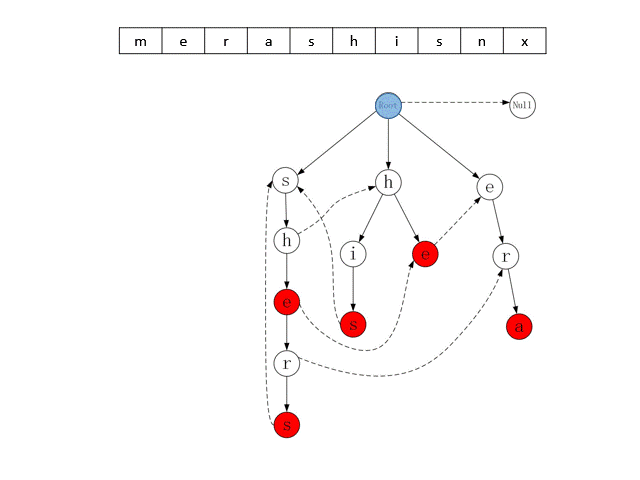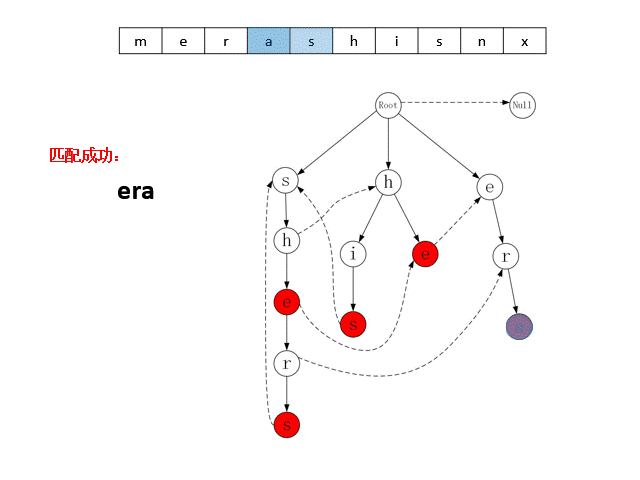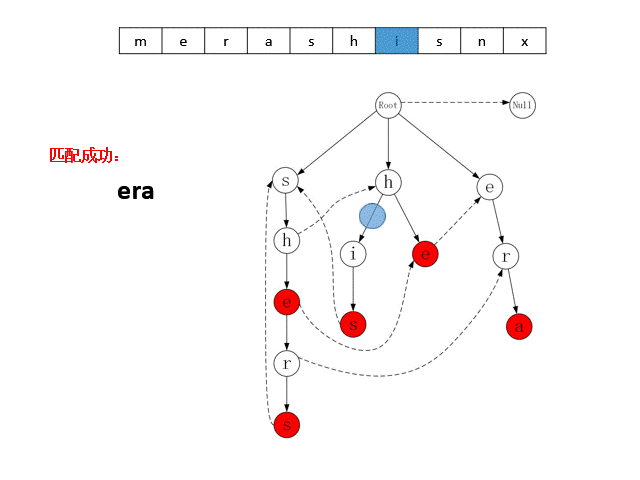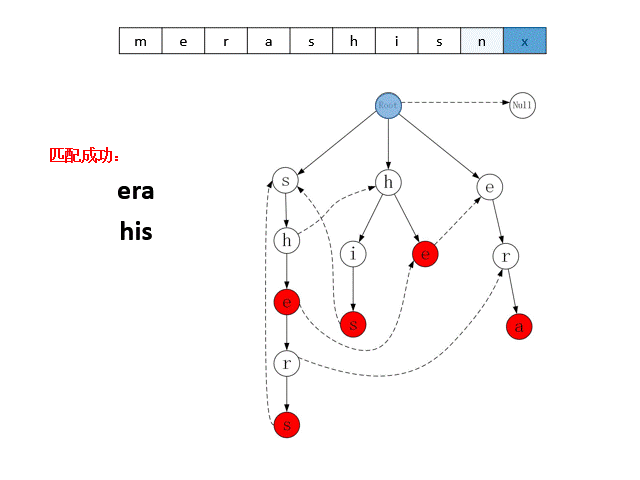
AC自动机算法启动时,需要将所有的模式串加载到内存中,构建成一个Trie字典树。例如下图是以模式串集合**{“she”, “he”, “shers”, “his”, “era”}**构建的字典树,树中每个节点代表一个字符,从根节点到某一个节点的路径,即可表示一个模式串,且红色节点表示一个字符串的终结,例如图中最右边子树上的三个节点,可代表模式串“era”。从字典树的根节点出发,可以快速的查找到某个模式串。此外,拥有相同前缀的模式串会合并到同一个子树中,例如中间子树表示模式串“he”、 “his”,这两个字符串分别是“h”节点的一个分支。AC自动机在搜索这类字符串时,可以节省匹配的次数。
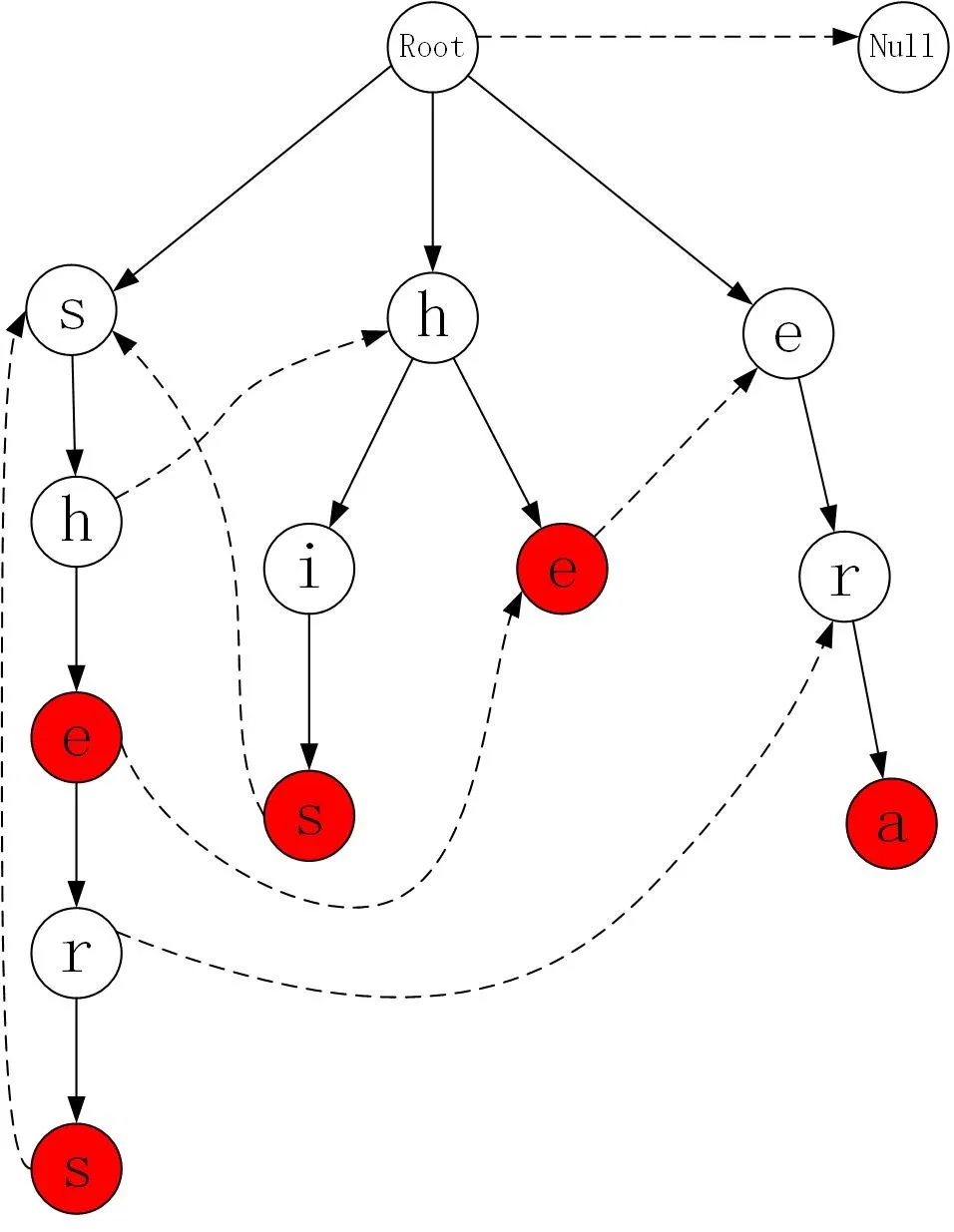
AC自动机在Trie树的基础上,为每个节点加入了 Fail 指针,上图使用虚线画出了部分节点的Fail指针,未画出虚线的节点,其Fail指针指向根节点。算法在某个节点匹配失败时,可以通过该指针转移到其他包含相同前缀的分支上继续匹配。例如匹配目标串“ shis”时,对于前两个字符“ sh”,Trie字典树匹配到左边字数的“ h”节点上,由于该节点的子节点是字符“ e”,与目标串的下一个字符“ i”不匹配,因此算法通过Fail指针转移到中间子树的“h”节点上继续匹配,最终命中字符串“ his”。
上述的 Trie 字典树与Fail指针组成了AC自动机的数据模型。AC自动机匹配目标串时,会按顺序从目标串中取出字符,从Trie字典树的根节点出发,在子结点中寻找与该字符匹配的结点,若能找到,则转移到该节点,若找不到,则转移到Fail指针指向的节点。当状态转移到图中的红色节点时,就是命中了一个模式串。下图展示了AC自动机对目标串“ merashisnx”进行匹配的过程。
三、谛听系统实践
谛听系统基于AC自动机算法构建了一套敏感词匹配服务,将敏感词作为模式串,文本内容作为目标串,可以实现常用的中、英文敏感词匹配。但是实际的业务有很多细分的场景,普通的AC自动机算法已不能满足业务使用需求,因此我们探索了组合敏感词匹配和拼音敏感词匹配两种匹配方式,下面分别介绍。
3.1 组合敏感词
常规的敏感词匹配算法通常匹配单个词或者短句,但某些词单独出现时并不违规,只有在与几个特定的词同时出现时,才能判定为违规。例如“ 澳门”、“ 博彩”、“ 网站”,这几个词,单独出现都是没问题的,但是在这句话中:“ 欢迎登录澳门XX博彩官方网站”,就是违规的赌博广告。针对这样的场景,我们实现了“组合敏感词”匹配方案,运营人员可以将这几个词配置成一个组合“ 澳门+博彩+网 站”,只有这三个词同时出现时,敏感词服务才会判定这个组合命中。
组合敏感词的匹配算法依然基于AC自动机算法。由于AC自动机只能判断单个词的命中情况,因此我们将组合敏感词分割成单个敏感词,并维护各敏感词与组合间的映射关系,在AC自动机算法运行结束后,只有某个组合对应的敏感词全部命中时,才能判断该组合敏感词命中。为此我们需要给AC自动机添加一些前置和后置的处理步骤,具体步骤如下:
- 将组合敏感词分割为单个敏感词,并记录敏感词与组合的映射关系;
- 将分割后的组合敏感词添加到AC自动机的Tire树中;
- 运行AC自动机,匹配文本;
- 遍历匹配结果,将匹配的结果根据映射关系映射到相应的组合上;
- 记录组合的命中情况,得到最终匹配结果。

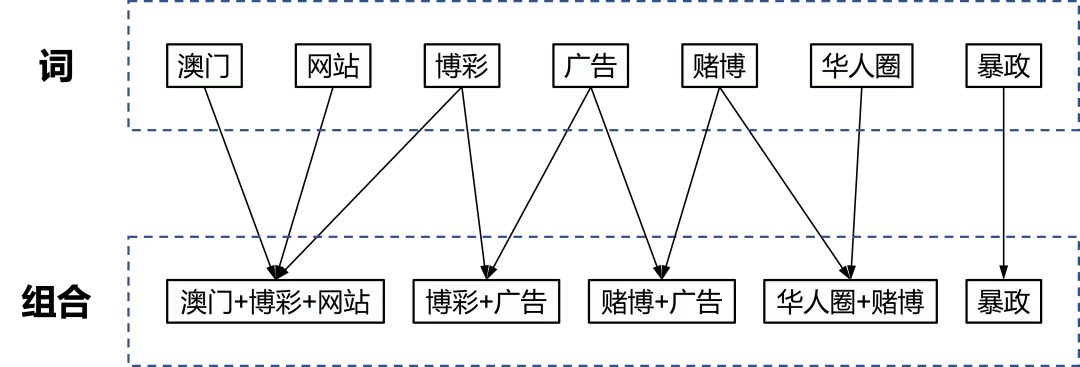
假设目前存在组合敏感词“ 澳门+博彩+网站”、“ 博彩+广告”、“ 华人圈+赌博”、“ 赌博+广告”,以及普通敏感词“ 暴政”,则在步骤1中,我们将组合敏感词分割为单个敏感词:“ 澳门”、“ 网站”、“ 博彩”、“ 广告”、“ 赌博”、“ 华人圈”、“ 暴政”,并建立图中所示的映射关系。将这些词添加到AC自动机后,对文本“ 欢迎登录澳门XX博彩官方网站”进行匹配时,会命中单个敏感词“ 澳门”、“ 网站”、“ 博 彩”。在步骤4中,算法将匹配的词映射到组合中,并标记对应的词命中。例如根据“ 博彩”,可取到组合“ 澳门+博彩+网站”、“ 博彩+广告”,则分别标记这两个组合中的“ 博彩”已命中。步骤5会根据各组合中单词的命中情况,来判断该组合是否命中,由于在步骤4中组合敏感词“ 澳门+博彩+网站”的三个词均被标记为命中,因此可判断该组合命中。
3.2 拼音敏感词
在评论、弹幕等创作自由度很高的场景中,某些用户为了规避机器审核,会使用一些多音字、同音字来表达敏感词汇,例如用“啋票”来代表“ 彩票”等。由于多音字、同音字变化较多,将一个词的所有谐音词都穷举出来是很困难的。因此我们实现了拼音敏感词的匹配方案,将中文文本转换为拼音再匹配,通过读音匹配敏感词,即可保证命中所有的同音字,运营直接配置敏感词的拼音,例如“ CAI PIAO”,即可命中“ 啋票”、“ 彩票”、“ 采漂”等词汇。
3.2.1 匹配流程
常规的AC自动机算法是逐字符匹配的,因此Trie树上每个节点存储一个字符,但拼音敏感词需要按照音节匹配,因此我们将Trie树的节点数据类型由char改为String,示例:
拼音敏感词的匹配关键在于将汉字准确的转换为拼音,这一点在多音字的场景下尤为重要。由于多音字的读音是受语境影响的,现有的技术条件很难确保能将多音字准确的转换为拼音,而上文提到同音词“啋票”是用户自行造的词,算法无法准确的识别语境,可能转换得到“ CAI PIAO”、“ XIAO PIAO”两种不同的结果。如果拼音转换不精准,则拼音敏感词也无法准确命中。
因此我们不依赖算法识别多音字的读音,而是将文本内容的所有读音都列出来匹配一遍,就可以避免避免拼音转换不精准的问题。
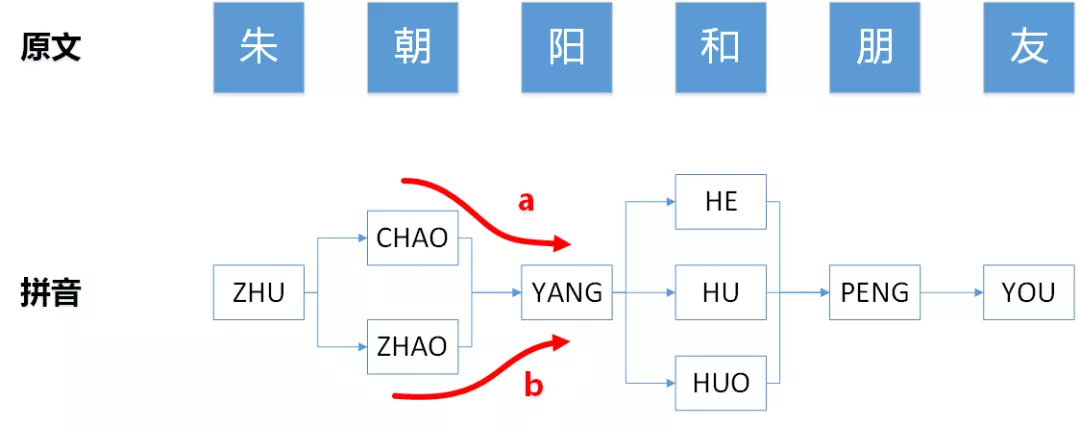
下图展示了文本内容与拼音的对应关系,由于存在多音字,因此存储拼音的数组从一维扩展到了二维,更像是“图”的数据结构,下文将其称为拼音图。拼音图的起始节点和终止节点之间存在多条路径,这些路径对应了多音字的所有排列组合情况,为了避免漏杀,我们需要使用AC自动机将这些路径都匹配一遍。
从第二节的匹配流程可以看出,目标串是一维数组,因此AC自动机在匹配文本时,通常采用顺序遍历的方式。而在拼音敏感词中,由于目标串采用二维数组存储,是一种类似于“图”的数据结构,不再适合使用顺序遍历的方式,因此需要采用图的遍历算法。
图的遍历算法中,最常用的就是深度优先遍历(DFS)和广度优先遍历(BFS)。由于词语是前后关联的,为了使算法更符合人类思考习惯,我们选择了DFS。DFS算法使用栈存储节点信息,在当前分支遍历完成后,通过栈中的信息回溯到上一个分支处继续遍历。由于Trie树的状态位与拼音图的节点是相关的,在DFS回溯时,Trie树也需要同步回溯,因此需要将Trie树状态位与拼音图的节点信息一起保存到DFS栈中。下图展示了拼音敏感词的匹配流程。
3.2.2 终止条件与剪枝策略
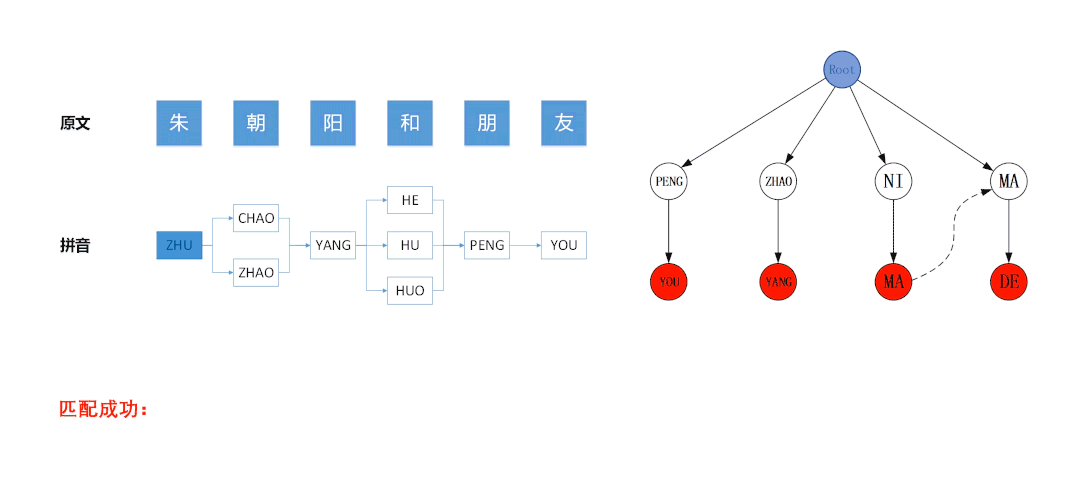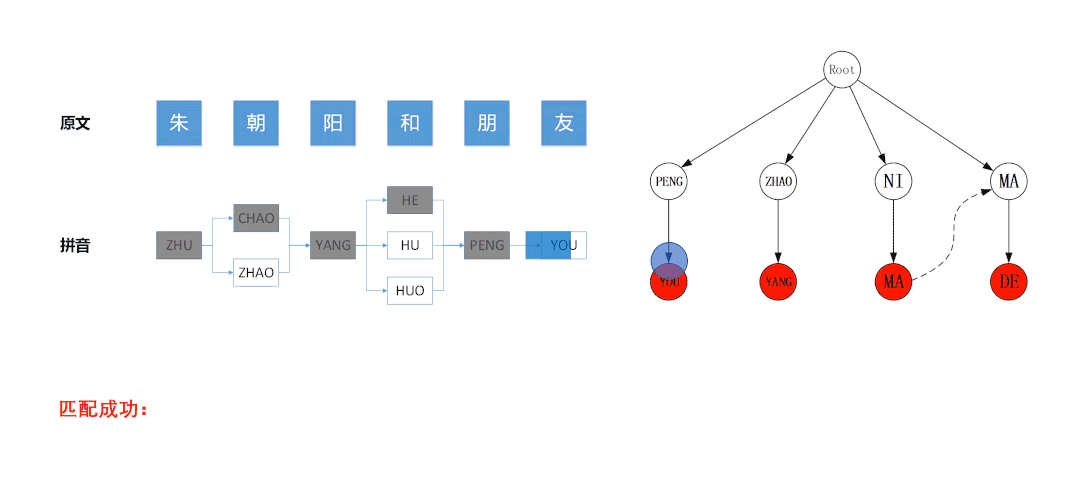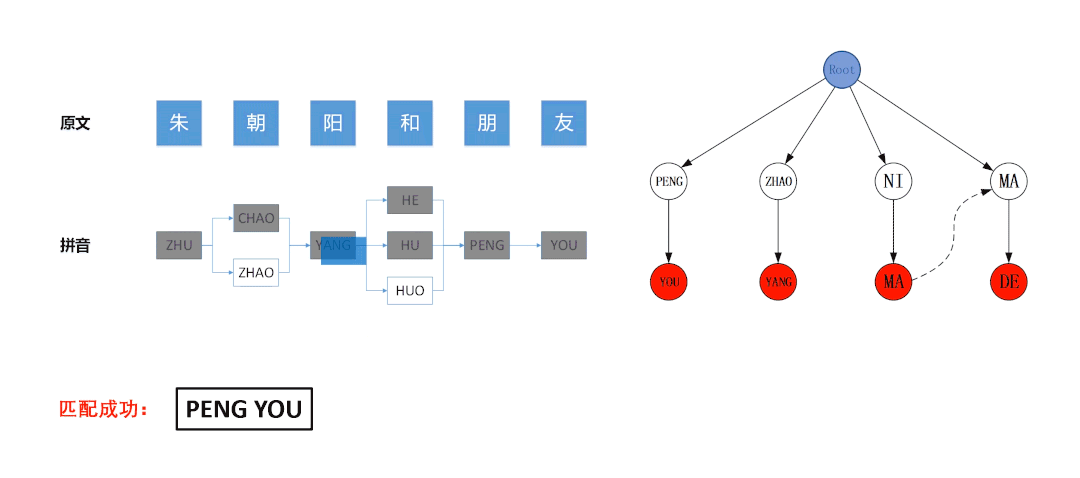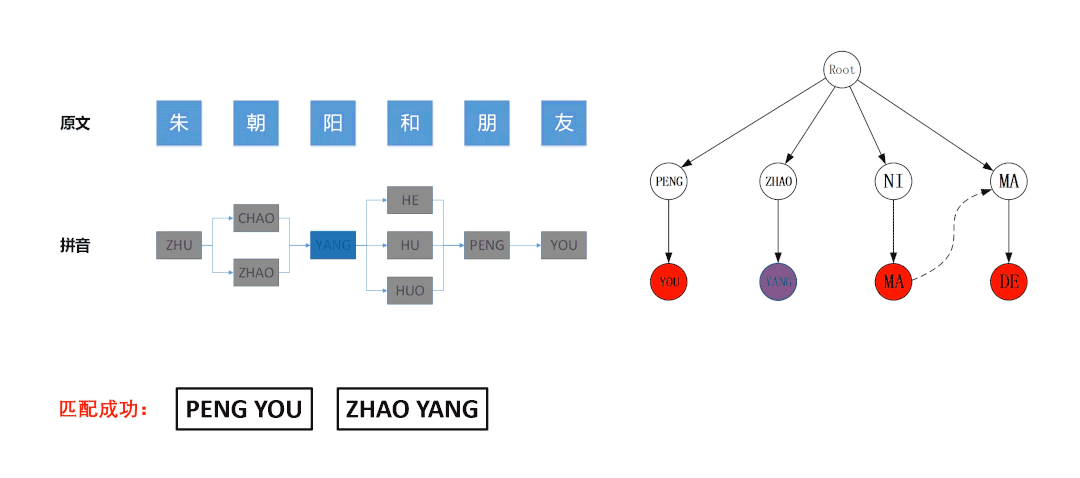
DFS的终止条件是当所有节点都被遍历过,且算法会确保每个节点只会被遍历一次。但是DFS遍历时会在分支处回溯,所以往往终止的节点并不是待匹配文本的终点,很有可能AC自动机的匹配并未完成。
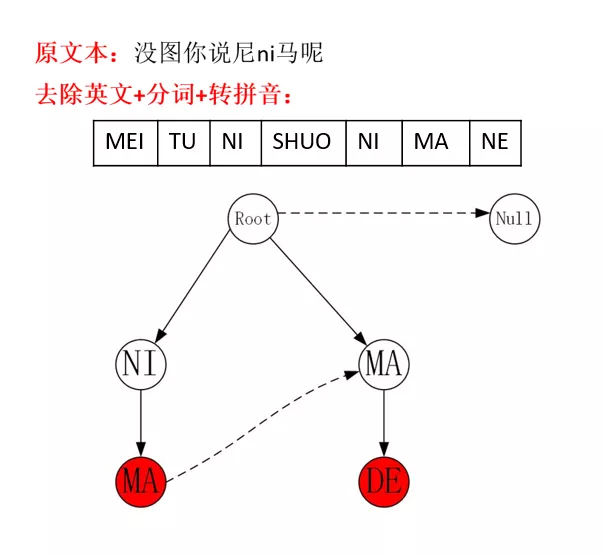
例如在下图所示的匹配流程中,左图是基于待匹配文本“朱朝阳和朋友”构建的拼音图,右图是基于拼音敏感词“PENG YOU”、“ZHAO YANG”、“NI MA”、“MA DE”构建的Trie树。左图的拼音图采用DFS算法遍历,算法最后访问的节点是蓝色节点“ ZHAO”,此时拼音图中所有节点均被遍历了一次,已经达到了DFS的终�
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/%E4%BA%92%E8%81%94%E7%BD%91/%E6%95%8F%E6%84%9F%E8%AF%8D%E5%8C%B9%E9%85%8D%E7%B3%BB%E7%BB%9F%E7%9A%84%E8%AE%BE%E8%AE%A1%E4%B8%8E%E5%AE%9E%E8%B7%B5/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


