腾讯技术数据分析利器算法最佳解析
作者:熊先明,腾讯 CDG 应用研究员
XGBoost是一种经典的集成式提升算法框架,具有训练效率高、预测效果好、可控参数多、使用方便等特性,是大数据分析领域的一柄利器。在实际业务中,XGBoost经常被运用于用户行为预判、用户标签预测、用户信用评分等项目中。XGBoost算法框架涉及到比较多数学公式和优化技巧,比较难懂,容易出现一知半解的情况。由于XGBoost在数据分析领域实在是太经典、太常用,最近带着敬畏之心,对陈天奇博士的Paper和XGBoost官网重新学习了一下,基于此,本文对XGBoost算法的来龙去脉进行小结。
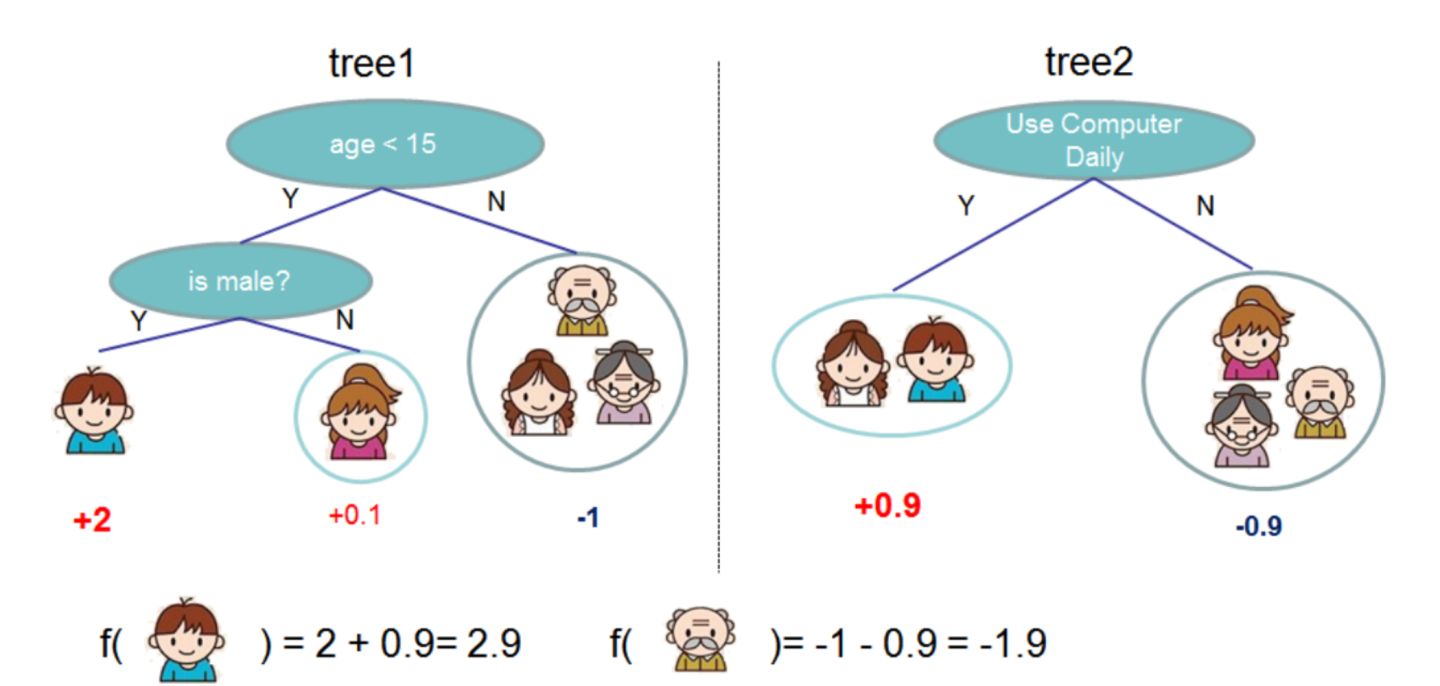
本文重点解析XGBoost算法框架的原理,希望通过本文能够洞悉XGBoost核心算法的来龙去脉。对于XGBoost算法,最先想到的是Boosting算法。Boosting提升算法是一种有效且被广泛使用的模型训练算法,XGBoost也是基于Boosting来实现。Boosting算法思想是对弱分类器基础上不断改进提升,并将这些分类器集成在一起,形成一个强分类器。简而言之,XGBoost算法可以说是一种集成式提升算法,是将许多基础模型集成在一起,形成一个很强的模型。这里的基础模型可以是分类与回归决策树CART(Classification and Regression Trees),也可以是线性模型。如果基础模型是CART树(如图1所示),比如第1颗决策树tree1预测左下角男孩的值为+2,对于第1颗决策树遗留下来的剩余部分,使用第2颗决策树预测值为+0.9,则对男孩的总预测值为2+0.9=2.9。
 XGBoost算法框架可以分为四个阶段来理解(如图2所示)。 第一个阶段,如何构造目标函数? 在进行优化求解时,首先需要构造目标函数,有了目标函数才能进行优化求解。这种思路和LR模型(Logistic Regression)是一致。在LR模型中,首先,对于回归问题构造平方项损失,对于分类问题构造最大似然损失作为目标函数,然后基于构造好的目标函数,才会考虑采用梯度下降算法进行优化求解,比如随机梯度下降、Mini-Batch批量梯度下降、梯度下降等。在这个阶段,我们可以得到XGBoost的基本目标函数结构。
XGBoost算法框架可以分为四个阶段来理解(如图2所示)。 第一个阶段,如何构造目标函数? 在进行优化求解时,首先需要构造目标函数,有了目标函数才能进行优化求解。这种思路和LR模型(Logistic Regression)是一致。在LR模型中,首先,对于回归问题构造平方项损失,对于分类问题构造最大似然损失作为目标函数,然后基于构造好的目标函数,才会考虑采用梯度下降算法进行优化求解,比如随机梯度下降、Mini-Batch批量梯度下降、梯度下降等。在这个阶段,我们可以得到XGBoost的基本目标函数结构。
第二个阶段,目标函数优化求解困难,如何对目标函数近似转换? 在第一个阶段得到的基本目标函数较为复杂,不是凸函数,没法使用连续性变量对目标函数直接优化求极值。因此,使用泰勒级数对目标函数进行展开,对目标函数规整、重组后,将目标函数转换为 关于预测残差的多项式函数。
第三个阶段,如何将树的结构引入到目标函数中? 第二个阶段得到的多项式目标函数是一个复合函数。被预测的残差和模型复杂度还是未知的函数,需要对这两个函数进行参数化表示,即将决策树的结构信息通过数学符号表示出来。在第三个阶段,在树的形状确定情况下,可以优化求解出局部最优解。
第四个阶段,如何确定树的形状,要不要使用贪心算法? 如何在模型空间里面寻找最优的决策树形状,这是一个NP-Hard问题,我们很难对可能存在的树结构全部罗列出来,尤其在特征个数很多情况下。因此,在这里需要使用贪心算法来求得局部最优解。

1.如何构造目标函数?
当使用多棵树来预测时,假设已经训练了



在公式1中,











如果要训练得到






公式2的第二部分表示正则项,是用来控制模型的复杂度,模型越复杂,惩罚力度越大,从而提升模型的泛化能力,因为越复杂的模型越容易过拟合。XGBoost的正则化思路跟






在损失函数中










 对于样本
对于样本









根据XGBoost的递推训练过程,每棵决策树训练时会得到样本对应的预测值,根据样本预测值和真实值比较,可以计算得到模型预测损失值。又因为训练所得的每棵决策树都有对应的结构信息,因此可以得到每棵决策树的复杂度


在公式3中,










2.目标函数优化困难,如何对函数近似转换?
在公式4中,已经得到了需要优化的目标函数,这个目标函数已经是简化后的函数。对于公式4,没法进行进一步优化。为了解决目标函数无法进行进一步优化, XGBoost原文是使用泰勒级数展开式技术对目标函数进行近似转换,即使用函数的1阶、2阶、3阶…


令





在训练第

















3.如何将树结构引入到目标函数中?
接下来的问题是如何对函数










 对于第
对于第



























对于 模型复杂度,










将









基于公式8,对目标函数关于



将等式9带入到公式8中,计算得到树的目标损失值(如等式10),该等式表示决策树损失分数


4.如何确定树的形状?
这里需要注意到一点, 树的叶子节点最优解




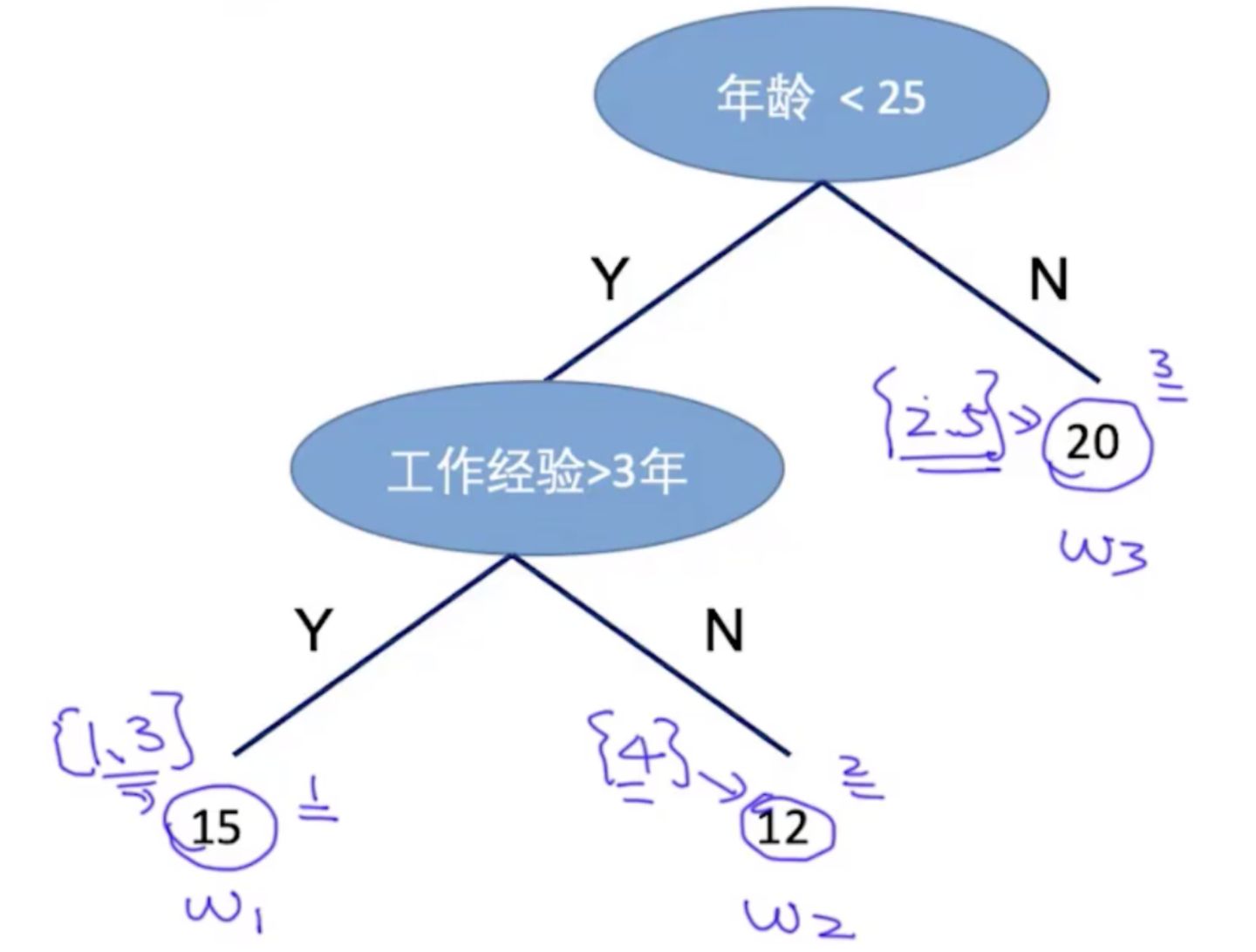
为了寻找树的形状,我们一般使用贪心算法来简化计算,降低计算的复杂度。贪心算法是在局部寻找最优解,在每一步迭代时,选择能使当前局部最优的方向。XGBoost寻找树的形状的思路和传统决策树模型建立树的思路一致。比如传统决策树在进行节点分割时,基于信息熵,选择信息熵下降最大的特征进行分割;对于XGBoost树模型,基于损失函数,选择能让损失函数下降最多的特征进行分割。如图5所示,虚线框是已经构造好的树形状,如果需要在蓝色节点做进一步分裂,此时需要按照某种标准,选择最好的特征进行分割。在这里,XGBoost使用损失函数下降最大的特征作为节点分裂。
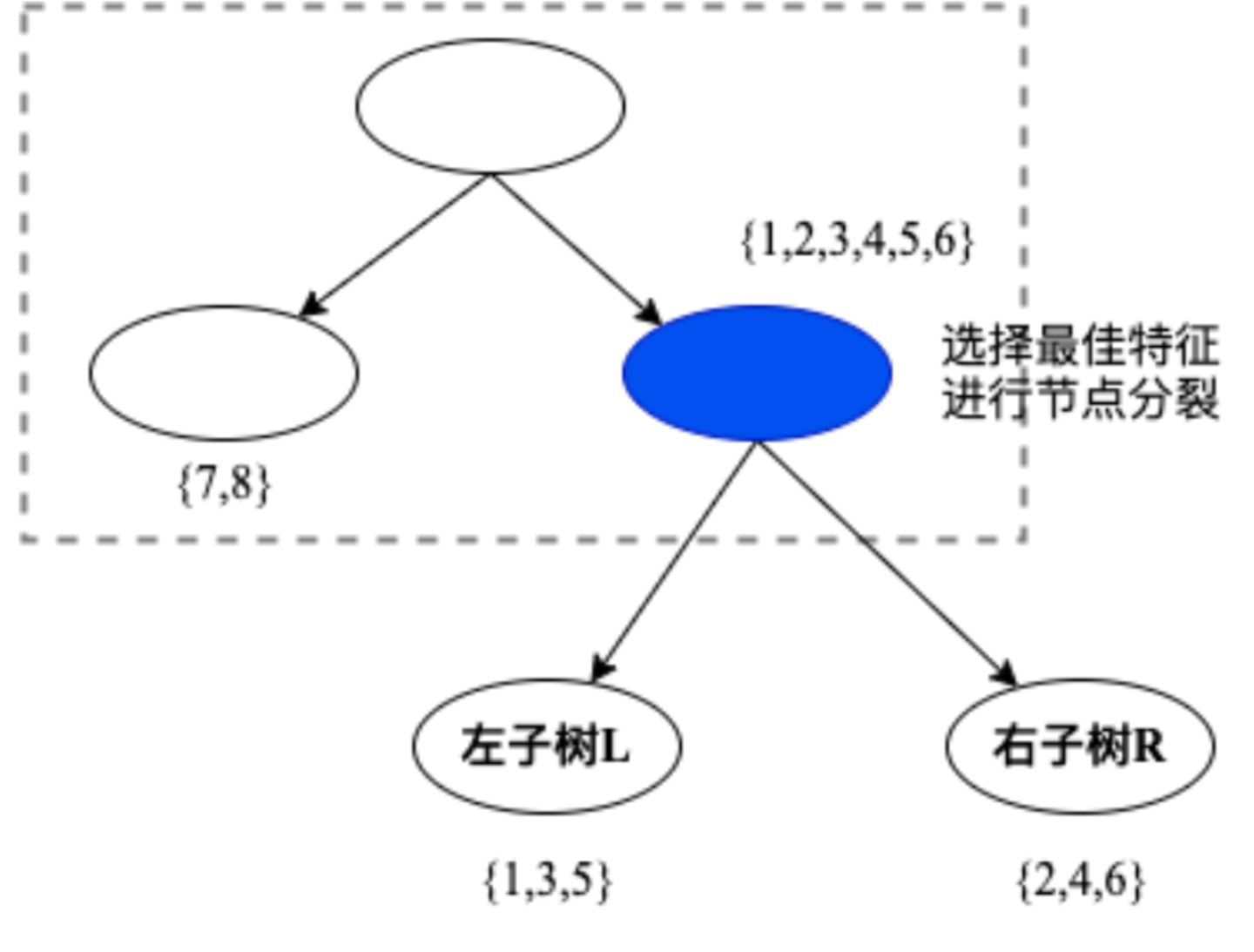 根据公式10,可以计算到蓝色节点在分裂前和分裂后的的损失函数值:
根据公式10,可以计算到蓝色节点在分裂前和分裂后的的损失函数值:





5.其它常见问题
关于XGBoost的常见经典问题,这类问题对于深入理解XGBoost模型很重要,因此,本文对此也进行了梳理小结。
(1) XGBoost为什么需要对目标函数进行泰勒展开?
根据XGBoost官网(如图6所示),目标损失函数之间存在较大的差别,比如平方损失函数、逻辑损失函数等。对目标函数进行泰勒展开,就是为了统一目标函数的形式,针对回归和分类问题,使得平方损失或逻辑损失函数优化求解,可以共用同一套算法框架及工程代码。另外,对目标函数进行泰勒展开,可以使得XGBoost支持自定义损失函数,只需要新的损失函数二阶可导即可,从而 提升算法框架的扩展性。
 相对于GBDT的一阶泰勒展开,XGBoost采用二阶泰勒展开,可以更精准的逼近真实的损失函数, 提升算法框架的精准性。另外,一阶导数描述梯度的变化方向,二阶导数可以描述梯度变化方向是如何变化的,利用二阶导数信息更容易找到极值点。因此,基于二阶导数信息能够让梯度收敛的更快,类似于牛顿法比SGD收敛更快。
相对于GBDT的一阶泰勒展开,XGBoost采用二阶泰勒展开,可以更精准的逼近真实的损失函数, 提升算法框架的精准性。另外,一阶导数描述梯度的变化方向,二阶导数可以描述梯度变化方向是如何变化的,利用二阶导数信息更容易找到极值点。因此,基于二阶导数信息能够让梯度收敛的更快,类似于牛顿法比SGD收敛更快。
(2) XGBoost如何进行采样?
XGBoost算法框架,参考随机森林的Bagging方法,支持样本采样和特征采样。由于XGBoost里没有交代是有放回采样,认为这里的样本采样和特征采样都是无放回采样。每次训练时,对数据集采样,可以增加树的多样性,降低模型过拟合的风险。另外,对数据集采样还能减少计算,加快模型的训练速度。在降低过拟合风险中,对特征采样比对样本采样的效果更显著。
样本采样(如图7所示),默认是

 特征采样(如图8所示),默认
特征采样(如图8所示),默认


(3)XGBoost为什么训练会比较快?
XGBoost训练速度快,这个主要是工程实现优化的结果,具体的优化措施如下几点: 第一、支持并行化训练。XGBoost的并行,并不是说每棵树可以并行训练,XGBoost本质上仍然采用Boosting思想,每棵树训练前需要等前面的树训练完成后才能开始训练。XGBoost的并行,指的是 特征维度的并行。在训练之前,每个特征按特征值大小对样本进行预排序,并存储为Block结构(如图8所示),在后面查找特征分割点时可以重复使用,而且特征已经被存储为一个个Block结构,那么在寻找每个特征的最佳分割点时,可以利用多线程对每个Block并行计算。
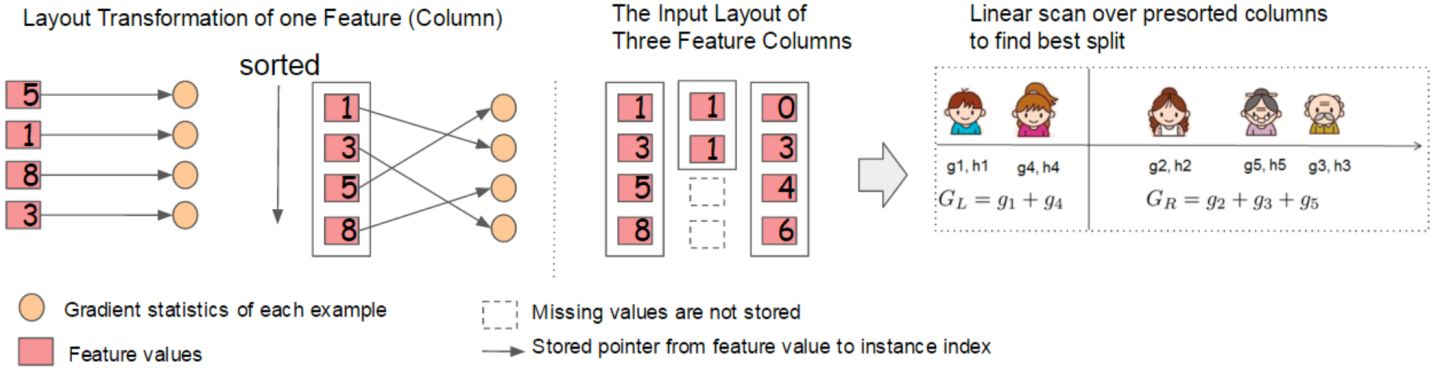 第二、采用近似算法技术,得到候选分位点。在构造决策树分裂节点时,当采用 精确贪心算法 穷举计算每个特征下的所有特征值增益,如果特征个数多、特征取值大,会造成较大的计算量。当样本数据量大时,特征值无法完全加载到内存中,计算效率低。对于分布式数据集,同样会面临无法将特征值全部加载到本地内存的问题。因此,基于这两个现实问题,采用 近似直方图算法,将每个特征取值划分为常数个分位点,作为候选分割点,从中选择相对最优的分割点作为决策树分裂节点。
第二、采用近似算法技术,得到候选分位点。在构造决策树分裂节点时,当采用 精确贪心算法 穷举计算每个特征下的所有特征值增益,如果特征个数多、特征取值大,会造成较大的计算量。当样本数据量大时,特征值无法完全加载到内存中,计算效率低。对于分布式数据集,同样会面临无法将特征值全部加载到本地内存的问题。因此,基于这两个现实问题,采用 近似直方图算法,将每个特征取值划分为常数个分位点,作为候选分割点,从中选择相对最优的分割点作为决策树分裂节点。
第三、缓存感知访问技术。对于有大量数据或者说分布式系统来说,不可能将所有的数据都放进内存里面。因此,需要将其放在外存上或者将数据分布式存储。但是会有一个问题,这样做每次都要从外存上读取数据到内存,这将会是十分耗时的操作。在XGBoost中,采用预读取的方式, 将下一块将要读取的数据预先放进内存里面。这个过程是多开了一个线程,该线程与训练的线程独立并负责数据读取。此外,还要考虑Block的大小问题。如果设置最大的Block来存储所有样本在

第四、Blocks核外计算优化技术。为了高效使用系统资源,对于机器资源,除了CPU和内存外,磁盘空间也可以利用起来处理数据。为了实现这个功能,XGBoost在模型训练时,会将数据分成多个块并将每个块存储在磁盘上。在计算过程中,使用独立的线程将Block预提取到主内存缓冲区,这样数据计算和磁盘读取可以同步进行,但由于IO非常耗时,所以还采用了两种技术来改进这种核外计算。
- Block Compression:块压缩,并且加载到主内存时由独立的线程进行解压缩。
- Block Sharding:块分片,即将数据分片到多个磁盘,为每个磁盘分配一个线程,将数据提取到内存缓冲区,然后每次训练线程的时候交替地从每个缓冲区读取数据,有助于在多个磁盘可用时,增加读取的吞吐量。
除了这些技术,XGBoost的特征采样技术也可以提升计算效率。如果设定特征采样比例colsample_by* < 1.0,则在选择最佳特征分割点作为分裂节点时,特征候选集变小,挑选最佳特征分割点时计算量降低。
(4)XGBoost如何处理缺失值问题?
XGBoost的一个优点是允许特征存在缺失值。对缺失值的处理方式如图9所示: 在特征

在逻辑实现上,为了保证完备性,会将该特征值missing的样本分别分配到左叶子节点和右叶子节点,两种情形都计算一遍后,选择分裂后增益最大的那个方向(左分支或是右分支),作为预测时特征值缺失样本的默认分支方向。 如果在训练中没有缺失值而在预测中出现缺失,那么会自动将缺失值的划分方向放到右子节点。

(5)XGBoost和GBDT的区别是什么?
XGBoost和GBDT都是基于Boosting思想实现。XGBoost可以认为是在GBDT基础上的扩展。两者的主要不同如下: 基分类器:GBDT是以分类与回归决策树CART作为基分类器,XGBoost的基分类器不仅支持CART决策树,还支持线性分类器,此时XGBoost相当于带L1和L2正则化项的Logistic回归(分类问题)或者线性回归(回归问题)。 导数信息:GBDT在优化求解时,只是用到一阶导数信息,XGBoost对代价函数做了二阶泰勒展开,同时用到一阶和二阶导数信息。另外,XGBoost工具支持自定义代价函数,只要函数可以一阶和二阶求导即可。 正则项:XGBoost在代价函数里加入正则项,用于控制模型的复杂度。正则项里包含了树的叶子节点个数、每个叶子节点上输出的预测值的

(6)如何使用XGBoost进行模型训练?
在使用XGBoost前,可以根据官网说明文档进行安装(下面有链接,这里不赘述)。本文采用的数据集是Kaggle平台房价预测开源数据集(地址如参考文章8所示)。值得说明的一点,在进行模型训练前,一般需要做数据清洗、特征工程、样本划分、模型参数调优这些过程。针对这些过程,本文在这里不展开细讲。在进行模型训练前,本文已经完成数据清洗、特征工程、模型参数调优过程,并得到最终用于模型训练的样本集和最优模型参数。如下代码,是使用XGBoost进行模型训练过程。
|
|
6.小结
本文从目标函数构建、目标函数优化、树结构信息表示、树形状确定等四部分,对XGBoost算法框架进行解析。最后,针对XGBoost的常见问题进行小结。通过本文,洞悉XGBoost框架的底层算法原理。在用户行为预判、用户标签预测、用户信用评分等数据分析业务中,经常会使用到XGBoost算法框架。如果对XGBoost算法原理理解透彻,在实际业务中的模型训练过程中,有利于较好地理解模型参数,对模型调参过程帮助较大。
对于文章中表述不妥的地方,欢迎私信于我。
参考文章
(1).陈天奇XGBoost算法原著: https://dl.acm.org/doi/pdf/10.1145/2939672.2939785 (2).20道XGBoost面试题: https://cloud.tencent.com/developer/article/1500914 (3).XGBoost框架Parameters含义: https://xgboost.readthedocs.io/en/latest/parameter.html (4).XGBoost提升树官方介绍: https://xgboost.readthedocs.io/en/latest/tutorials/model.html (5).XGBoost官方论坛: https://discuss.xgboost.ai/ (6).GBDT提升树官方介绍: https://scikit-learn.org/stable/modules/ensemble.html#gradient-tree-boosting (7).XGBoost安装官网说明: [https://xgboost.readthedocs.io/en/latest/build.html](https://zshipu.com/t?url=https%3A%2
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/%E4%BA%92%E8%81%94%E7%BD%91/%E8%85%BE%E8%AE%AF%E6%8A%80%E6%9C%AF%E6%95%B0%E6%8D%AE%E5%88%86%E6%9E%90%E5%88%A9%E5%99%A8%E7%AE%97%E6%B3%95%E6%9C%80%E4%BD%B3%E8%A7%A3%E6%9E%90/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


