详解图表示学习经典算法
16KDD node2vec

node2vec 是斯坦福男神教授 Jure Leskovec 的代表作之一,网上有非常多关于这篇论文的讨论和解析,所以这里我不再累述。
node2vec 中提出的网络的 “ 同质性” 和 “ 结构性” 是两个比较抽象的概念,之前看论文的时候没有仔细斟酌,但看了王喆大佬的文章之后,惊觉一直以来对 node2vec 理解有误。为了搞清楚这两个概念,我写了一份简单的 node2vec 代码,并进行了一些初步的探索。这篇文章的目的是要理清楚两个问题:
- 到底什么是网络的同质性?什么是网络的结构性?
- DFS 是否擅长刻画同质性,BFS 是否擅长刻画结构性?为什么?
以下开始分析:
什么是网络的同质性?什么是网络的结构性?
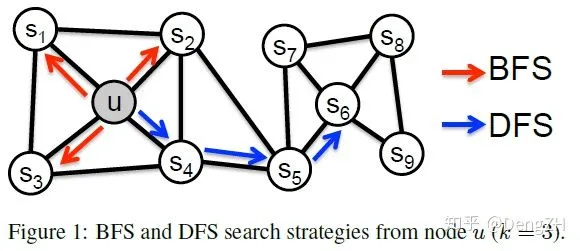
直觉上,我们认为同质性是指微观上,站在结点上来看,相邻的结点应该比较相似,那么 BFS 这种更强调 1 阶邻居的游走方式应该更能表达同质性(比如上图的结点 u 和相邻的 s1, s2, s3, s4);结构性是指宏观上,俯视整个网络,有着类似连接方式的结点应该比较相似,那么 DFS 这种能探索得更远得游走方式应该对学习结构性更有帮助(比如上图的结点 u 和结点 s6)。
但事实上,论文中给出的结论却是 DFS 擅长学习网络的同质性,BFS 擅长学习网络的结构性。从论文里的 Figure 3 中我们可以直观地进行观察:
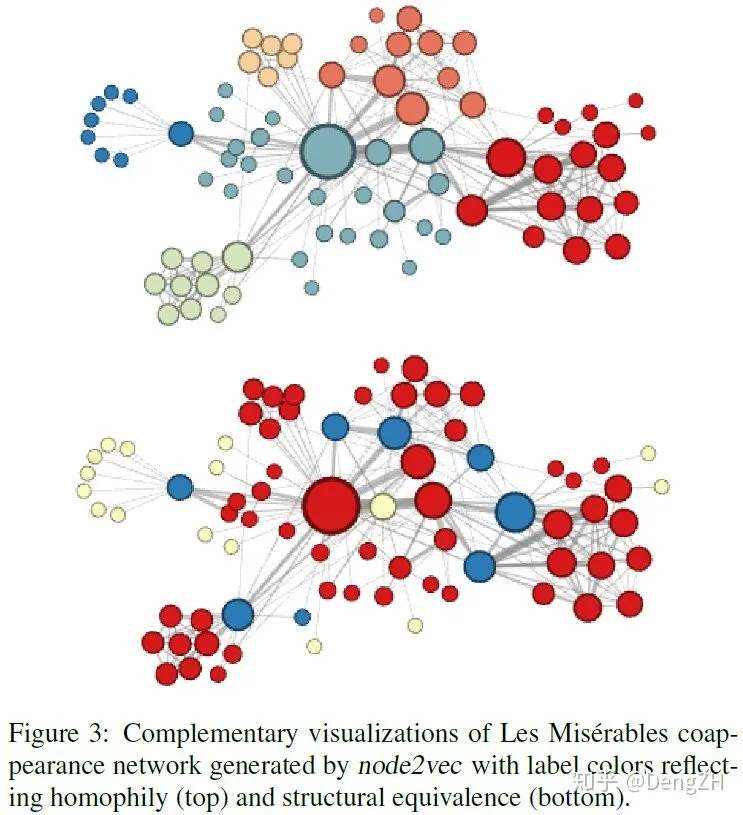
图的上半部分是倾向于 DFS(p=1,q=0.5)的,可以看到,这种方式得到的 embedding 似乎有很好的聚类性质,注意这里要看结点之间的连接而不是在 2D 平面上的距离,每个簇的边界结点跟内部的联系要比跟外部的联系更多一些。作者认为这反映了网络的同质性;
图的下半部分是倾向于 BFS(p=1,q=2.0),一个很明显的不同就是,这种方式得到的 embedding 似乎是按功能划分的,处于 graph 边缘的结点(黄色)有类似的 embedding,连接 graph 边缘和中心的结点(蓝色,在上半部分中作为簇边界的结点)有类似的 embedding,这些结点并不都是互相连接的,但是 node2vec 得到的 embedding 仍然能学习出这样的信息。作者认为这反映了网络的结构性。
通过这个图,我们再思考一下同质性和结构性的含义,就会发现和直觉上的含义不同了。同质性并不是一个微观上的性质,作者说的 同质性是能模型能找出每个簇的边界,使得簇内结点彼此联系的紧密程度要超过跟簇外结点的联系,这就要求模型有更大的感受野,DFS 这种能跳出局部的方式就很适合这个要求。
结构性就比较让人疑惑了,Figure 3 给出的关于结构性的表达似乎和我们直觉上差异不大,有着类似连接方式的结点会更相似。但是,BFS 竟然能做到这一点?那些 embedding 相似的结点甚至并不相互连接,BFS 为什么能有这种效果呢?
这里先给出后面做完实验后,感觉比较合适的一个解释。作者说的结构性并不是宏观上有相似的连接方式,而是指能够 充分学习微观上的局部结构。比方说结点处于一个三角形连接的内部(很多论文会称之为 motif),BFS 会加强对这个三角形的感知,而 DFS 则容易通过连向外界的边跳出去,所以 BFS 对局部结构得学习会比 DFS 好,这也符合对 Figure 3 的观察。但是,这并不能解释 Figure 3 中按功能划分结点这个现象,我的结论是:这种现象只能在合适的数据上,在合适的超参设定下被观察到。
DFS 是否擅长刻画同质性,BFS 是否擅长刻画结构性?为什么?
前面通过 Figure 3 来重新认识了同质性和结构性。但为什么 DFS 会擅长同质性,BFS 会擅长结构性呢?这就得再回顾一下 Figure 2,了解一下 DFS 和 BFS 到底做了什么:
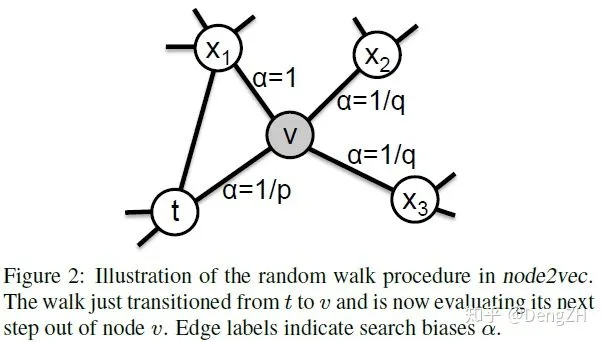
图中展示的是一次随机游走的中间过程,当前处于结点 v 上,上一步是从结点 t 到结点 v。
- x1 为结点 v 和结点 t 的共同邻居,设置边 v->x1 的权重为 1;
- t 为前序结点,设置边 v-> t 的权重为返回参数 p:
- p > 1 则下一步倾向于访问共同邻居;
- p < 1 则下一步倾向于回到前序结点。
- x2 和 x3 是结点 v 的其他一阶邻居结点,设置边的权重为进出参数 q:
- q > 1 则下一步倾向于访问共同邻居;
- q < 1 则下一步倾向于访问其他一阶邻居结点。
通过 p 和 q 这两个参数就可以调整游走的策略从而实现 DFS 或者 BFS。在 node2vec 中:
- DFS 是 p=1,q=0.5,
- 此时:P(访问其他一阶邻居结点) > P(返回前序结点)=P(访问共同邻居)
- BFS 是 p=1,q=2.0,
- 此时:P(访问其他一阶邻居结点) < P(返回前序结点)=P(访问共同邻居)
不妨在想象中检查一下,如果 P(访问其他一阶邻居结点) > P(返回前序结点)=P(访问共同邻居),那么随机游走就有可能一路推进不同的结点,构成一条重复结点较少的路径,确实符合 DFS 的理念。而如果 P(访问其他一阶邻居结点) < P(返回前序结点)=P(访问共同邻居),那么随机游走就有可能在一个较小的连接密集的局部中来会跳,构成一条重复结点较多的路径,这符合 BFS 的理念。
在得到随机游走的路径后,node2vec 就会把结点看作词,像 word2vec 学习词向量那样学习每个结点的 embedding 了。一般会采用 Skip-Gram 模式,也即使用中心词预测上下文,但无论是用 CBOW 还是 Skip-Gram,本质上都是假设一个词应该跟它所在句子的上下文词关系最密切(最相似),这也是我们理解 DFS 和 BFS 不同的关键。
如果随机游走侧重于 DFS,那么中心结点的上下文就可能同时包含不同阶的邻居;如果随机游走侧重于 BFS,那么中心结点的上下文就可能只包含有共同邻居的 1 阶邻居。因此,侧重于 DFS 的话,即使两个结点不彼此相连,只要它们有共同的 1 阶 2 阶邻居,也会得到相似的上下文,从而学到的 embedding 会比较像。这符合我们前面对同质性的分析,具备这种特质的 DFS 可以更好地找到簇的边界。
而侧重于 BFS 的话,处于同一个密集连接的局部的结点会更加相似,因为它们的上下文会有更多的重叠。这符合我们前面对结构性的分析,具备这种性质的 BFS 可以更好地感知结点所处的局部结构。
接下来,尝试用自己构造的网络来实验,看看结果是否会和上述分析一致。为了能观察到期望的结果,构造的网络必须:
- 有一定的聚簇现象;
- 包含密集连接的局部结构。
构造的网络比较小,embed 的维数可以直接设置为 2,这样可以直接 plot 在 2D 平面上直观地通过距离来衡量结点之间的相似度。随机游走序列的长度设置为 10。
首先,测试一下这个像 bridge 一样的网络:
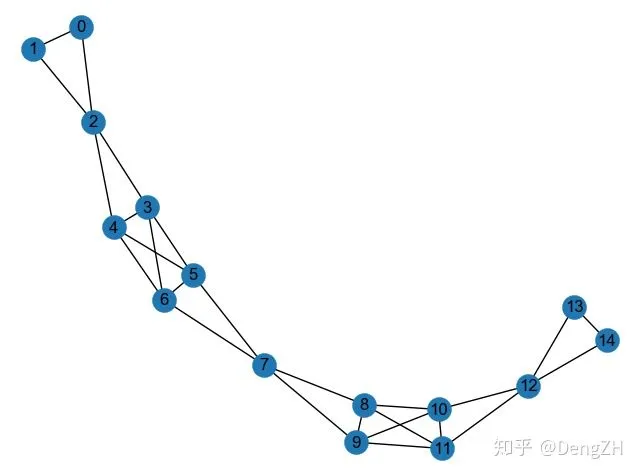
这个网络是对称的,有一个中心点 7,左右各有一个三角形局部结构和四边形的密集连接结构。将 node2vec 学到的结点 embedding 画出来:
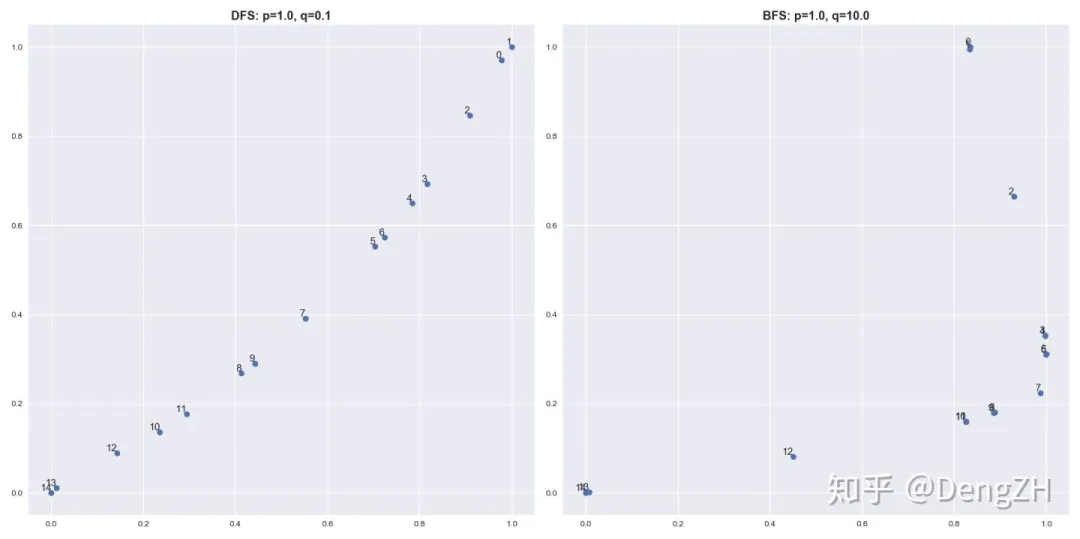
我们首先分析一下局部结构,可以看到 BFS 对局部结构非常敏感,同处一个局部结构内的结点的 embedding 几乎相同(比如结点 0 和 1),这与之前的分析一致。另外,我们也可以观察到,比起 DFS
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/%E4%BA%92%E8%81%94%E7%BD%91/%E8%AF%A6%E8%A7%A3%E5%9B%BE%E8%A1%A8%E7%A4%BA%E5%AD%A6%E4%B9%A0%E7%BB%8F%E5%85%B8%E7%AE%97%E6%B3%95/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


