语义向量召回之检索
作者: 蘑菇先生学习记
本篇文章主要介绍KDD 2020 Applied Data Science Track Papers中的一篇来自Facebook的语义检索文章,Embedding-based Retrieval in Facebook Search。关于样本、模型、训练等细节可以参考:负样本为王:评Facebook的向量化召回算法。本文重点关注其 工程实践 上的经验,也借此机会对基于PQ量化的近似近邻搜索 (ANN) 的原理做个梳理。
架构总览
首先从总体上预览一下paper提出的EBR系统的架构 (Embedding-based Retrieval System):
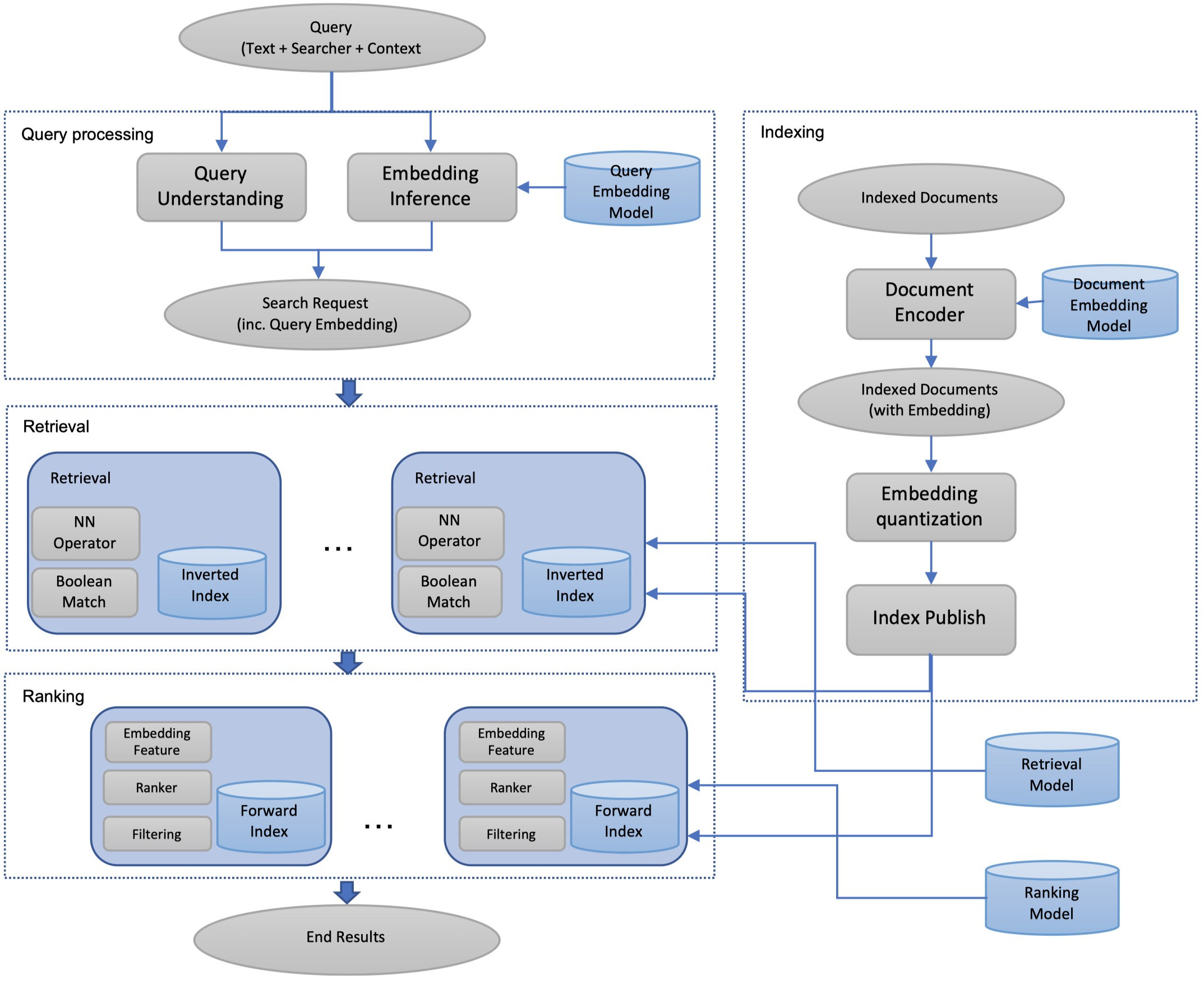
EBR系统架构图示意图
-
左上角是 查询处理模块,是双塔模型中的query-side embedding model
-
右上角 索引构建模块,是用document embedding model推断doc embedding后构造向量索引。
构造过程中,先拓展doc的metadata,加入doc embedding,并导入doc的正排索引中 (比如用于ranking的特征);
同时,通过向量量化技术来降低索引存储和计算距离代价,并将 量化的结果 存在倒排索引中。
这一部分也是paper中关注的重点,下文会重点介绍。
-
左侧中间部分是 检索模块,拿到query embedding后,可以通过精心为语义召回设计的 NN算子(Near Neighbor Operator) 计算距离并进行 语义召回。
召回的过程中,既支持原来的布尔匹配召回,也支持向量语义召回,还支持混合召回。
这部分下文也会重点介绍。
-
左下角是 排序模块,得到召回结果后,再经过排序模块进行实时排序,排序时会利用到 embedding特征。
paper中涉及工程实现细节的主要是 索引构建模块 和 检索模块。下文我会先介绍索引构建模块,这里头涉及很多向量量化的概念,比如PQ量化、粗糙量化、残差量化等,我会先介绍一些量化的背景知识,核心的索引过程和搜索过程,然后介绍在线检索模块,认识基于构建好的向量索引,线上是 如何运转 和 实现召回 的;接着探讨paper中提到的工程优化点和调参经验。最后,做个总结。
索引构建模块
基于Product Quantization的近似最近邻搜索,核心的一些问题预览一下:
- 问题描述,解决什么问题?
- 传统方法存在什么问题?
- 什么是向量量化?为什么要量化?量化场景下距离怎么计算?
- 什么是乘积量化?为什么要乘积量化?
- 什么是粗糙量化+残差量化?为什么要残差量化?
- 索引过程?搜索过程
问题描述
给定D维向量和集合 ,需要找到与距离最短的 k 个最近邻。距离的衡量可以是欧式距离、余弦距离等。
暴力搜索问题
如果以最粗暴的方法进行穷举搜索,构造 距离矩阵 的复杂度为O(D N^2):。从距离矩阵中查找到 k个最近邻,最小堆,则复杂度为O((N-k)\log k)。
举个例子:假设N=2000W, k=1000,则构造的距离矩阵包含 400T 个元素,假设每个距离值32bit,至少占用1600TB空间,构建距离矩阵的时间是 10^{17} 量级,查找Top-K搜索时间是 10^{9} 量级。
向量量化
所谓向量量化,就是将原来无限的空间R^D映射到一个有限的 向量集合\mathcal{C} = \{\boldsymbol{c}_i, i\in[1,l]\}中,其中||\mathcal{C}||=l是一个自然数。将这个从 R^D 到集合的函数\mathcal{C}记为q,则\forall q(y) \in \mathcal{C},在信息论中称\mathcal{C}为codebook。即:通过q(y)来 近似 代表y。
聚类量化
最常用的就是k-means聚类,通过聚类后的 聚类中心向量 来近似 量化 原始的向量。 聚类中心的个数 即为 codebook大小。因为量化的存在, 任意两个向量之间的距离 可以通过对应的 量化向量的距离 进行近似,也就是聚类中心向量的距离。因为聚类中心的个数 小了 很多,故计算距离的复杂度也下降了很多。(显然,这种方式太粗糙了,误差很大。除非聚类数非常大,极端情况下,聚类数等于样本数时,每个样本一个聚类簇,此时无误差,但是没有起到减少计算复杂度的目的)
聚类量化的结果:产出聚类中心向量的过程对应train的过程的一部分。量化后,每个向量都可以用聚类簇中心下标ID 来 标识,根据ID可以获取聚类簇的中心向量。
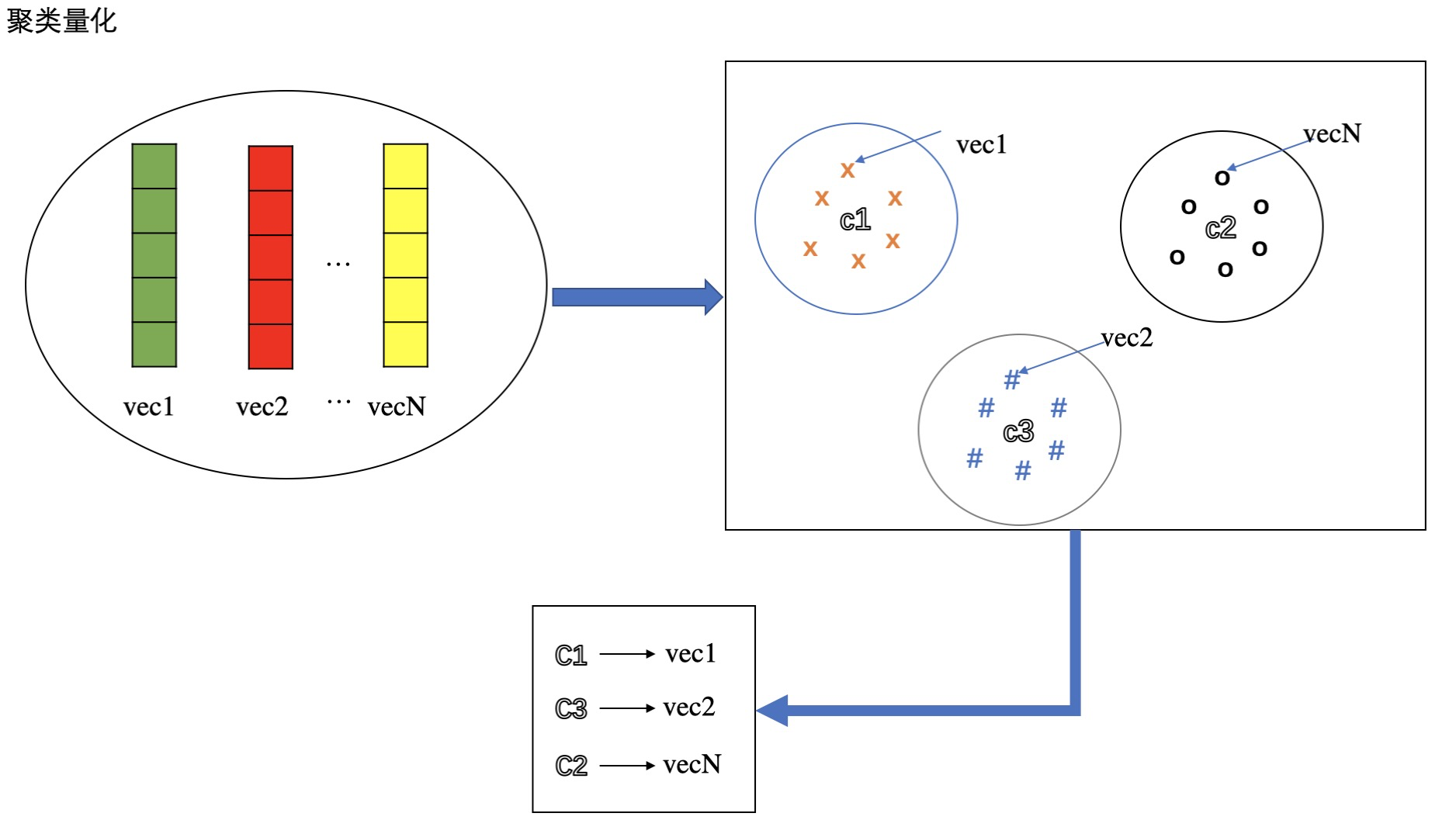
聚类量化过程示意图如上图所示,N个向量,通过聚类量化产生多个聚类中心,每个向量属于某个聚类簇中,那么就用该聚类簇对应的中心向量来量化该向量,可以用聚类簇中心对应的下标ID来表示,比如:C1量化vec1。
Faiss中对应的实现是 IndexIVFFlat。
乘积量化
动机:即:PQ量化,很多时候我们向量不同部分之间的分布不同 的,比如下图(3段向量),因此可以考虑对 向量分段,并分别进行 分块量化。这个只是直觉原因,本质原因下文讲。

乘积量化定义:将向量分成m个不同的部分,对每个部分进行向量量化,假设平均划分,则每个部分的维度大小为:D^{\star}=D/m;一个向量,可以划分为m组向量,第i组向量形如:[x_{i\_1},x_{i\_2},…,x_{i\_D^{\star}}],每组的codebook为C_i,对应的量化器记为q_i, (\forall q_i(x_{i^{\star}}) \in \mathcal{C_i})。则最终的全局codebook就是\mathcal{C} = \mathcal{C_1} * \mathcal{C_2} … * \mathcal{C_m} ,乘积量化的名称也来源于此。
分块量化也可以采取聚类量化来实现,则 分块聚类中心的个数 即为 分块codebook 的大小。相当于在这个方法下,对每个向量,有【 m个分块向量】来量化它,即:【m个分块聚类中心向量】。 示意图如下:
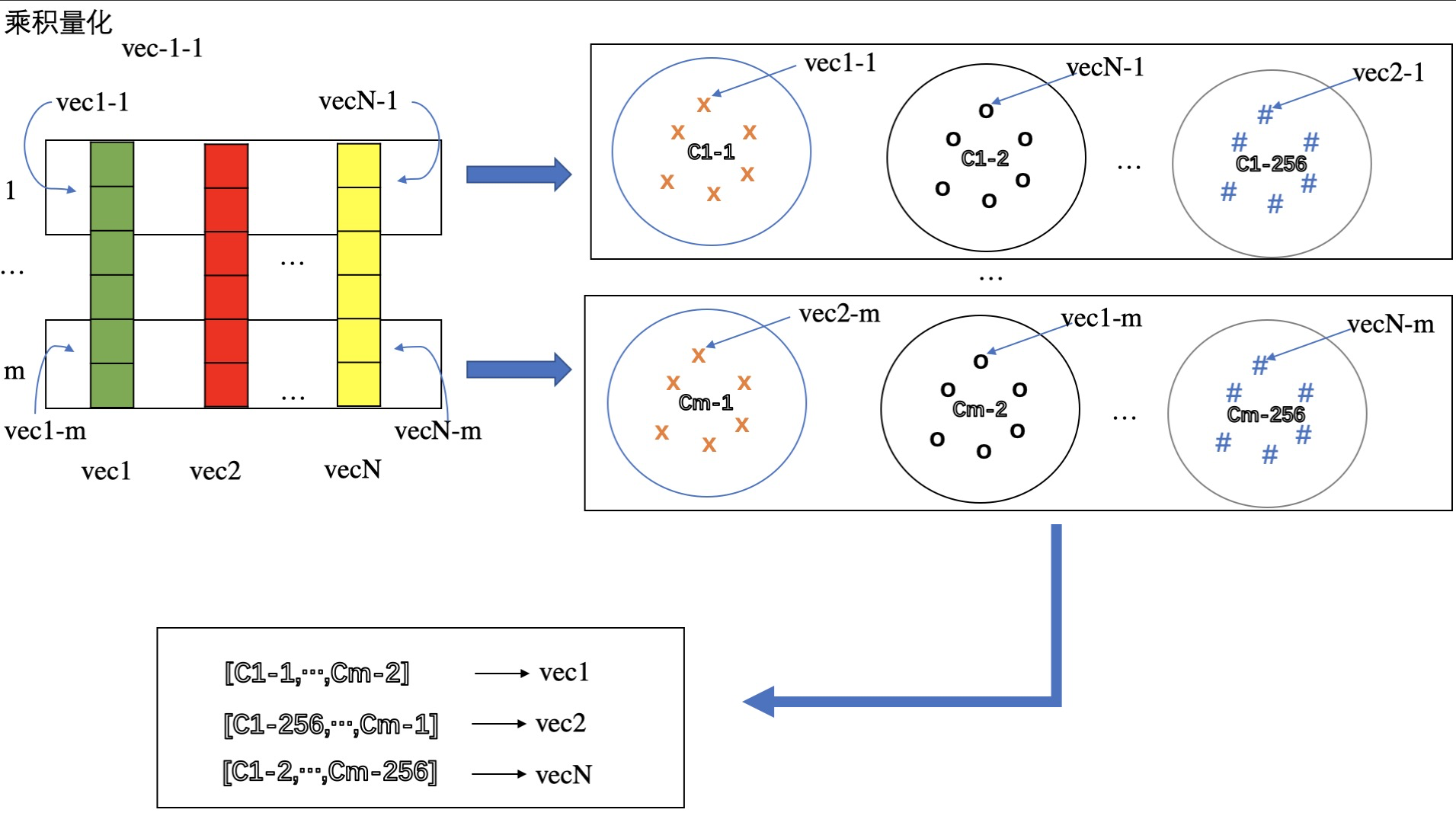
PQ量化过程示意图
如上图所示,将原始向量等分为m组分块向量,每组都进行聚类量化,那么每个向量就有m个分块聚类中心向量来表示,比如vec1用C_{1-1}, …,C_{m-2}, …, 共m个向量来量化。
乘积量化的好处:假设每个子codebook大小一样,记做||\mathcal{C}_i||=k^{\star},排列组合一下,那么相当于能表达的向量空间容量是这么大,||k^{\star}||^m,但是只需要m k^{\star}的codebook空间,这也是乘积量化大幅度降低空间占用的本质原因。PQ量化原论文中给出的经验取值是:k^{\star}=256,m=8,即:分成8块,每个分块的codebook大小为256,对应的向量空间大小为约$256^8=2^{64}≈1.8 \times 10^{19}$,能够表达的向量个数足够大了。
乘积量化结果:m \times k^{\star}个分块聚类中心向量。每个向量可以用m个分块聚类簇中心下标 ID来标识,所有ID连起来称为 code。假设每块的聚类中心个数为256,则需要8bits,即1byte标识某分块下哪个聚类中心,m块则需要m bytes,即code大小为m bytes。
粗糙量化+残差量化
核心思想:层次化量化,这个也是Faiss中PQ索引的实现方式。其中粗糙量化使用聚类量化,用划分到的 粗糙聚类簇的中心向量 来 粗粒度 量化该向量,该结果存在较大的误差;接着对残差结果进行 细粒度 乘积量化。这样的话,误差就小了。
1. 总体上,每个向量先进行粗糙量化划分到某个粗糙聚类簇里,1个向量对应1个粗糙聚类簇标识,通常称为粗糙量化ID;
2. 然后计算残差向量,即:向量-聚类簇中心向量,再对该残差向量进行分块,并进行细粒度分块残差量化。残差量化的时候,每一块对应一个细粒度聚类簇,1个向量M块,则对应M个细粒度聚类簇标识,通常称为残差量化code。
3. 为什么用残差量化?原始向量可能会有特别大的分布差异/不平衡,也就是说可能聚类后,不同聚类簇分布得非常分散,每个簇所拥有的样本数极度不平衡。但是通过残差化后,即:每个样本向量减去所属的聚类簇中心向量后,残差向量之间的差异就不太大了,然后再对残差向量进行量化,就能更精确的近似原向量。
过程:具体而言,向量库先构造一个小规模codebook \mathcal{C}_c,量化器为qcqc。这个就是所谓的粗糙量化,或者称为粗糙聚类。接着,每个向量y都会有一个残差r(y)=y−q_c(y)。具体而言:记残差量化步骤的量化器为q_p,则 y 可以通过q_c(y)+q_p(y−q_c(y))来表示。
y = q_c(y) + q_p(y-q_c(y)) = y_C + y_R
其中,y_C是粗糙量化结果,y_R是残差量化结果。
这样的话,【 查询向量x】和y之间的距离:
d(x,y) = ||x-y||^2=||x-y_C-y_R||^2=\underbrace{||x-y_C||^2}_{\text{term 1}} + \underbrace{||y_R||^2 + 2 y_C y_R}_{\text{term 2}} - \underbrace{2 x y_R}_{\text{term 3}}
-
term 2 与查询向量x 无关, 可以提前计算好;
-
term 1 求x和y的粗糙量化向量的欧式距离,最多计算O(k)次,k为粗糙聚类中心个数。
-
term 3 求x和y的残差量化向量的内积,遍历所有簇的时候,最多计算O(mk^{\star}) 次,mk^{\star}为分块聚类中心向量。
对应Faiss中的实现是 IndexIVFPQ。
做个小结,量化的结果:
聚类量化乘积量化粗糙量化+残差量化k个聚类簇中心下标id****m x k 个分块聚类中心下标组成的 code*k个聚类簇中心下标ID,m x k 个分块聚类中心下标组成的 code*
也就是说,为了表示每个doc的 量化结果,可以为doc可以添加两种 结构化字段: 粗糙量化id, 残差量化code,用于实时检索使用。
倒排索引
索引结构
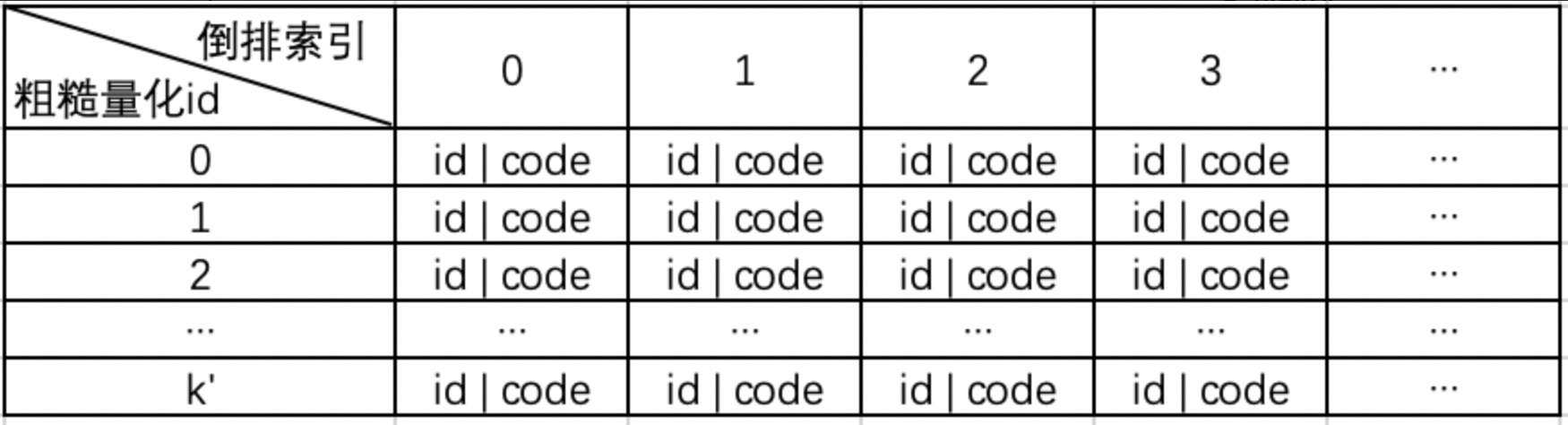
建立从粗粒度聚类中心id 到 doc的映射关系,其中doc的信息包括:向量id, 向量的残差量化code。每个doc通过粗糙聚类中心id和残差量化code就能知道原始向量如何映射到量化向量。
整个倒排索引不需要存储原始向量本身,索引结构存储的内容:
-
存储标识: 粗糙量化id, doc id 和残差量化 code。
空间占用很小。m bytes 残差量化code,即:code_size或者pq_bytes。这个数越大,那么细粒度聚类簇越大,则精度越高。
基于id,可以找到对应的粗粒度量化向量 (共k个) ; 基于code 可以找到对应 细粒度残差量化向量(共 m x k\* 个)。
索引构建过程
搜索场景中,y可以理解为doc。
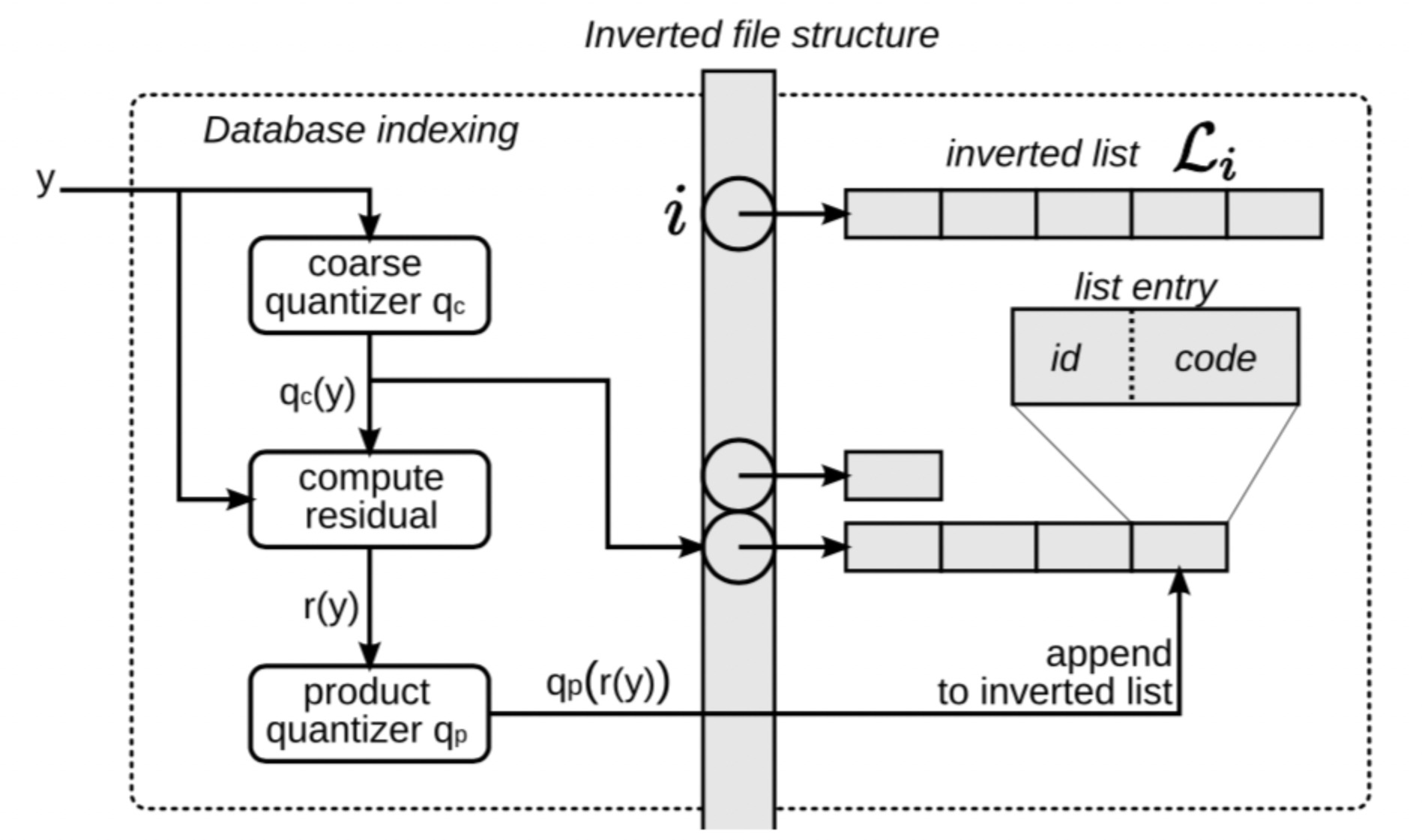
- 通过粗糙量化器 q_c将向量 yy 映射到q_c(y),即粗糙量化。这样就知道挂到哪个链表上了。
- 计算残差r(y) = y-q_c(y)
- 将残差 r(y)量化到 q_p(r(y)),其中包含了 m 个分组,每个分组有对应的一个细粒度聚类簇ID,用1byte表示,则共m bytes,对应code标识。
- 构造一个 id|code entry,其中id是doc的标识,code是残差量化标识。
搜索过程
搜索场景中,x可以理解为查询向量。
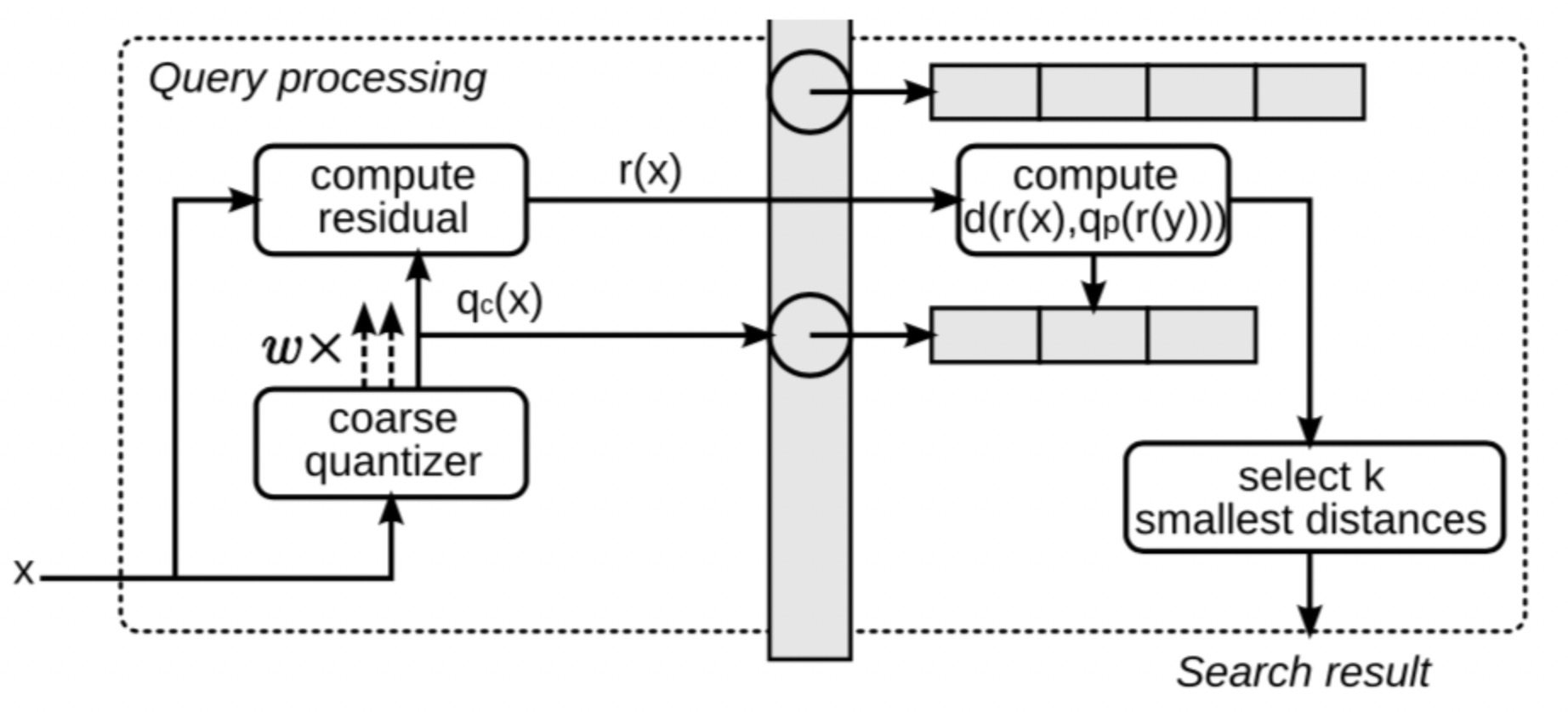
- 通过粗糙量化器来量化 查询向量x,即:找到离x最近的w个粗糙聚类簇。实际上是用于 限定搜索的范围,只搜索w个粗糙聚类簇ID索引下的向量。w是个超参数,即nprobes,量化的结果 对应term 1。
- 选定某个粗糙聚类簇,
-
计算 x 和该粗糙聚类簇下的 k*(默认即256)个中心点向量的内积。对应term 3,计算时间复杂度 O(m x D/m x k*) = O(Dk*),记录下来,下一步查表用。
-
遍历该聚类簇下的doc文档, 计算距离时,实际上全是 查表操作,term 2是提前算的,term 1粗糙量化时算的,term 3上一步算的。查表时间复杂度实际上是 O(m)
w个粗糙聚类簇,搜索时间复杂度为 O(w(Dk* + m)), 另外,返回top-k的话,要加上最小堆排序时间。
-
检索模块
布尔检索
Facebook在自研的检索引擎 Unicorn 中支持了第一代的近邻搜索。
首先简单介绍下Unicorn。Unicorn原本的检索方式主要以Term布尔匹配为主。
- doc侧:以Term词袋的方式来表示doc,会基于Term的语义来区分命名空间。Term上还可以添加一些term特定的 payload 信息。举例:John living in Seattle会表示成【 text: john and location: seattle】。
- query侧:定义 Term-level 的布尔表达式来表示query。举例:下述query主要返回doc的文本中有john和smithe字眼,并住在seattle和menlo_park的用户。

向量检索
为了支持embedding,需要扩展 doc和query的表示
- doc侧:添加结构化字段 key 来拓展doc词袋表示,形如:**,**比如:key=model-141795009,代表了产出doc embedding model的版本。设置该字段方便部署多种embedding版本。
- query侧:添加 nn算子,即: nn : radius ,使用时,通过计算query embedding和模型产出的doc embedding的距离,来匹配距离在指定radius内的文档。radius此处起到 阈值约束 的作用。
索引和计算向量距离时,Facebook将 向量索引和向量在线检索 通过某种方式转化成上述已有的 布尔检索语言,很巧妙,可以完美融入现有的**布尔检索系统,**而不需要重新写一套系统。
先做个对应关系。
布尔匹配检索语义向量检索Term粗糙聚类中心ID 标识,Cluster-IDPayload细粒度聚类中心CODE 标识, Cluster-Code
doc侧:每个doc embedding会被 量化 并转成一个 term 和一个 payload,相当于是两个doc的结构化字段,完美兼容已有的检索系统Unicorn的设计。
- term,其实就是用于标识倒排索引中,该doc属于哪个 粗粒度聚类簇 (用于粗糙聚类量化)
- payload,用于标识每个分块向量下的 细粒度聚类簇(用于残差量化)
query侧:
-
term: (nn) 重写成和粗糙聚类相关的 term。
重写规则:计算query embedding和所有粗糙聚类中心距离,选出nprobes个最近的,用粗糙聚类中心ID来标识 (和doc的结构化字段 Cluster-ID 进行比较),不同聚类中心对应的Term之间的关系就是or的关系。
-
payload: 对query进行残差量化,得到满足 radius约束条件 的细粒度聚类中心,用code标识**。**
重写规则:对每个粗糙聚类簇,计算query embedding和其细粒度聚类中心的距离,距离 满足<radius约束 的细粒度聚类中心对应的Code 取值记录一下 (和doc的 结构化字段Cluster-Code 进行比较),Code之间是OR关系,但是Code和ID是AND关系。
举个query改写的例子:
or ((and( (term(Cluster-ID, '粗糙聚类中心ID-a')),
(or (term(Cluster-Code, '残差聚类中心ID-a1'), term(Cluster-Code, '残差聚类中心ID-a3'),...)))
),
(and( (term(Cluster-ID, '粗糙聚类中心ID-b')),
(or (term(Cluster-Code, '残差聚类中心ID-b1'), term(Cluster-Code, '残差聚类中心ID-b4'),...)))
),
...
)
另外,作者强调了radius-mode和topk-mode的差异,radius方式的性能和质量更高。radius是一种 受限制 NN搜索。top-K需要扫描整个�
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/%E4%BA%92%E8%81%94%E7%BD%91/%E8%AF%AD%E4%B9%89%E5%90%91%E9%87%8F%E5%8F%AC%E5%9B%9E%E4%B9%8B%E6%A3%80%E7%B4%A2/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


