心率呼吸率分离算法
基于毫米波雷达或者可穿戴心冲击检测设备,采集人的体征信号,心冲击信号,脉搏压力信号,根据得到的压力信号,进行下列步骤的算法分析:
一、心冲击信号数据分析
得到的信号如图1:
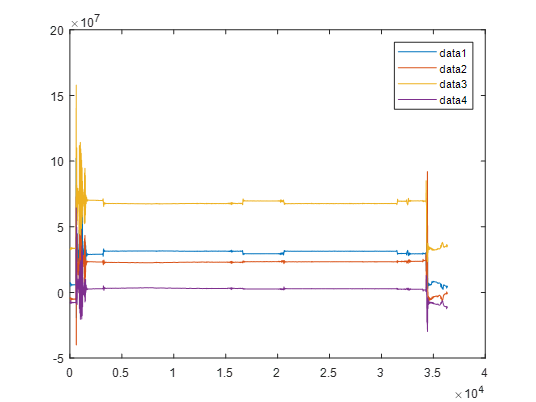 选取其中(0.2-3.4)×104这一段(即去除了首尾上下床的信号,只保留了中间平躺状态下的信号)来进行分析,选取其中一路信号(data4)进行分析,其波形如图2:
设该信号为X(n),则可得到如下式子:
x(n)=r(n)+h(n)+ε(n)
其中r(n)为呼吸信号,h(n)为心跳信号,ε(n)为其他噪声信号。
选取其中(0.2-3.4)×104这一段(即去除了首尾上下床的信号,只保留了中间平躺状态下的信号)来进行分析,选取其中一路信号(data4)进行分析,其波形如图2:
设该信号为X(n),则可得到如下式子:
x(n)=r(n)+h(n)+ε(n)
其中r(n)为呼吸信号,h(n)为心跳信号,ε(n)为其他噪声信号。
二、心跳信号处理
根据百科资料,安静状态下,成人正常心率为60~100次/分钟,理想心率应为55~70次/分钟,因此心跳信号的频率应该是在0.9-1.7Hz左右,呼吸信号的频率较低,成年人为大概16~20/分钟,频率低于0.5Hz,所以可以用一个带通滤波器滤去呼吸信号以及高频的噪声信号,选择滤波器为巴特沃斯滤波器,它的平方幅度函数定义为:
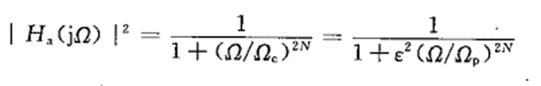 式中,N是滤波器的阶数,Ω_c称为3dB截止频率,ε是控制通带波纹幅度的参数。选定频带为0.7Hz~2Hz,可以得到滤波后的信号如图3:
式中,N是滤波器的阶数,Ω_c称为3dB截止频率,ε是控制通带波纹幅度的参数。选定频带为0.7Hz~2Hz,可以得到滤波后的信号如图3:
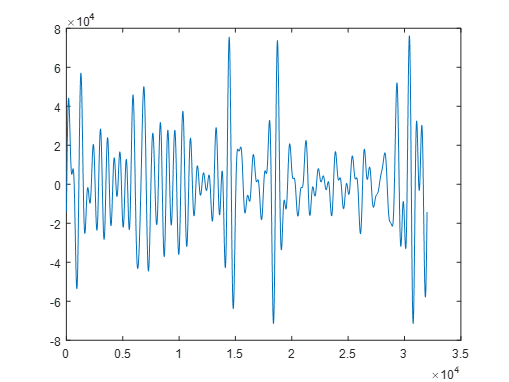 图3 经过带通滤波器后的data4信号
针对该信号进行HHT(希尔伯特-黄变换),不同于傅里叶变换只能处理线性非平稳信号,这个变换可以分析非线性非平稳信号。并且傅立叶变换、短时傅立叶变换、小波变换都受Heisenberg测不准原理制约,即时间窗口与频率窗口的乘积为一个常数。这就意味着如果要提高时间精度就得牺牲频率精度,反之亦然,故不能在时间和频率同时达到很高的精度,这就给信号分析处理带来一定的不便。而HHT不受Heisenberg测不准原理制约,它可以在时间和频率同时达到很高的精度,这使它非常适用于分析突变信号。
该方法分为两步,第一步是先进行EMD(经验模态分解),这个过程依据信号特点自适应地把任意一个复杂信号分解为一系列本征模态函数(IMF)。它满足如下两个条件:
(1) 信号极值点的数量与零点数相等或相差是一;
(2) 信号的由极大值定义的上包络和由极小值定义的下包络的局部均值为零。
最终的信号可以表示为如下式子:
图3 经过带通滤波器后的data4信号
针对该信号进行HHT(希尔伯特-黄变换),不同于傅里叶变换只能处理线性非平稳信号,这个变换可以分析非线性非平稳信号。并且傅立叶变换、短时傅立叶变换、小波变换都受Heisenberg测不准原理制约,即时间窗口与频率窗口的乘积为一个常数。这就意味着如果要提高时间精度就得牺牲频率精度,反之亦然,故不能在时间和频率同时达到很高的精度,这就给信号分析处理带来一定的不便。而HHT不受Heisenberg测不准原理制约,它可以在时间和频率同时达到很高的精度,这使它非常适用于分析突变信号。
该方法分为两步,第一步是先进行EMD(经验模态分解),这个过程依据信号特点自适应地把任意一个复杂信号分解为一系列本征模态函数(IMF)。它满足如下两个条件:
(1) 信号极值点的数量与零点数相等或相差是一;
(2) 信号的由极大值定义的上包络和由极小值定义的下包络的局部均值为零。
最终的信号可以表示为如下式子:
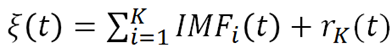 传统的傅里叶分析用一系列三角基函数对信号进行正交运算,但是对于非平稳信号,比如频率一直变化的信号,得到的傅里叶谱只是某一段时间内频率的均值,无法准确描述频率-时间的变化。瞬时频率的定义方法不唯一,但使用Hilbert变换来定义瞬时频率能够生成复解析信号,进而得到复平面上具有明确解析意义的瞬时频率。对于实信号x(t),其复解析信号为
传统的傅里叶分析用一系列三角基函数对信号进行正交运算,但是对于非平稳信号,比如频率一直变化的信号,得到的傅里叶谱只是某一段时间内频率的均值,无法准确描述频率-时间的变化。瞬时频率的定义方法不唯一,但使用Hilbert变换来定义瞬时频率能够生成复解析信号,进而得到复平面上具有明确解析意义的瞬时频率。对于实信号x(t),其复解析信号为
 实部虚部的幅角对时间求导即得到瞬时频率。
实部虚部的幅角对时间求导即得到瞬时频率。
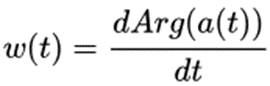 对每个IMF进行Hilbert变换,原信号x(t)可以表示如下,即Hilbert谱
对每个IMF进行Hilbert变换,原信号x(t)可以表示如下,即Hilbert谱
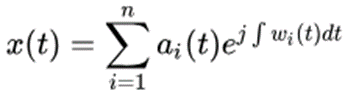 在经过经验模态分解后,得到7个IMF,如图4
在经过经验模态分解后,得到7个IMF,如图4
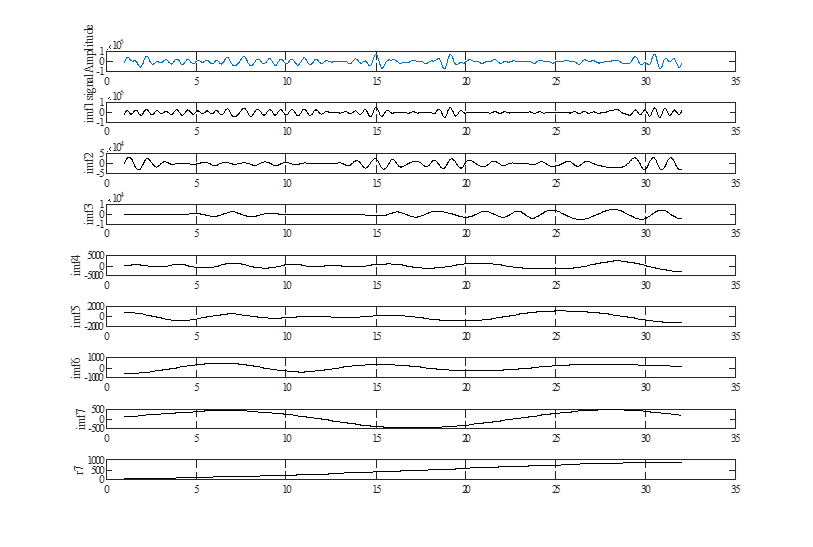 图4 经过经验模态分解后的信号波形
下一步应当是进行HT变换,然后计算瞬时频率,这里尚未弄好代码,目前还无法得到,还在调试中。因此暂时先用傅里叶变换得到全局的频率,得到频谱图如图5,由频谱图可以确定能量最大对应的频率为0.9375Hz,所给的数据中说明实验者的心跳频率大约在1Hz。同理选择data1时测得频率为0.9375Hz,选择data2时测得频率为1.063Hz,选择data3时测得频率为0.875Hz,令data5=data2+data3-data1-data4,此时得到频率为0.9375Hz。
图4 经过经验模态分解后的信号波形
下一步应当是进行HT变换,然后计算瞬时频率,这里尚未弄好代码,目前还无法得到,还在调试中。因此暂时先用傅里叶变换得到全局的频率,得到频谱图如图5,由频谱图可以确定能量最大对应的频率为0.9375Hz,所给的数据中说明实验者的心跳频率大约在1Hz。同理选择data1时测得频率为0.9375Hz,选择data2时测得频率为1.063Hz,选择data3时测得频率为0.875Hz,令data5=data2+data3-data1-data4,此时得到频率为0.9375Hz。
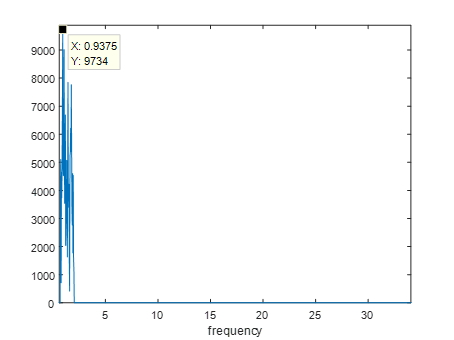 图5 信号频谱图
三、呼吸信号处理
根据资料,成年人的呼吸频率为12-20次/分。
1.低通
设定低通频率为0.4Hz,选用巴特沃斯滤波器,设定阶数为3,选取其中一路信号,得到滤波后的波形如下图:
图5 信号频谱图
三、呼吸信号处理
根据资料,成年人的呼吸频率为12-20次/分。
1.低通
设定低通频率为0.4Hz,选用巴特沃斯滤波器,设定阶数为3,选取其中一路信号,得到滤波后的波形如下图:
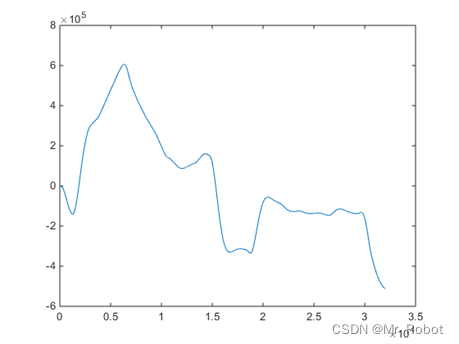 图 6 滤波后的信号波形
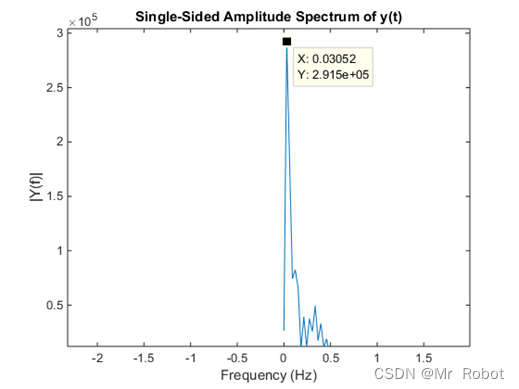
然后进行fft变换得到频谱图如下,表明其中并没有周期信号,选择其他路信号以及综合几路信号均未检测到。
图 6 滤波后的信号波形
然后进行fft变换得到频谱图如下,表明其中并没有周期信号,选择其他路信号以及综合几路信号均未检测到。
 2.带通
设定带通频率为0.15-0.3Hz(邮件中说明该人呼吸频率为10次/分,大约为0.17Hz),选用巴特沃斯滤波器,设定阶数为2,选取其中一路信号,得到滤波后的波形如下图:
2.带通
设定带通频率为0.15-0.3Hz(邮件中说明该人呼吸频率为10次/分,大约为0.17Hz),选用巴特沃斯滤波器,设定阶数为2,选取其中一路信号,得到滤波后的波形如下图:
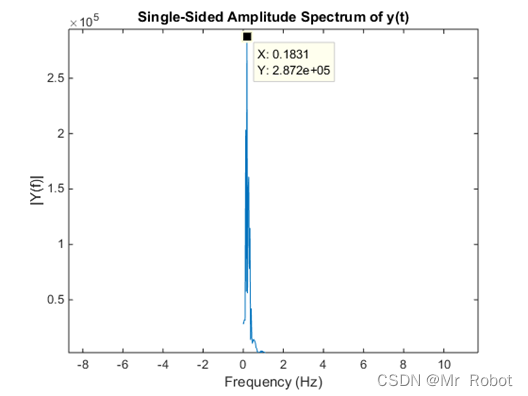
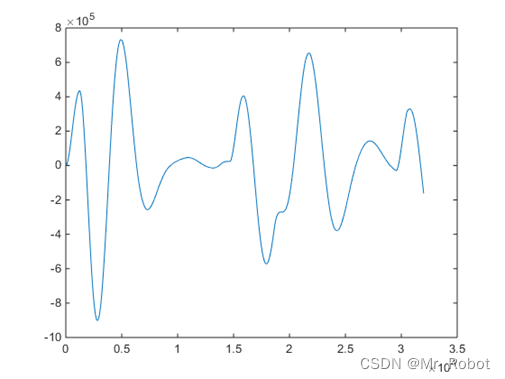 图 8 滤波后的信号波形
图 8 滤波后的信号波形
 附:前人文献中查到的呼吸心跳波形
附:前人文献中查到的呼吸心跳波形
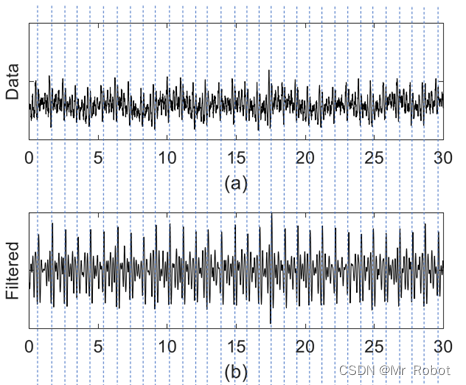 图10 正常心跳波形
图10 正常心跳波形
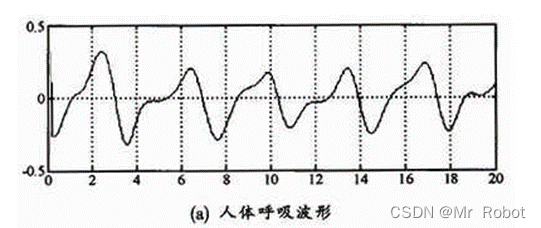 图11 连续波雷达监测到的呼吸波形
图11 连续波雷达监测到的呼吸波形
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/ecg/004-%E5%BF%83%E7%8E%87%E5%91%BC%E5%90%B8%E7%8E%87%E5%88%86%E7%A6%BB%E7%AE%97%E6%B3%95/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


