单隐藏层就已经需要14GB的参数了!平移不变性:识别器不会因为像素的位置而发生改变局部性:找Waldo只需要看局部的信息即可,不需要看全局的信息个人理解:由前面的例子可知,全连接层需要的参数量会非常多,这也就使得MLP受到了限制。但是为了解决问题,提出了“平移不变性”和“局部性”两个性质。我们从全连接层出发,应用两种性质,对原本的计算方式做一些改进,也就得到了卷积层的计算方式。相较于全连接,平移不变性使得卷积的权重在一定范围内,v是相同的;但是由于局…

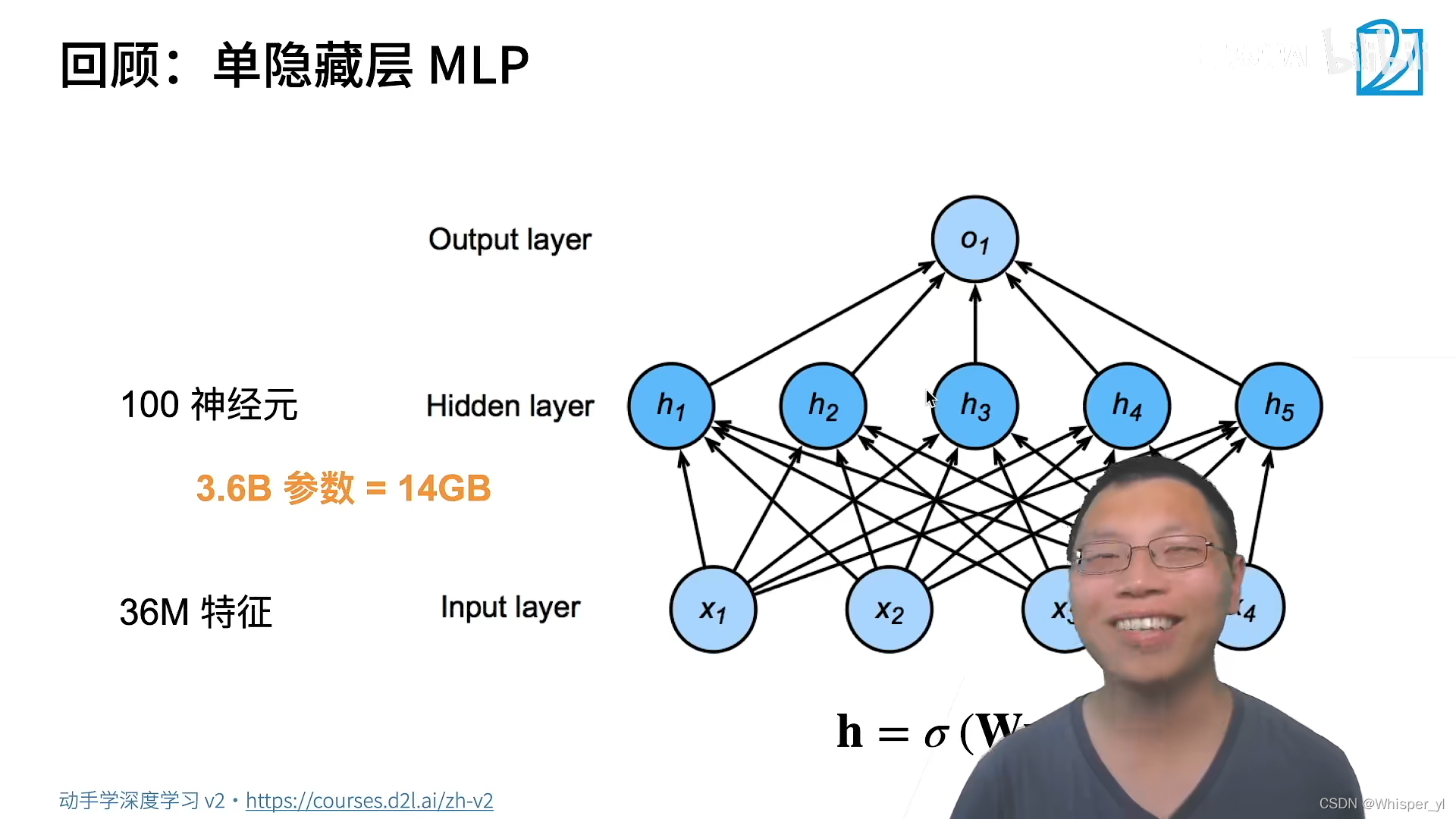
单隐藏层就已经需要 14GB 的参数了!
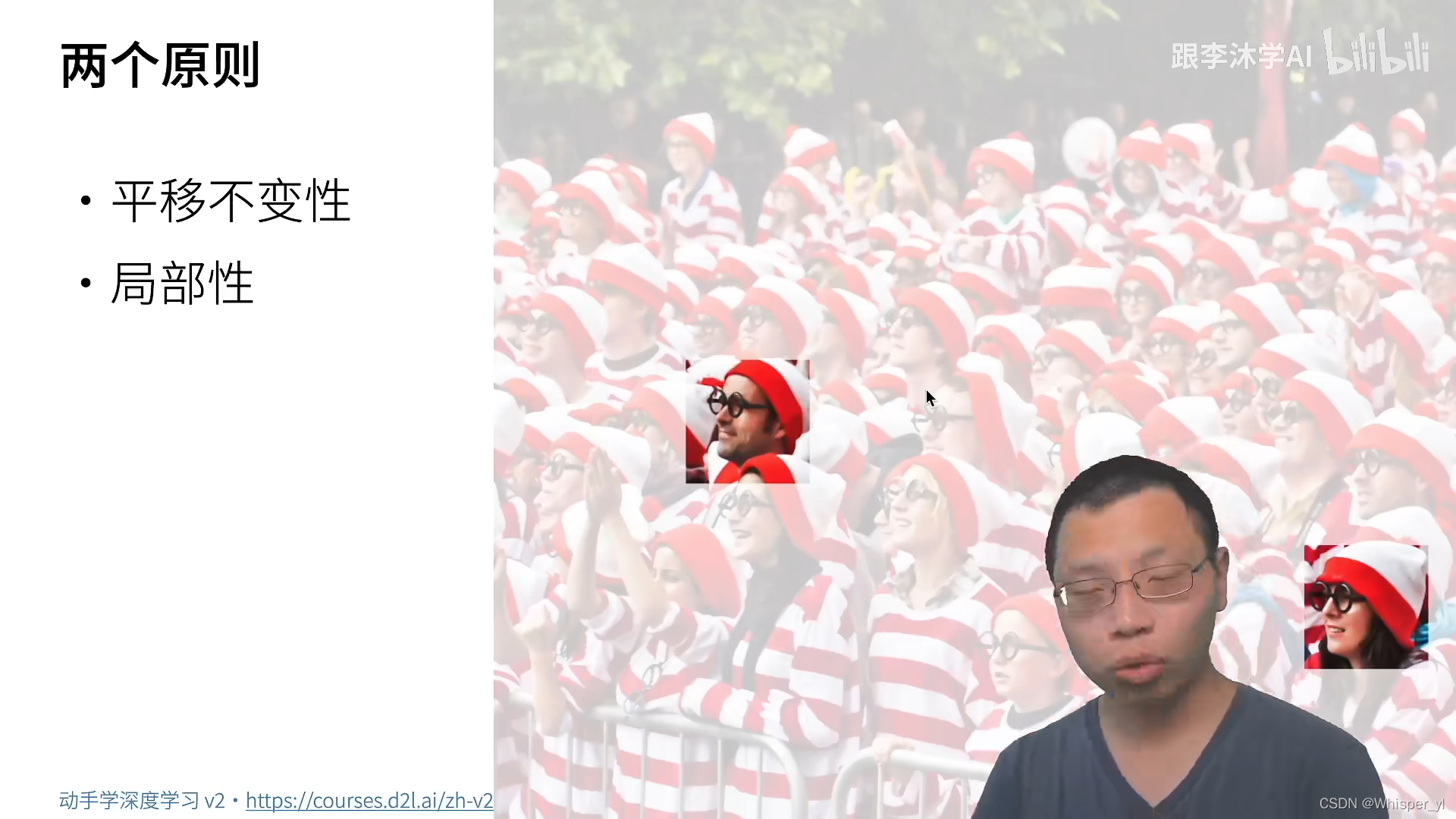
平移不变性:识别器不会因为像素的位置而发生改变
局部性:找 Waldo 只需要看局部的信息即可,不需要看全局的信息




个人理解:由前面的例子可知,全连接层需要的参数量会非常多,这也就使得 MLP 受到了限制。但是为了解决问题,提出了 “平移不变性” 和“局部性”两个性质。我们从全连接层出发,应用两种性质,对原本的计算方式做一些改进,也就得到了卷积层的计算方式。相较于全连接,平移不变性使得卷积的权重在一定范围内,v 是相同的;但是由于局部性的存在,当 | a|,|b| > Δ的时候,v = 0。这样就极大地优化了参数量。由此,卷积层是一个特殊的全连接层,那么卷积层自然也像全连接层一样,能够进行梯度计算和反向传播从而学习到参数。





import torch
from torch import nn
from d2l import torch as d2l
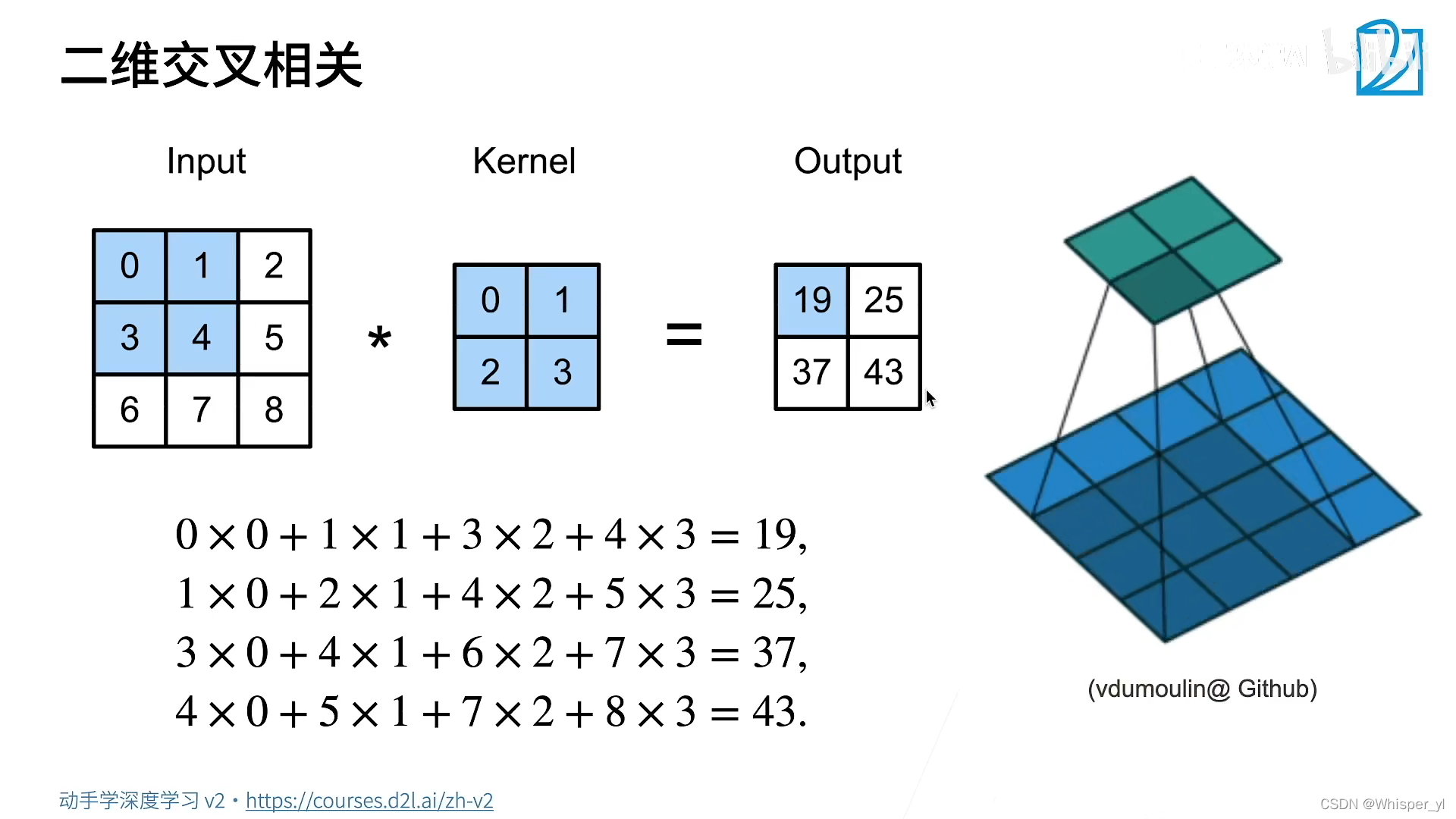
def corr2d(X, K):
"""计算二维互相关运算"""
h, w = K.shape
Y = torch.zeros((X.shape[0] - h + 1, X.shape[1] - w + 1))
for i in range(Y.shape[0]):
for j in range(Y.shape[1]):
Y[i, j] = (X[i: i + h, j: j + w] * K).sum()
return Y
X = torch.tensor([[0.0, 1.0, 2.0], [3.0, 4.0, 5.0], [6.0, 7.0, 8.0]])
K = torch.tensor([[0.0, 1.0], [2.0, 3.0]])
print(corr2d(X, K))
# 实现二维卷积层
class Conv2D(nn.Module):
def __init__(self, kernel_size):
super().__init__()
self.weight = nn.Parameter(torch.rand(kernel_size))
self.bias = nn.Parameter(torch.zeros(1))
def forward(self, x):
return corr2d(x, self.weight) + self.bias
# 简单应用:检测图像中不同颜色的边缘
X = torch.ones((6, 8))
X[:, 2: 6] = 0
print(X)
K = torch.tensor([[1.0, -1.0]])
Y = corr2d(X, K)
print(Y)
# 学习由X生成Y的卷积核
conv2d = nn.Conv2d(1, 1, kernel_size=(1, 2), bias=False)
# 两个1分别表示批量大小数和通道数
X = X.reshape((1, 1, 6, 8))
Y = Y.reshape((1, 1, 6, 7))
for i in range(10):
Y_hat = conv2d(X)
l = (Y_hat - Y) ** 2
conv2d.zero_grad() # 梯度设置为0
l.sum().backward()
conv2d.weight.data[:] -= 3e-2 * conv2d.weight.grad # 学习率:3e-2
if (i + 1) % 2 == 0:
print(f'batch {i + 1}, loss {l.sum():.3f}')
print(conv2d.weight.data.reshape((1, 2)))
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/tlg/output/%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0%E7%AC%94%E8%AE%B0-%E5%8D%B7%E7%A7%AF%E5%B1%82/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


