原文： 姚凯飞

「无法衡量就无法优化」，对于互联网产品而言，不仅是推荐系统，整个app系统的更新迭代必然需要建立一套 「度量衡」，来 「把控整个流程优化的方向」 。而abtest系统就是一个很好的进行变量控制和优化方向选取的 「工具」， 「循环:衡量-发现-迭代-验证」 。所谓 「精细化迭代」 是一种建立在数据基础上的思维方式—— 「用较少的成本获得较好的效果」。 「无数据，不优化」， 线上分流实验是进行推荐算法优化的必由之路。并且abtest不仅是推荐迭代的利器，他还可服务于所有需要逐步完善的产品迭代。有人说为什么需要abtest，为什么不能够前后进行实验比较；因为同时期测试的abtest非常有必要的原因是不同时间的测试无法说明b比a好，通常 「时间也是一个变量」，比如电商的双十一等。

在网络分析中，A / B测试（桶测试或分流测试）是一个随机实验，通常有两个变体，A和B。利用控制变量法保持有单一变量的前提下，将A、B数据进行对比，得出实验结论。AB 是一种科学的利用数据证明方案可行性的手段，一般在网站中广泛使用。 通过abtest系统对迭代方案进行实验, 并结合数据进行分析，反向再验证和驱动方案，是一个发现问题、提出假设、印证猜想、不断优化的过程。 「合适的推荐方法是要经过不断的实验去验证」，验证的过程也是在校验数据，从而优化推荐系统策略，最终提升用户新增和留存。

▌2.1指标定义

在abtest前，我们需要梳理出我们关心的若干指标，并选择某个指标作为 「北极星指标」 ，如点击率、转化率、浏览时长、gmv、客单价等，未来讨论的推荐系统的相关优化也将围绕若干个目标进行。也有人将核心的指标成为北极星指标，北极星指标经常在 「增长黑客」 中被使用。来自微软Bing的例子:Bing希望优化长期查询份额（市场中的查询百分比）和长期收入。短期内，通过展示更多广告很容易赚钱，但它可能会损害用户体验。所以其实 「短期」 和 「长期」 指标的定义也很重要，如何通过abtest 「平衡和评估长短期收益」 。

▌2.2请了解几个事实

「不是每个想法都是好的、大部分想法都是不好的」 ；Many times, we have to tell people that their new beautiful baby is actually…ugly。

根据微软官方发布的上万次abtest实验数据来看

  1. 1/3 of ideas were positive ideas and statistically significant

  2. 1/3 of ideas were flat: no statistically significant difference

  3. 1/3 of ideas were negative and statistically significant

▌2.3实验管理平台

▏ 2.3.1实验报告

实验报告需要 「对脏数据进行过滤」 ，并做一定的 「效果平滑」 ，效果 「波动告警」 。异常值会产生明显的偏差: 足以导致错误的统计结果。例: 亚马逊上有围绕100,000名用户进行的abtest实验，其中2％的用户的客单价为30美元， 2％的用户客单价是1200美元，有时（很少）“用户”购买足以显着扭曲结果。

▏ 2.3.2分流&分层策略

如果流量不进行分层、分流可能会导致 「流量饥饿」 ，即实验一在进行中占用了全站的80%的流量，实验二就只能使用20%的流量。因此良好的分层、分流规则可以充分使用网站的流量。常见的分流策略有: Random – 随机分流，用于可变结果集,Partition By User – 「按用户切分」 ，同一用户永远看到同样结果,Partition By Category –  「按分类切分」 ，针对不同分类测试算法针对性。在分流的上层则会考虑分层，并且在互联网公司中应用广泛。

通常网站会利用分层和分流的机制保证本站的流量高可用，原因有以下几点：

1）网站的流量是 「有限」 的

2）实验的对象是多层的或同一层内 「互不干扰」 的。多层：例如网站不仅仅有UI层（界面），通常还有算法层等；同一层内互不干扰：例如网站的推荐位有多个（首页推荐位、商详页推荐位）。

3）AB tests的需求是大量的

注意点: 「幂等-均匀化-并行-互斥」 ; 分层实验，促进流量的 「最大化利用」。

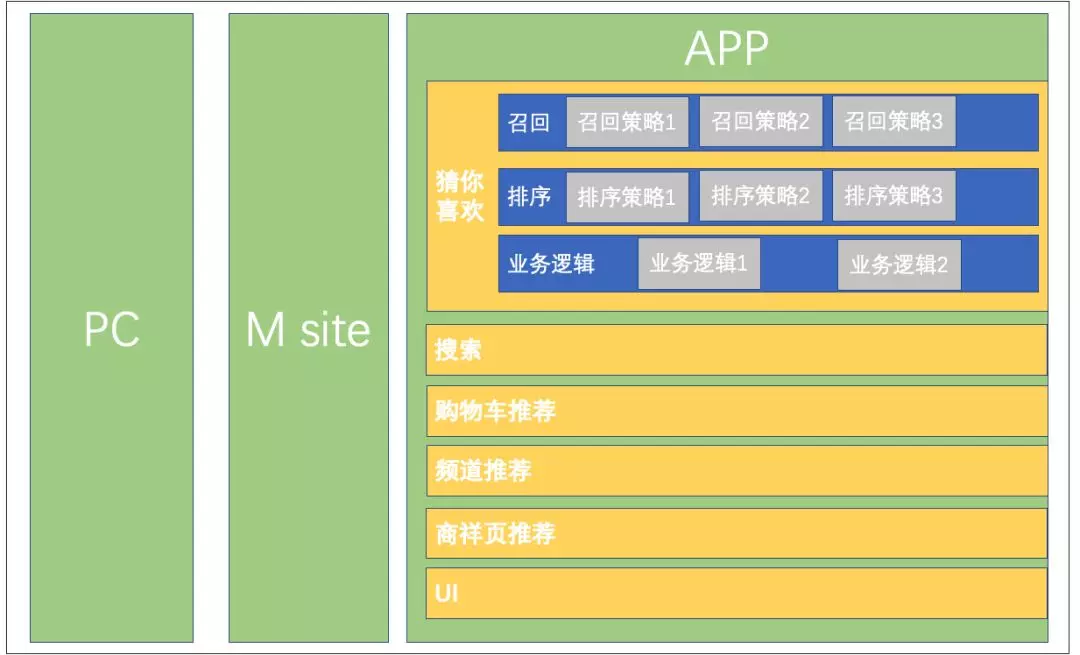
规则 1. 「正交、互斥」

在介绍分层规则之前，先介绍一下正交和互斥的概念。

1）正交，如何理解正交?

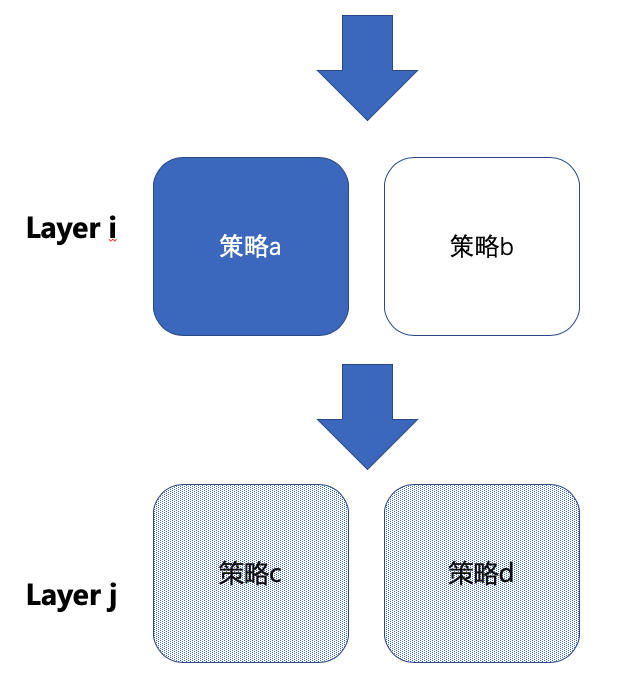
例如：我们有100个兵乓球，随机拿出来50个染成蓝色，50个染成白色，则我们有蓝色、白色兵乓球各50个，现在我们把这100个兵乓球重新放在袋子中摇匀，随机拿出50个兵乓球，那么这50个兵乓球颜色蓝色和白色各25。当然举这个例子并不是非常的恰当，因为样本太少了，此处举例只为说明正交的意义。

正交实验：每个独立实验为一层，层与层之间流量是 「正交」 的，一份流量穿越每层实验时，都会再次 「随机打散」 ，且 「随机效果离散」 。

  1. 互斥，如何理解互斥？

例如：我们有100个兵乓球，每25个为一组，分别染成蓝、白、橘、绿。若X实验拿的是蓝色、白色则Y实验只能拿橘色和绿色，我们说X实验的和Y实验是「」互斥的。

互斥实验： 「实验在同一层拆分流量，且不论如何拆分，不同组的流量是不重叠的」。

注:分流及分层实验设计 基于 「Goolge论文」: 《Overlapping Experiment Infrastructure:More, Better, Faster Experimentation》

流量从上往下流过分流模型：

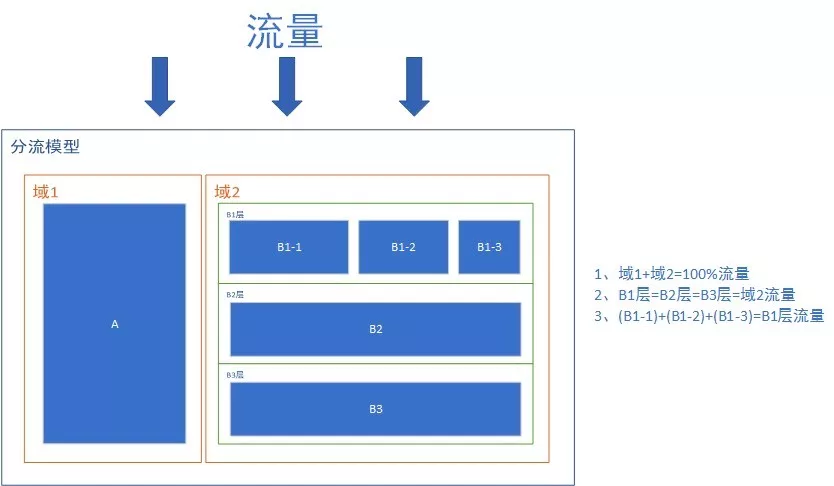
1）规则详述：

域1和域2拆分流量，此时域1和域2是互斥的。

流量流过域2中的B1层、B2层、B3层时，B1层、B2层、B3层的流量都是与域2的流量相等。此时B1层、B2层、B3层的流量是正交的。

扩展：流量流过域2中的B1层时，又把B1层分为了B1-1，B1-2，B1-3，此时B1-1，B1-2，B1-3之间又是互斥的。

根据以上规则我们可以不断的在此模型中增加**「域、层」 ，并且可以「互相嵌套」**。这要与实际的业务相匹配，拆分过多的结构可能会把简单的业务复杂化，拆分过少的结构又可能不满足实际业务。

2）使用场景

例1：B1层、B2层、B3层可能分别为：UI层、搜索结果层、广告结果层，这几层基本上是没有任何的业务关联度的，即使共用相同的流量（流量正交）也不会对实际的业务造成结果。但是如果不同层之间所进行的试验互相关联，如B1层是修改的一个页面的按钮文字颜色，B2层是修改的按钮的颜色，当按钮文字颜色和按钮颜色一样时，该按钮已经是不可用的了。因此建议同一类型的实验在同一层内进行，并且需要考虑到不同实验互相的依赖。

例2：域1的此种分流的意义在于，当我们做一个实验，并且希望其他任何实验都不能对我实验进行干扰，保证最后实验的**「可信度」**。

▏2.3.3AA/AB测试要点

1）候选策略+预测模型作为「最小的考察单元」

2）通过规则配置ABtest:配置流量切分，候选策略及预测模型

3） 「重视抽样误差」

4）关注**「时间周期效应」**

▏ 2.3.4流程

1） 「随机分组」(ABCDE…):A-控制组，与线上一致;B-测试组;C…

2） 「收集相关数据」(对决策有用的数据)

3） 「数据分析」，必须通过假设检验来确定差异不是来自于偶然，通过因果关系证明变化由测试桶的变化带来。

▌2.4 abtest 的那些技术

▏ 2.4.1为什么灵敏度(p-value)很重要

p-value即概率，反映某一事件发生的可能性大小，主要在abest中说明实验的提升的显著性，并且往往与假设检验相挂钩。统计学根据显著性检验方法所得到的P 值，一般以 「P < 0.05 为有统计学差异」 ， P<0.01 为有显著统计学差异，P<0.001为有极其显著的统计学差异。其含义是样本间的差异由抽样误差所致的概率小于0.05 、0.01、0.001。实际上， 「P值不能赋予数据任何重要性」 ，只能说明 「某事件发生的几率」 。在实践中建议，运行A / A测试，并同时也关注相关指标及p-value。 A / A测试中度量的P-value分布应该是统一的，进行1,000次A / A测试，并检查 「分布是否均匀」 ，当我们得到异常信息时，则需要纠正一些事情。

▏ 2.4.2假设检验

假设检验是推论统计中用于检验统计假设的一种方法。而“统计假设”是可通过观察一组随机变量的模型进行检验的科学假说。一旦能估计未知参数，就会希望根据结果对未知的真正参数值做出适当的推论。 统计上对参数的假设，就是对一个或多个参数的论述。而其中欲检验其正确性的为 「零假设」（null hypothesis），零假设通常由研究者决定，反映研究者对未知参数的看法。相对于零假设的其他有关参数之论述是 「备择假设」（alternative hypothesis），它通常反映了执行检定的研究者对参数可能数值的另一种（对立的）看法（换句话说，备择假设通常才是研究者最想知道的）。

常见假设检验的种类包括： 「t检验，Z检验，卡方检验，F检验」 等等。

▏ 2.4.3 t-test、z-test、p-value、ci(confidence interval)

1）T检验，亦称student t检验（Student’s t test），主要用于 「样本含量较小」（例如n<30）， 「总体标准差σ未知的正态分布」 资料。 T检验是用t分布理论来推论差异发生的概率，从而比较两个平均数的差异是否显著。t检验是对各回归系数的显著性所进行的检验，（－－这个太不全面了，这是指在多元回归分析中，检验回归系数是否为0的时候，先用F检验，考虑整体回归系数，再对每个系数是否为零进行t检验。t检验还可以用来检验样本为来自一元正态分布的总体的期望，即均值；和检验样本为来自二元正态分布的总体的期望是否相等） 未知，一般检验用T检验。

适用条件： 已知一个总体均数；可得到一个样本均数及该样本标准误； 样本来自正态或近似正态总体。

T的公式：T=(T-μ)/S/n的平方根

「若T值大于临界值，则拒绝原假设，否则不拒绝」。

2）Z检验是一般用于 「大样本」(即样本容量大于30)平均值差异性检验的方法。它是用 「标准正态分布」 的理论来推断差异发生的概率，从而比较两个平均数平均数的差异是否显著。 当已知标准差时，验证一组数的均值是否与某一期望值相等时，用Z检验。

Z检验的步骤 适用条件：已知一个总体均数；可得到一个样本均数及该样本标准误； 样本来自 「正态或近似正态总体」。

　　第一步：建立虚无假设，即先假定两个平均数之间没有显著差异，

　　第二步：计算统计量Z值，对于不同类型的问题选用不同的统计量计算方法，

　　如果检验一个样本平均数（x）与一个已知的总体平均数(μ0)的差异是否显著。其Z值计算公式为：

Z=（X-μ)/S/n的平方根

若Z值大于临界值，则认为为二者有差异，否�