作者：Alireza Dirafzoon

编译：ronghuaiyang

导读

在单 GPU 上就可以运行的 Transformer 模型，而且几乎不损失精度，了解一下？

如果你一直在开发机器学习算法用于处理连续数据 —— 例如语言处理中的文本，语音信号，或视频 —— 你可能听说过或使用过 Transformer，你可能知道这和是推特中认为的不同于一个东西。

图 1，打破僵局，摘自 Chris Manning 教授的推特

最近，谷歌推出了 Reformer 架构，Transformer 模型旨在有效地处理处理很长的时间序列的数据(例如，在语言处理多达 100 万个单词)。Reformer 的执行只需要更少的内存消耗，并且即使在单个 GPU 上运行也可以获得非常好的性能。论文 Reformer: The efficient Transformer 将在 ICLR 2020 上发表(并在评审中获得了近乎完美的分数)。Reformer 模型有望通过超越语言应用(如音乐、语音、图像和视频生成)对该领域产生重大影响。

在这篇文章中，我们将努力深入 Reformer 模型并试着去理解一些可视化方面的指南。准备好了吗？

为什么是 Transformer?

在 NLP 类的任务中，如机器翻译、文本生成、问答，可以被形式化为 sequence-to-sequence 的学习问题。长短期记忆(LSTM)神经网络，后来配备了注意机制，是著名用于构建预测模型等问题的架构，比如在谷歌的神经机器翻译系统中。然而，LSTMs 中递归的固有顺序特性使得无法并行化数据序列，因此在速度和梯度消失方有巨大的障碍，因此，这些架构无法在长序列上利用上下文。

最近 Transformer 模型，在 Attention is all you need 这篇文章中提出 —— 在许多任务达到了最先进的性能，摆脱了循环并引入了多头 self-attention 机制。Transformer 的主要新奇之处在于它的并行处理能力，这使得处理长序列(具有数千个单词的上下文窗口)成为可能，从而产生更优的模型，例如著名的 Open AI 的 GPT2 语言模型，而训练时间更少。Huggingface 的 Transformer 库 —— 具有超过 32 个预训练的语言模型，支持超过 100 种语言，并在 TensorFlow 和 PyTorch 进行了相互的转换，这在构建先进的 NLP 系统上是非常了不起的工作。Transformer 已经被用于除文本之外的应用上，比如生成音乐和图像。

Transformer 缺了点什么？

在深入研究 reformer 之前，让我们回顾一下 Transformer 模型的挑战之处。这需要对 transformer 体系结构本身有一定的了解，在这篇文章中我们无法一一介绍。然而，如果你还不知道，Jay Alamar 的 The Illustrated Transformer： http://jalammar.github.io/transformer/ 是迄今为止最好的可视化解释，我强烈建议在阅读本文其余部分之前先阅读他的文章。

尽管 transformer 模型可以产生非常好的结果，被用于越来越多的长序列，例如 11k 大小的文本，许多这样的大型模型只能在大型工业计算平台上训练，在单个 GPU 上一步也跑不了，因为它们的内存需求太大了。例如，完整的 GPT-2 模型大约包含 1.5B 参数。最大配置的参数数量超过每层 0.5B，而层数有 64 层。

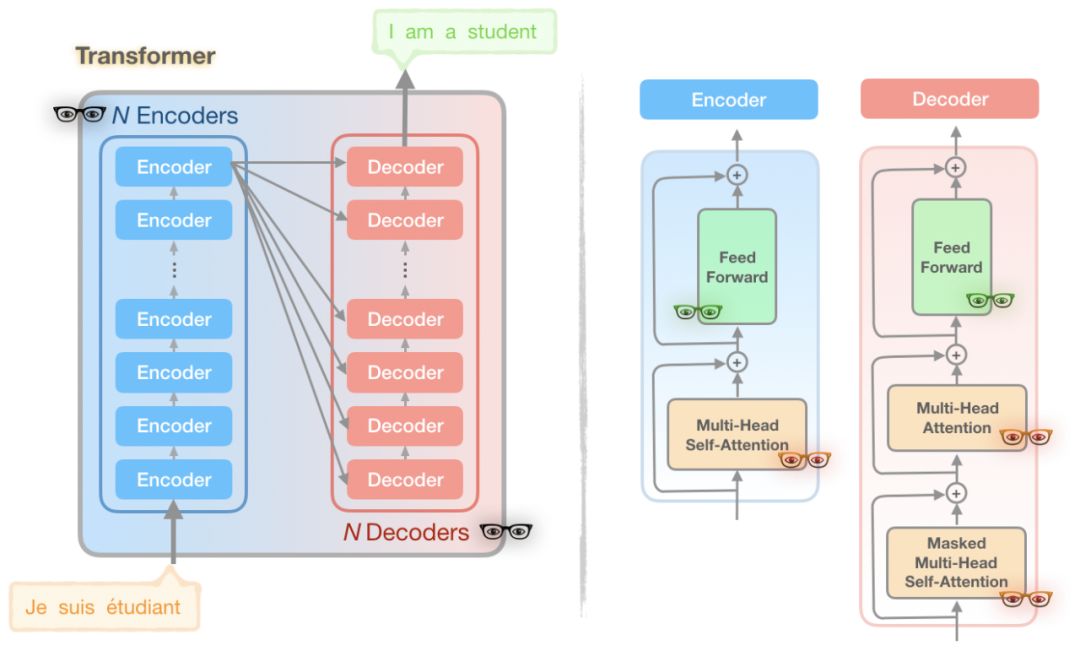
图 2：标准 Transformer 模型的简化图

如果这个模型看起来不熟悉或似乎很难理解，我劝你们暂停在这里回顾一下 Transformer。

你可能会注意到在图中存在一些 👓，有 3 种不同的颜色。这些独特的 👓的代表了 Transformer 模型的一部分，Reformer 作者发现了计算和内存问题的来源：

👀 问题 1 (红色 👓): 注意力计算

计算关注序列的长度 L 的复杂度是 O (L ²)(时间和内存)。想象一下如果我们有一个长度为 64K 的序列会发生什么。

👀 问题 2 (黑色 👓): 层数多

具有 N 层的模型要消耗 N 倍于单层模型的内存，因为每一层中的激活都需要存储以进行反向传播。

👀 问题 3 (绿色 👓): 前馈网络的深度

中间前馈层的深度往往比注意里激活的深度大得多。Reformer 模型解决了 Transformer 中上述三个内存消耗的主要来源，并对它们进行了改进，使 Reformer 模型能够处理最多 100 万单词的上下文窗口，所有这些都在单个 GPU 上，并且仅使用 16GB 内存。

简而言之，Reformer 模型结合了两种技术来解决注意力问题和内存分配：局部敏感哈希来减少长序列注意力的复杂度，可逆残差层更有效的利用内存。

下面我们进入进一步的细节。

💥 1. 局部敏感哈希(LSH) 注意力

💭 注意力以及最近的邻居

在深度学习中，注意力是一种机制，它使网络能够根据上下文的不同部分与当前时间步长之间的相关性，将注意力集中在上下文的不同部分。transformer 模型中存在三种注意机制：

图 3：在 Transformer 模型三种类型的注意力

在 Transformer 中使用的标准注意里是缩放的点积，表示为：

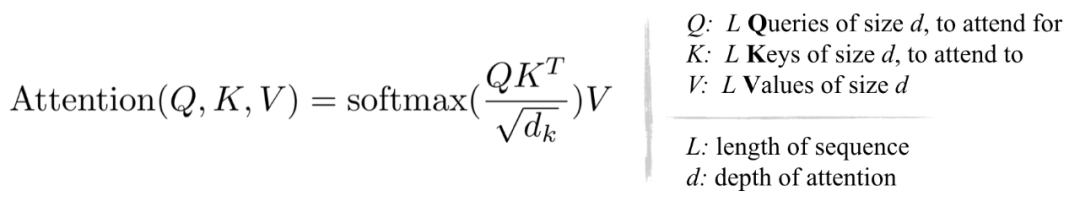
从上面的方程和下面的图，它可以观察到，QK ᵀ的计算和内存的消耗都是 O (L ²) 复杂度的，这是主要的内存瓶颈。

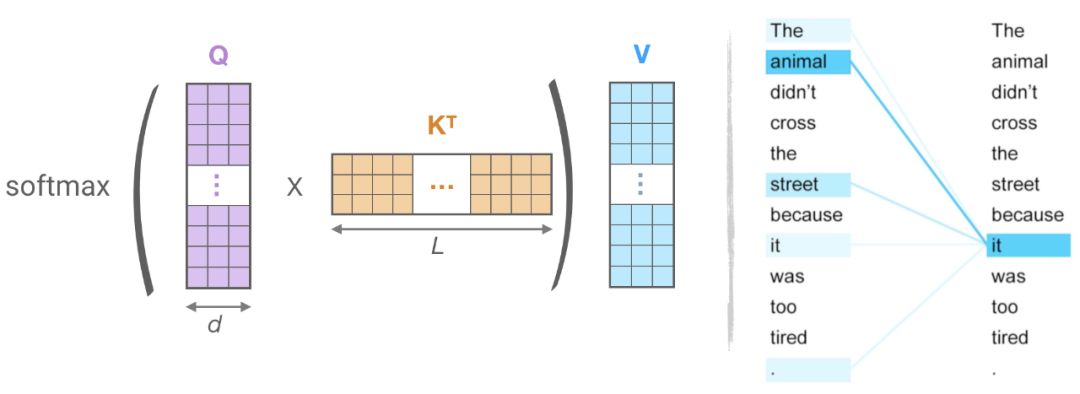
图 4：(左)：点积注意力的主要计算，(右)token(“it”)对于序列(“the”、“animal”、“street”、“it”、“it”)的注意力子集。

但这是计算和存储完整的矩阵 QK ᵀ是必要的吗 ?答案是不， , 我们感兴趣的是 softmax*( QK ᵀ )，它是由最大的元素决定的，通常是稀疏矩阵。因此，正如你在上面的示例中所看到的，对于每个查询 q，我们只需要注意最接近 q 的键 k。例如，如果长度是 64K，对于每个 q，我们可以只考虑 32 或 64 个最近的键的一个小子集。因此，注意力机制查找 query 的最近邻居键，但效率不高。这是不是让你想起了最近邻搜索？

Reformer 的第一个革新点来自用局部敏感哈希代替点积注意力，把复杂度从 O(L ²)变为了 O(L log L)。

🗒 LSH 的最近邻搜索

LSH 是一种著名的算法，它在高维数据集中以一种“高效”和“近似”的方式搜索“最近的邻居”。LSH 背后的主要思想是选择 hash 函数，对于两个点 p 和 q，如果 q 接近 p，那么很有可能我们有 hash(q) == hash(p) 。

做到这一点最简单的方法是用随机超平面不断的分割空间，并在每个点上加上 sign(p ᵀH)作为 hash 码。让我们来看一个例子：

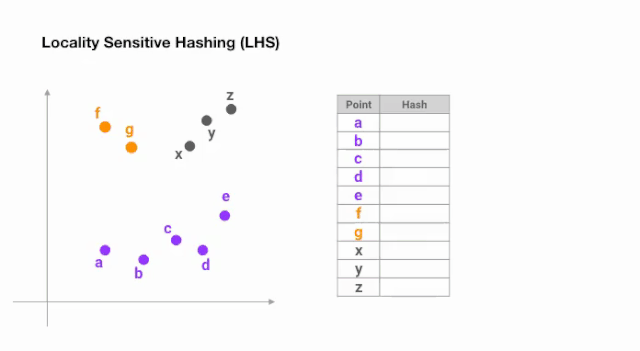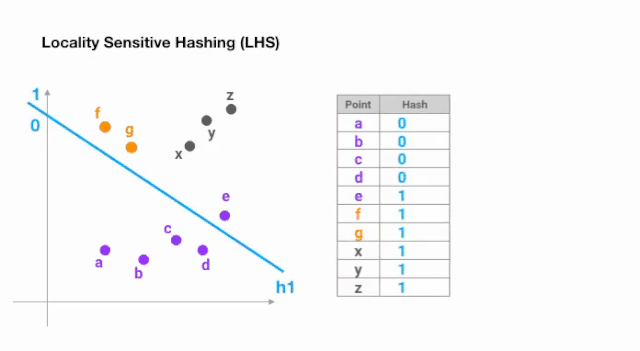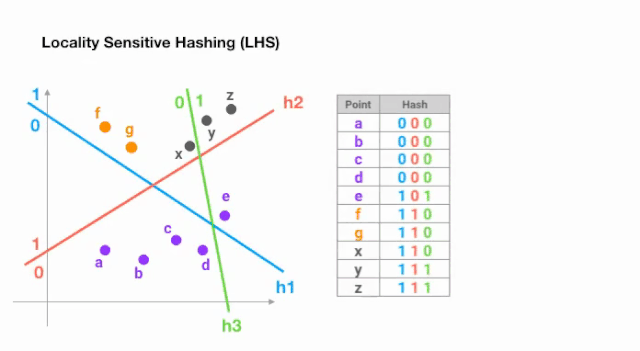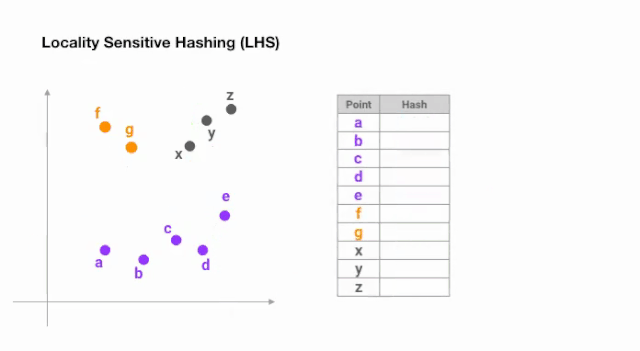
图 5：用于最近邻搜索的局部敏感哈希的简化动画

一旦我们找到所需长度的哈希码，我们就根据它们的哈希码将这些点分成桶 —— 在上面的例子中，a 和 b 属于同一个桶，因为 hash(a) == hash(b)。现在，查找每个点的最近邻居的搜索空间大大减少了，从整个数据集到它所属的桶中。

Angular LSH：普通 LSH 的一个变化，成为 Angular LSH，使用不同的编码把点投影到单位球上预先定义好的区域里。然后一系列随机旋转的点定义了这些点所属的桶。让我们通过一个简单的 2D 例子来说明这一点，这个例子来自于 Reformer 的论文：

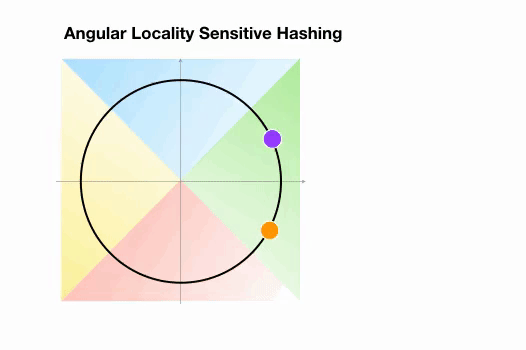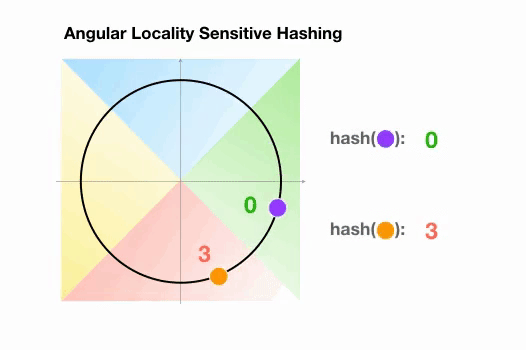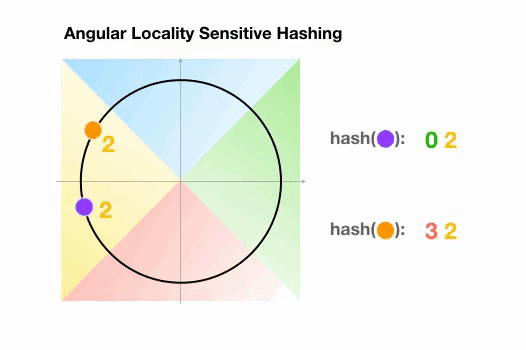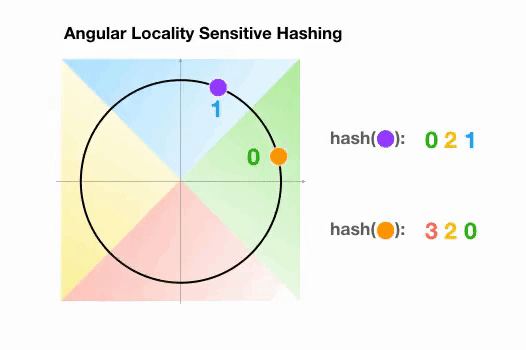
图 6：Angular LSH 最近邻搜索的简化动画，两个点在不同的桶

这里我们有两个点，它们投影到一个单位圆上，并随机旋转 3 次，角度不同。我们可以观察到，它们不太可能共享同一个 hash 桶。在下一个例子中，我们可以看到两个非常接近的点在 3 次随机循环后将共享相同的 hash 桶：

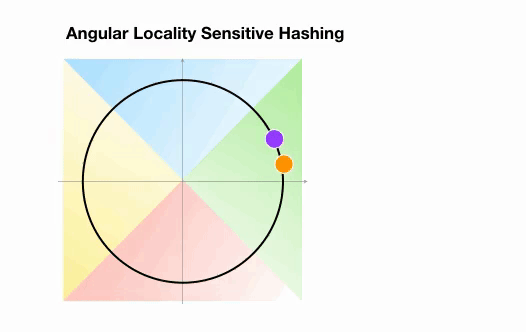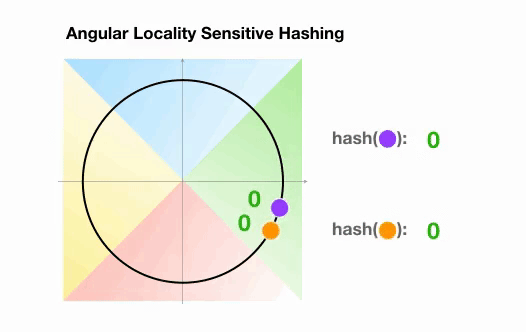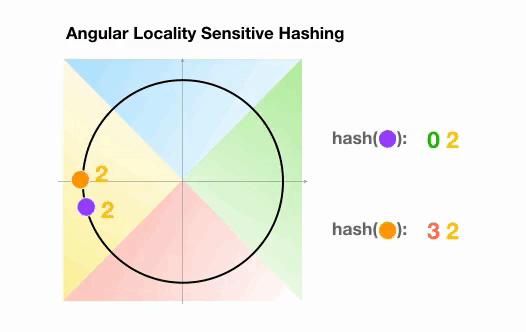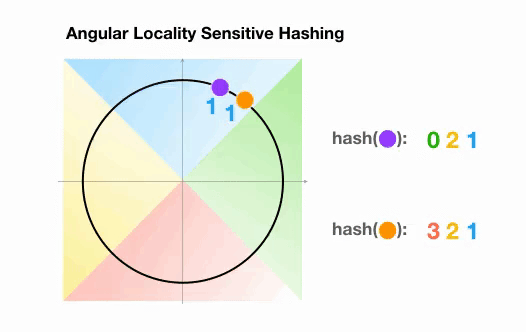
图 7：Angular LSH 最近邻搜索的简化动画：两个点很近

🚀 LSH 注意力

下面是 LSH 注意力背后的基本思想。回顾一下上面的标准注意力公式，我们不计算 Q 和 K 矩阵中所有向量的注意力，而是做以下工作：

  • 找到 Q 和 K 矩阵的 LSH 散列。

  • 只计算相同哈希桶中的 k 和 q 向量的标准注意力值。

多回合的 LSH 注意力：重复以上步骤几次，以增加相似的物品落入相同的桶中的概率。

下面的动画演示了一个 LSH 注意力的简化版本。

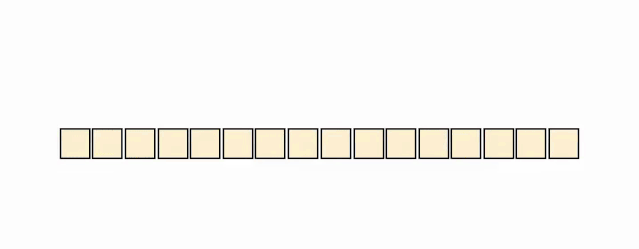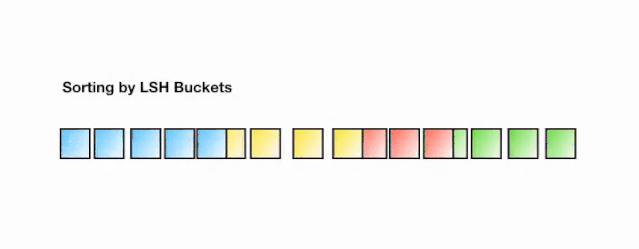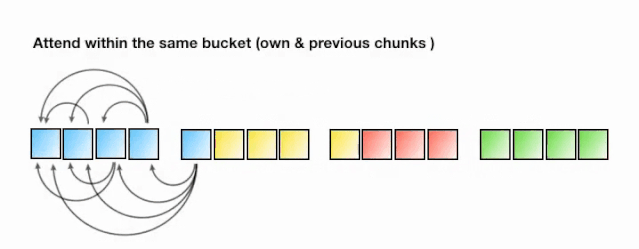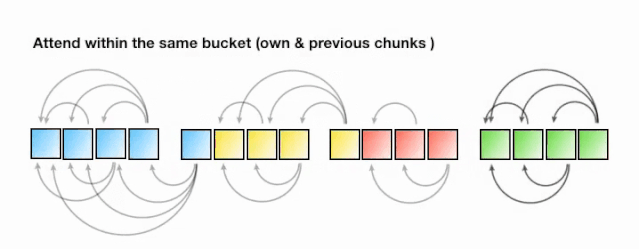
图 6：LSH 注意机制的简化示意图

💥 2. 可逆 Transformer 和分块

现在我们准备解决 Transformer 的第二个和第三个问题，即大量的( N)编码器和解码器层以及前馈层的深度。

🗒 可逆残差网络(RevNet)

仔细观察图 2 中的编码器和解码器块，我们发现每个注意力层和前馈层都被包装成一个残差块(类似于图 6(左)所示)。残差网络*(*ResNets)，是用来帮助解决深层网络(多层)中的消失梯度问题的强大组件。然而，ResNets 的内存消耗是一个瓶颈，因为需要在内存中存储每一层的激活来计算反向传播期间的梯度。内存成本与网络中的单元数量成正比。

为了解决这个问题，由一系列可逆块组成的[可逆残差网络(RevNet)]( https://papers.nips.cc/paper/6816reversib-resinetworkworkbackwithoutoutstorings -activations.pdf)。在 Revnet 中，每一层的激活都可以从后续层的激活中精确地重建，这使得我们可以在不将激活存储在内存的情况下执行反向传播。图 6 表示了残差块和可逆残差块。注意我们如何从它的输出(Y ₁, Y ₂)计算物体的输入(X ₁, X ₂)。

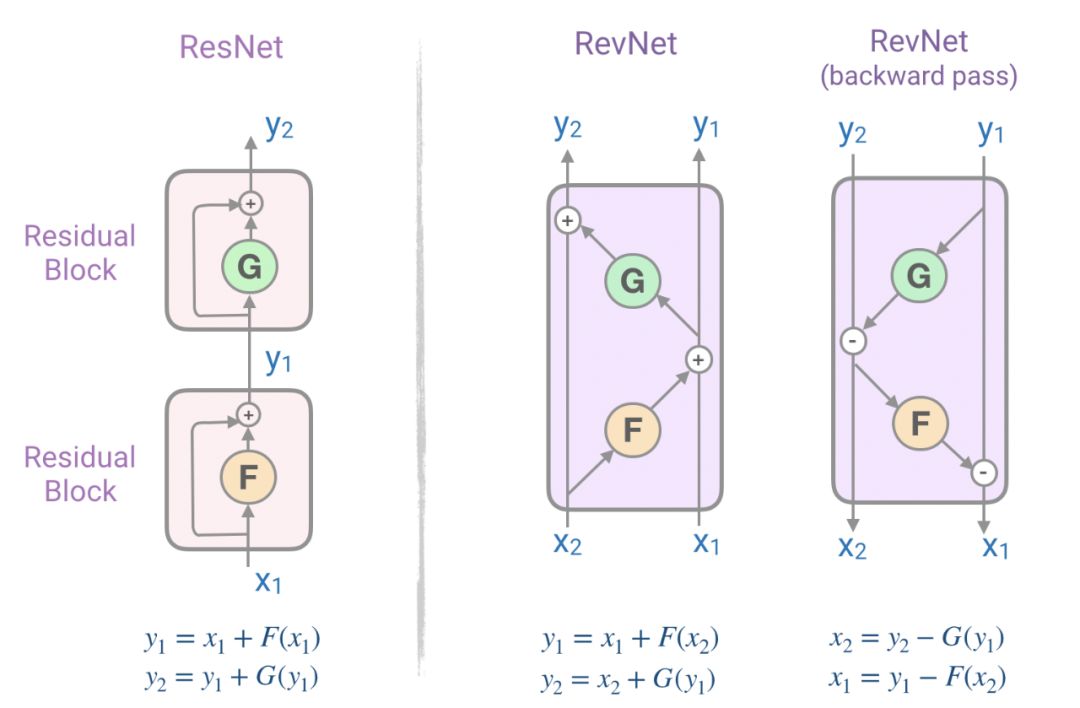
图 6：残差网络块(左)和可逆残差块(右)

🚀 可逆 Transformer

回到我们的第二个问题，这个问题是处理 N 层 Transformer 网络的内存需求 —— 可能会有非常大的 N。Reformer 将 RevNet 思想应用于变压器，将 RevNet 块内的注意力层和前馈层结合起来。在图 6 中，现在 F 为注意层， G 为前馈层：

Y ₁= X ₁+Attention(X ₂) Y ₂= X ₂+FeedForward(Y ₁)

🎉现在使用可逆的残差层代替标准残差层使得在训练过程中只需要存储激活一次，不是 N 次。

🚀 分块

在 Reformer 的效率改进的最后一部分处理第三个问题，即前馈层的高维中间向量 — 可以达到 4K 和更高的维度。由于前馈层的计算是独立于序列的各个位置的，所以前向和后向的计算以及反向的计算都可以被分割成块。例如，对于向前传递，我们将有：

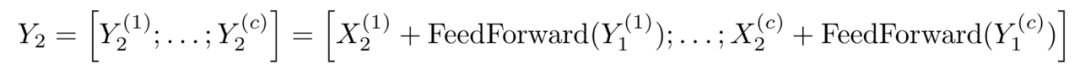
前向通道计算中的分块

🚀 实验结果

作者分别对图像生成任务 imagenet64(长度为 12K)和文本任务 enwik8(长度为 64K)进行了实验，评价了可逆 Transformer 和 LSH 哈希对内存、精度和速度的影响。

🎉可逆 Transformer 匹配基准：他们的实验结果表明，可逆的 Transformer 可以节省内存不牺牲精度：

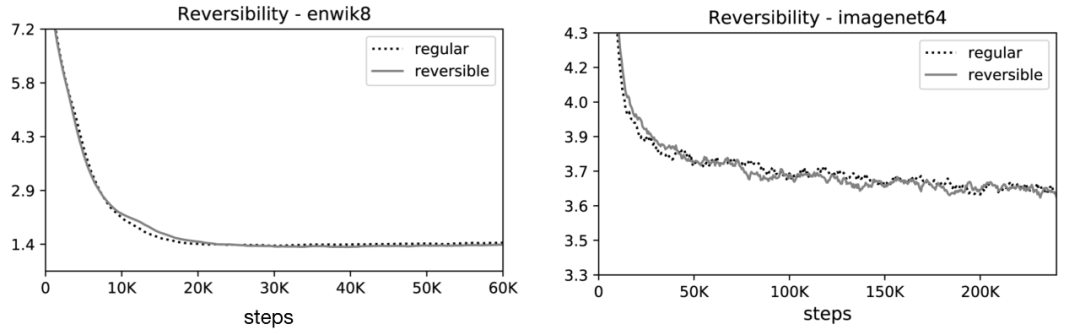
在 enwik8 和 imagenet64 训练中，可逆性对性能的影响

🎉LSH 注意力匹配基准：📔注意 LSH 注意力是一个近似的全注意力，其准确性随着散列值的增加而提高。当哈希值为