大数据文摘与百度NLP联合出品

编译：张驰、毅航、Conrad、龙心尘

编者按：前一段时间谷歌推出的BERT模型在11项NLP任务中夺得STOA结果，引爆了整个NLP界。而BERT取得成功的一个关键因素是Transformer的强大作用。谷歌的Transformer模型最早是用于机器翻译任务，当时达到了STOA效果。Transformer改进了RNN最被人诟病的训练慢的缺点，利用self-attention机制实现快速并行。并且Transformer可以增加到非常深的深度，充分发掘DNN模型的特性，提升模型准确率。在本文中，我们将研究Transformer模型，把它掰开揉碎，理解它的工作原理。

以下是正文，请欣赏：

Transformer由论文《Attention is All You Need》提出，现在是谷歌云TPU推荐的参考模型。论文相关的Tensorflow的代码可以从GitHub获取，其作为Tensor2Tensor包的一部分。哈佛的NLP团队也实现了一个基于PyTorch的版本，并注释该论文。

在本文中，我们将试图把模型简化一点，并逐一介绍里面的核心概念，希望让普通读者也能轻易理解。

Attention is All You Need：

https://arxiv.org/abs/1706.03762

从宏观的视角开始

首先将这个模型看成是一个黑箱操作。在机器翻译中，就是输入一种语言，输出另一种语言。

那么拆开这个黑箱，我们可以看到它是由编码组件、解码组件和它们之间的连接组成。

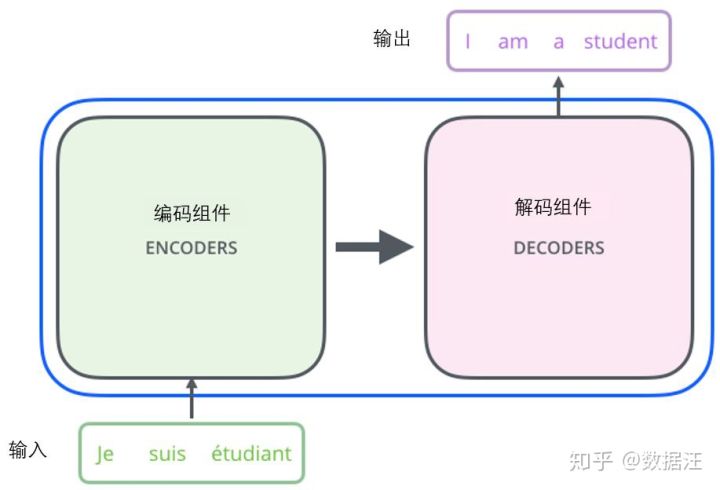
编码组件部分由一堆编码器（encoder）构成（论文中是将6个编码器叠在一起——数字6没有什么神奇之处，你也可以尝试其他数字）。解码组件部分也是由相同数量（与编码器对应）的解码器（decoder）组成的。

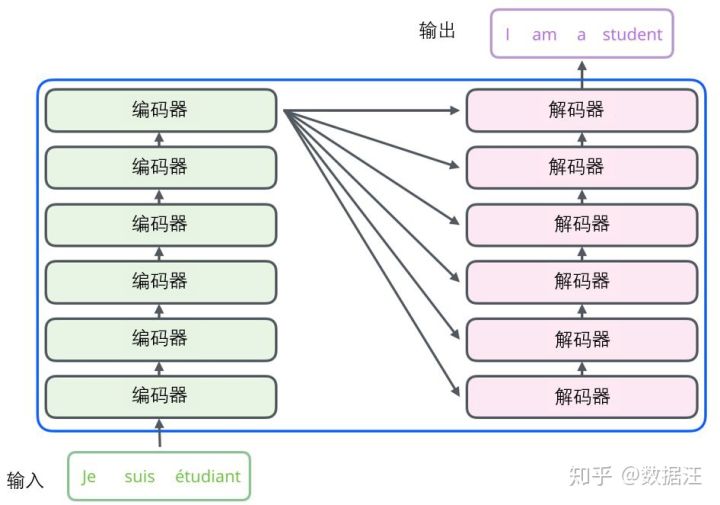
所有的编码器在结构上都是相同的，但它们没有共享参数。每个解码器都可以分解成两个子层。

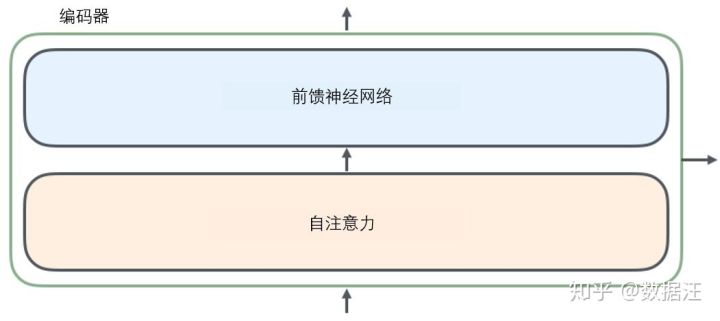
从编码器输入的句子首先会经过一个自注意力（self-attention）层，这层帮助编码器在对每个单词编码时关注输入句子的其他单词。我们将在稍后的文章中更深入地研究自注意力。

自注意力层的输出会传递到前馈（feed-forward）神经网络中。每个位置的单词对应的前馈神经网络都完全一样（译注：另一种解读就是一层窗口为一个单词的一维卷积神经网络）。

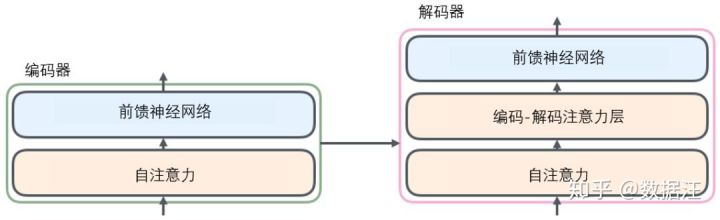
解码器中也有编码器的自注意力（self-attention）层和前馈（feed-forward）层。除此之外，这两个层之间还有一个注意力层，用来关注输入句子的相关部分（和seq2seq模型的注意力作用相似）。

将张量引入图景

我们已经了解了模型的主要部分，接下来我们看一下各种向量或张量（译注：张量概念是矢量概念的推广，可以简单理解矢量是一阶张量、矩阵是二阶张量。）是怎样在模型的不同部分中，将输入转化为输出的。

像大部分NLP应用一样，我们首先将每个输入单词通过词嵌入算法转换为词向量。

每个单词都被嵌入为512维的向量，我们用这些简单的方框来表示这些向量。

词嵌入过程只发生在最底层的编码器中。所有的编码器都有一个相同的特点，即它们接收一个向量列表，列表中的每个向量大小为512维。在底层（最开始）编码器中它就是词向量，但是在其他编码器中，它就是下一层编码器的输出（也是一个向量列表）。向量列表大小是我们可以设置的超参数——一般是我们训练集中最长句子的长度。

将输入序列进行词嵌入之后，每个单词都会流经编码器中的两个子层。

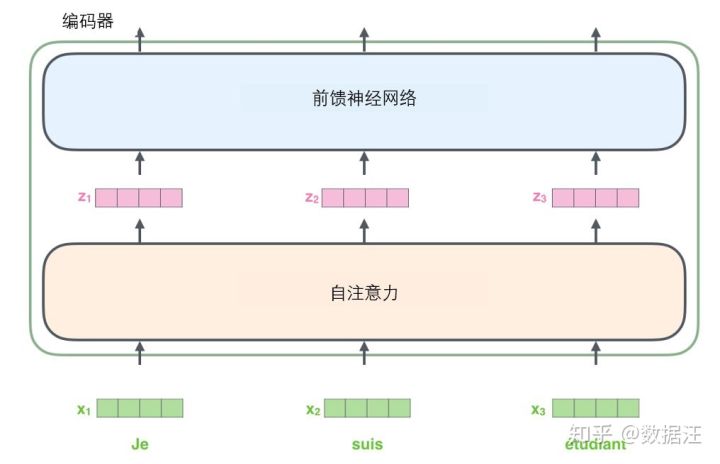
接下来我们看看Transformer的一个核心特性，在这里输入序列中每个位置的单词都有自己独特的路径流入编码器。在自注意力层中，这些路径之间存在依赖关系。而前馈（feed-forward）层没有这些依赖关系。因此在前馈（feed-forward）层时可以并行执行各种路径。

然后我们将以一个更短的句子为例，看看编码器的每个子层中发生了什么。

现在我们开始“编码”

如上述已经提到的，一个编码器接收向量列表作为输入，接着将向量列表中的向量传递到自注意力层进行处理，然后传递到前馈神经网络层中，将输出结果传递到下一个编码器中。

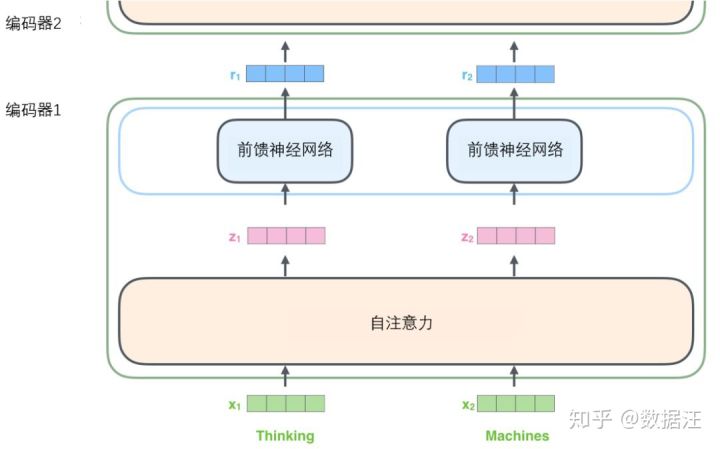
输入序列的每个单词都经过自编码过程。然后，他们各自通过前向传播神经网络——完全相同的网络，而每个向量都分别通过它。

从宏观视角看自注意力机制

不要被我用自注意力这个词弄迷糊了，好像每个人都应该熟悉这个概念。其实我之也没有见过这个概念，直到读到Attention is All You Need 这篇论文时才恍然大悟。让我们精炼一下它的工作原理。

例如，下列句子是我们想要翻译的输入句子：

The animal didn’t cross the street because it was too tired

这个“it”在这个句子是指什么呢？它指的是street还是这个animal呢？这对于人类来说是一个简单的问题，但是对于算法则不是。

当模型处理这个单词“it”的时候，自注意力机制会允许“it”与“animal”建立联系。

随着模型处理输入序列的每个单词，自注意力会关注整个输入序列的所有单词，帮助模型对本单词更好地进行编码。

如果你熟悉RNN（循环神经网络），回忆一下它是如何维持隐藏层的。RNN会将它已经处理过的前面的所有单词/向量的表示与它正在处理的当前单词/向量结合起来。而自注意力机制会将所有相关单词的理解融入到我们正在处理的单词中。

当我们在编码器#5（栈中最上层编码器）中编码“it”这个单词的时，注意力机制的部分会去关注“The Animal”，将它的表示的一部分编入“it”的编码中。

请务必检查Tensor2Tensor notebook ，在里面你可以下载一个Transformer模型，并用交互式可视化的方式来检验。

从微观视角看自注意力机制

首先我们了解一下如何使用向量来计算自注意力，然后来看它实怎样用矩阵来实现。

计算自注意力的第一步就是从每个编码器的输入向量（每个单词的词向量）中生成三个向量。也就是说对于每个单词，我们创造一个查询向量、一个键向量和一个值向量。这三个向量是通过词嵌入与三个权重矩阵后相乘创建的。

可以发现这些新向量在维度上比词嵌入向量更低。他们的维度是64，而词嵌入和编码器的输入/输出向量的维度是512. 但实际上不强求维度更小，这只是一种基于架构上的选择，它可以使多头注意力（multiheaded attention）的大部分计算保持不变。

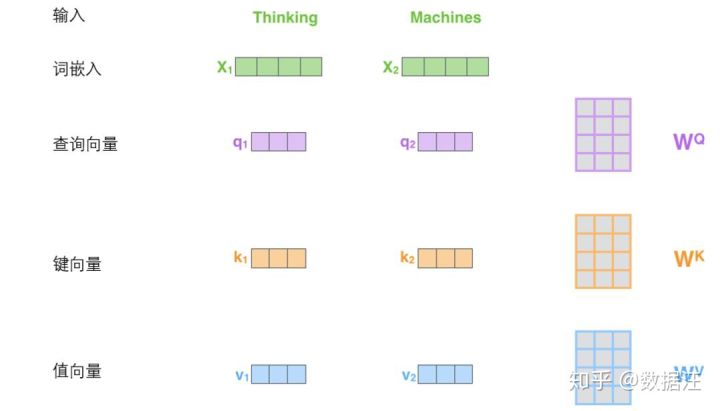
X1与WQ权重矩阵相乘得到q1, 就是与这个单词相关的查询向量。最终使得输入序列的每个单词的创建一个查询向量、一个键向量和一个值向量。

什么是查询向量、键向量和值向量向量？

它们都是有助于计算和理解注意力机制的抽象概念。请继续阅读下文的内容，你就会知道每个向量在计算注意力机制中到底扮演什么样的角色。

计算自注意力的第二步是计算得分。假设我们在为这个例子中的第一个词“Thinking”计算自注意力向量，我们需要拿输入句子中的每个单词对“Thinking”打分。这些分数决定了在编码单词“Thinking”的过程中有多重视句子的其它部分。

这些分数是通过打分单词（所有输入句子的单词）的键向量与“Thinking”的查询向量相点积来计算的。所以如果我们是处理位置最靠前的词的自注意力的话，第一个分数是q1和k1的点积，第二个分数是q1和k2的点积。

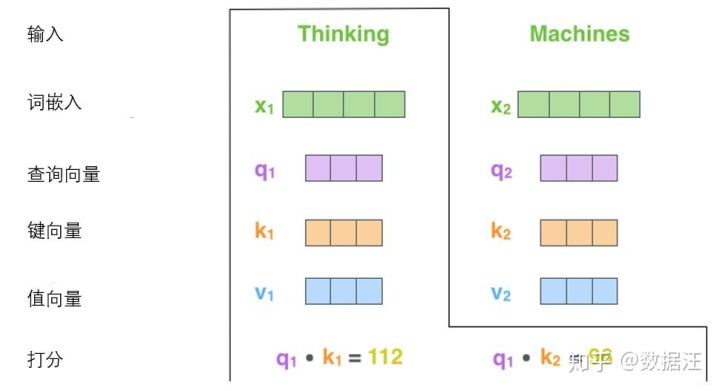
第三步和第四步是将分数除以8(8是论文中使用的键向量的维数64的平方根，这会让梯度更稳定。这里也可以使用其它值，8只是默认值)，然后通过softmax传递结果。softmax的作用是使所有单词的分数归一化，得到的分数都是正值且和为1。

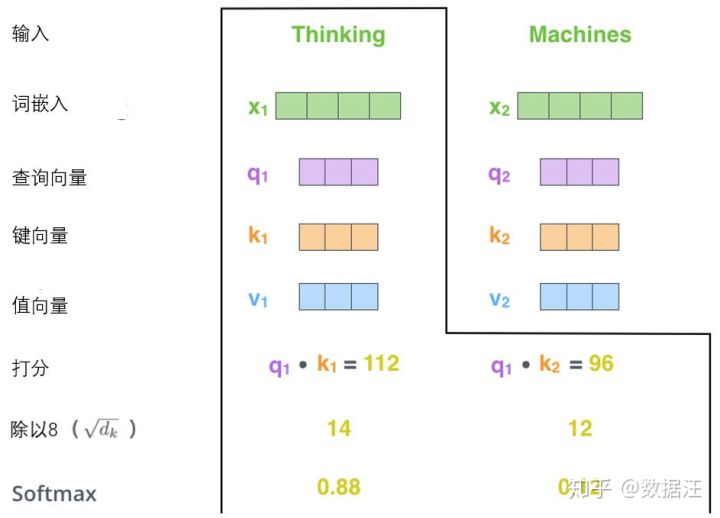
这个softmax分数决定了每个单词对编码当下位置（“Thinking”）的贡献。显然，已经在这个位置上的单词将获得最高的softmax分数，但有时关注另一个与当前单词相关的单词也会有帮助。

第五步是将每个值向量乘以softmax分数(这是为了准备之后将它们求和)。这里的直觉是希望关注语义上相关的单词，并弱化不相关的单词(例如，让它们乘以0.001这样的小数)。

第六步是对加权值向量求和（译注：自注意力的另一种解释就是在编码某个单词时，就是将所有单词的表示（值向量）进行加权求和，而权重是通过该词的表示（键向量）与被编码词表示（查询向量）的点积并通过softmax得到。），然后即得到自注意力层在该位置的输出(在我们的例子中是对于第一个单词)。

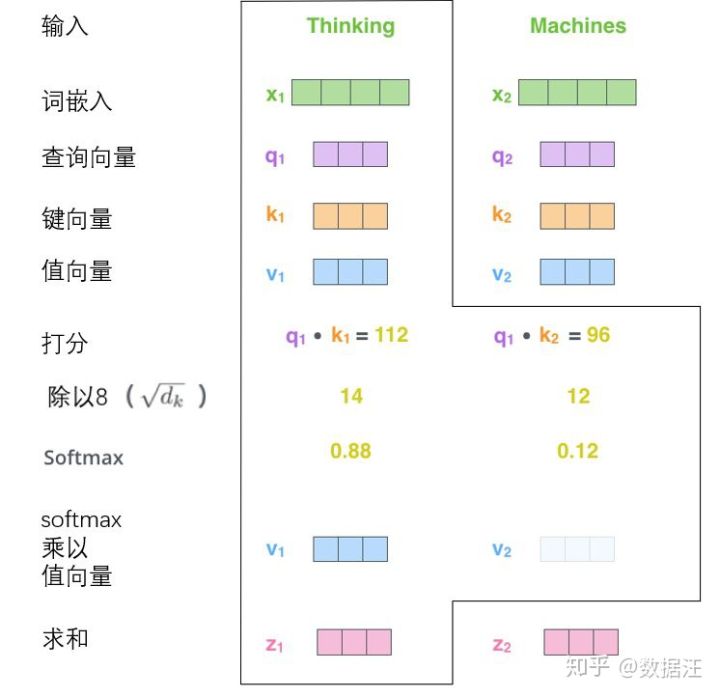
这样自自注意力的计算就完成了。得到的向量就可以传给前馈神经网络。然而实际中，这些计算是以矩阵形式完成的，以便算得更快。那我们接下来就看看如何用矩阵实现的。

通过矩阵运算实现自注意力机制

第一步是计算查询矩阵、键矩阵和值矩阵。为此，我们将将输入句子的词嵌入装进矩阵X中，将其乘以我们训练的权重矩阵(WQ，WK，WV)。

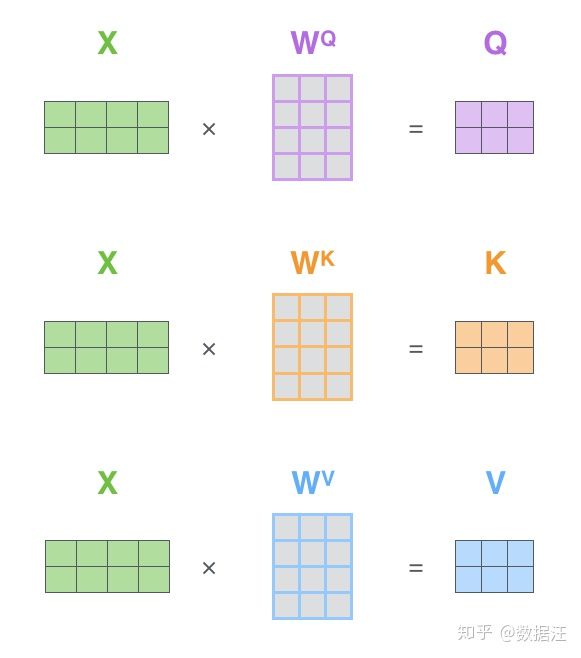
x矩阵中的每一行对应于输入句子中的一个单词。我们再次看到词嵌入向量 (512，或图中的4个格子)和q/k/v向量(64，或图中的3个格子)的大小差异。

最后，由于我们处理的是矩阵，我们可以将步骤2到步骤6合并为一个公式来计算自注意力层的输出。

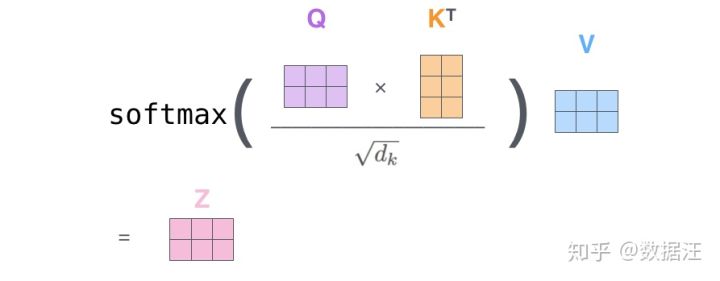
自注意力的矩阵运算形式

“大战多头怪”

通过增加一种叫做“多头”注意力（“multi-headed” attention）的机制，论文进一步完善了自注意力层，并在两方面提高了注意力层的性能：

1.它扩展了模型专注于不同位置的能力。在上面的例子中，虽然每个编码都在z1中有或多或少的体现，但是它可能被实际的单词本身所支配。如果我们翻译一个句子，比如“The animal didn’t cross the street because it was too tired”，我们会想知道“it”指的是哪个词，这时模型的“多头”注意机制会起到作用。

2.它给出了注意力层的多个“表示子空间”（representation subspaces）。接下来我们将看到，对于“多头”注意机制，我们有多个查询/键/值权重矩阵集(Transformer使用八个注意力头，因此我们对于每个编码器/解码器有八个矩阵集合)。这些集合中的每一个都是随机初始化的，在训练之后，每个集合都被用来将输入词嵌入(或来自较低编码器/解码器的向量)投影到不同的表示子空间中。

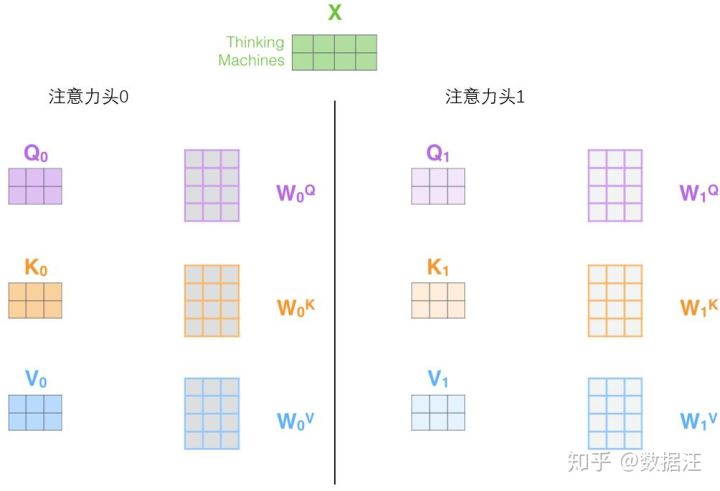
在“多头”注意机制下，我们为每个头保持独立的查询/键/值权重矩阵，从而产生不同的查询/键/值矩阵。和之前一样，我们拿X乘以WQ/WK/WV矩阵来产生查询/键/值矩阵。

如果我们做与上述相同的自注意力计算，只需八次不同的权重矩阵运算，我们就会得到八个不同的Z矩阵。

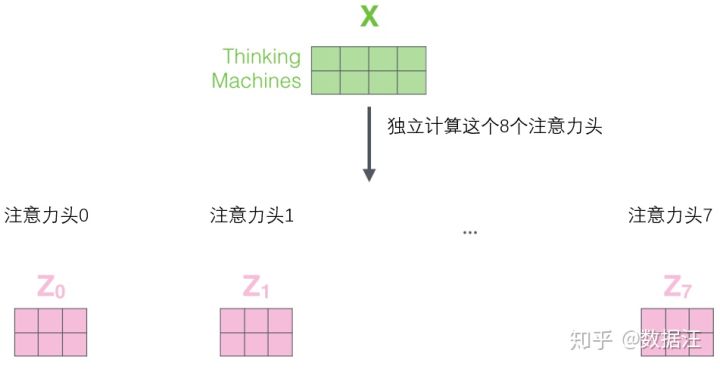
这给我们带来了一点挑战。前馈层不需要8个矩阵，它只需要一个矩阵(由每一个单词的表示向量组成)。所以我们需要一种方法把这八个矩阵压缩成一个矩阵。那该怎么做？其实可以直接把这些矩阵拼接在一起，然后用一个附加的权重矩阵WO与它们相乘。

这几乎就是多头自注意力的全部。这确实有好多矩阵，我们试着把它们集中在一个图片中，这样可以一眼看清。

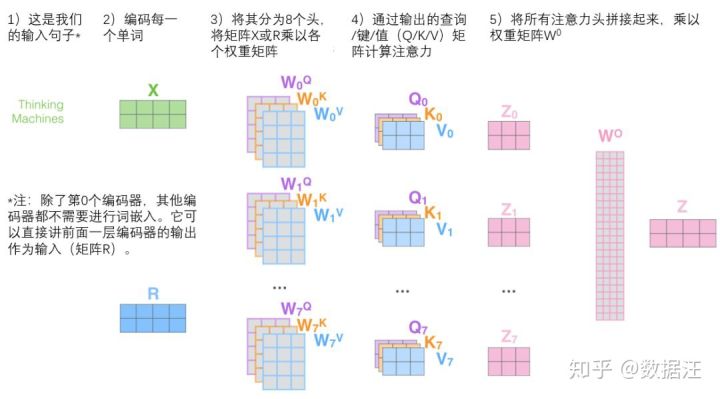
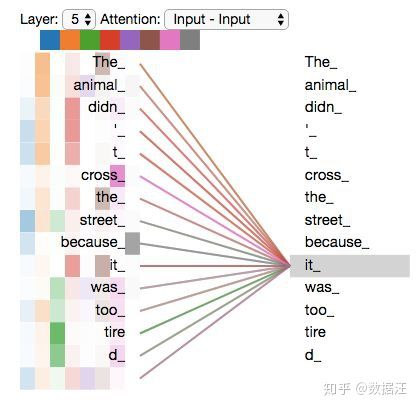
既然我们已经摸到了注意力机制的这么多“头”，那么让我们重温之前的例子，看看我们在例句中编码“it”一词时，不同的注意力“头”集中在哪里：

当我们编码“it”一词时，一个注意力头集中在“animal”上，而另一个则集中在“tired”上，从某种意义上说，模型对“it”一词的表达在某种程度上是“animal”和“tired”的代表。

然而，如果我们把所有的attention都加到图示里，事情就更难解释了：

使用位置编码表示序列的顺序

到目前为止，我们对模型的描述缺少了一种理解输入单词顺序的方法。

为了解决这个问题，Transformer为每个输入的词嵌入添加了一个向量。这些向量遵循模型学习到的特定模式，这有助于确定每个单词的位置，或序列中不同单词之间的距离。这里的直觉是，将位置向量添加到词嵌入中使得它们在接下来的运算中，能够更好地表达的词与词之间的距离。

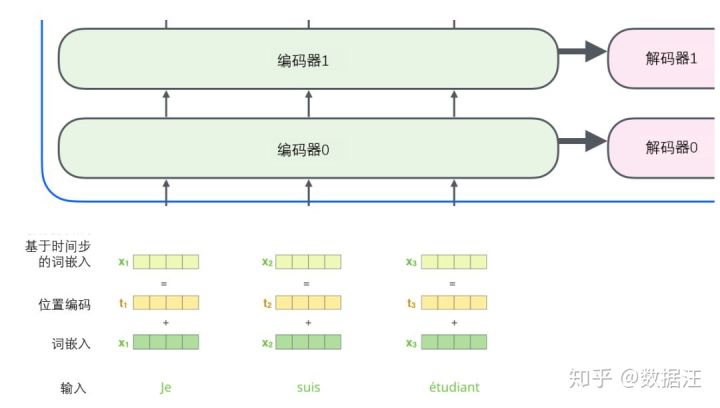
为了让模型理解单词的顺序，我们添加了位置编码向量，这些向量的值遵循特定的模式。

如果我们假设词嵌入的维数为4，则实际的位置编码如下：

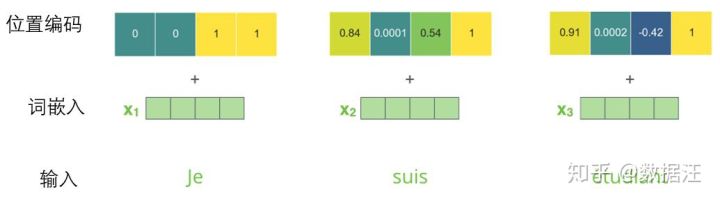
尺寸为4的迷你词嵌入位置编码实例

这个模式会是什么样子？

在下图中，每一行对应一个词向量的位置编码，所以第一行对应着输入序列的第一个词。每行包含512个值，每个值介于1和-1之间。我们已经对它们进行了颜色编码，所以图案是可见的。

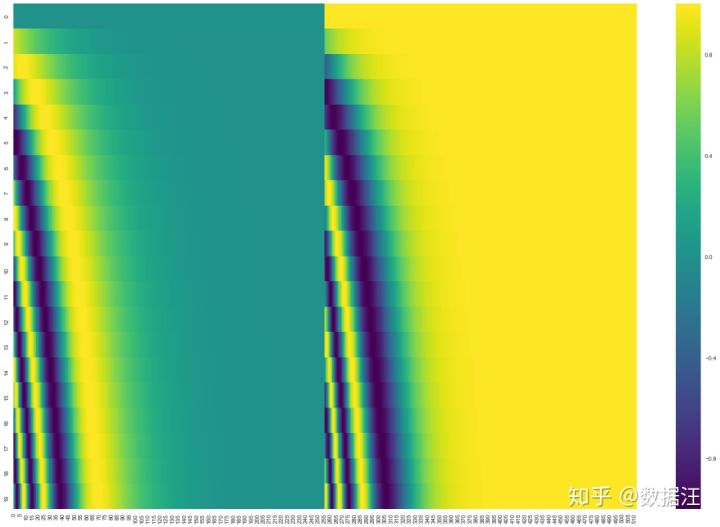
20字(行)的位置编码实例，词嵌入大小为512(列)。你可以看到它从中间分裂成两半。这是因为左半部分的值由一个函数(使用正弦)生成，而右半部分由另一个函数(使用余弦)生成。然后将它们拼在一起而得到每一个位置编码向量。

原始论文里描述了位置编码的公式(第3.5节)。你可以在 get_timing_signal_1d()中看到生成位置编码的代码。这不是唯一可能的位置编码方法。然而，它的优点是能够扩展到未知的序列长度(例如，当我们训练出的模型需要翻译远比训练集里的句子更长的句子时)。

残差模块

在继续进行下去之前，我们需要提到一个编码器架构中的细节：在每个编码器中的每个子层（自注意力、前馈网络）的周围都有一个残差连接，并且都跟随着一个“层-归一化”步骤。

层-归一化步骤：

https://arxiv.org/abs/1607.06450

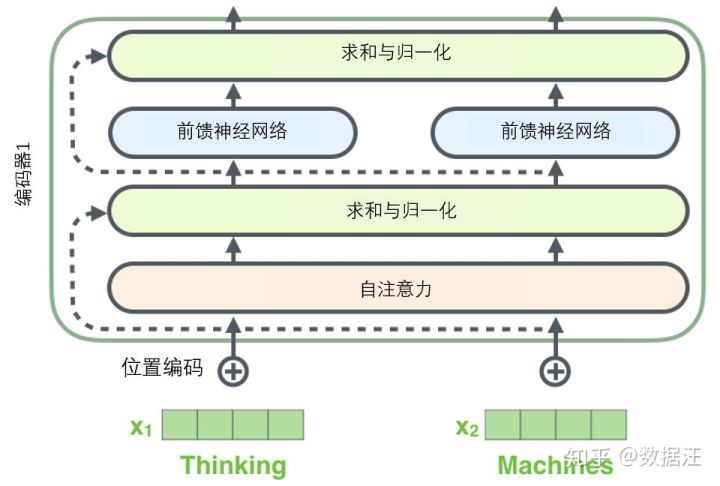
如果我们去可视化这些向量以及这个和自注意力相关联的层-归一化操作，那么看起来就像下面这张图描述一样：

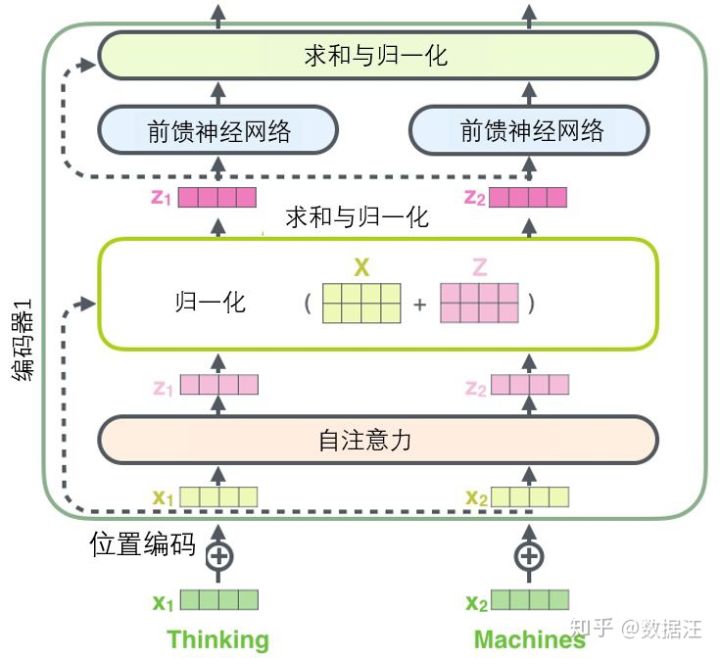
解码器的子层也是这样样的。如果我们想象一个2 层编码-解码结构的transformer，它看起来会像下面这张图一样：

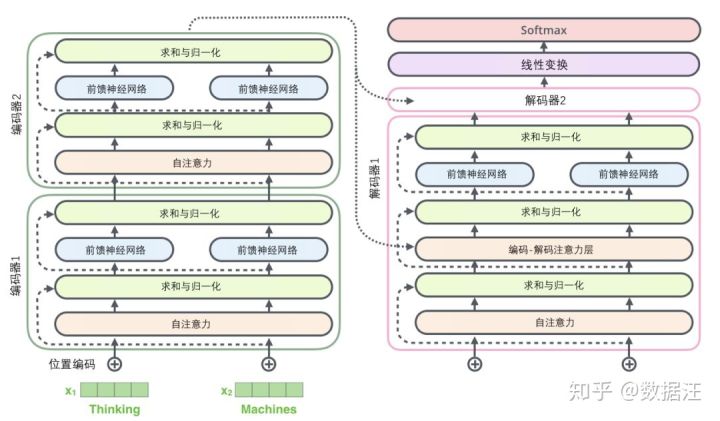
解码组件

既然我们已经谈到了大部分编码器的概念，那么我们基本上也就知道解码器是如何工作的了。但最好还是看看解码器的细节。

编码器通过处理输入序列开启工作。顶端编码器的输出之后会变转化为一个包含向量K（键向量）和V（值向量）的注意力向量集 。这些向量将被每个解码器用于自身的“编码-解码注意力层”，而这些层可以帮助解码器关注输入序列哪些位置合适：

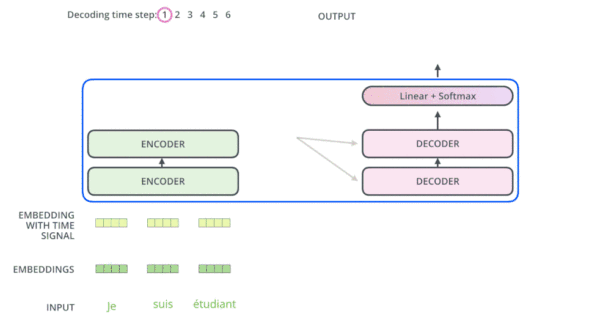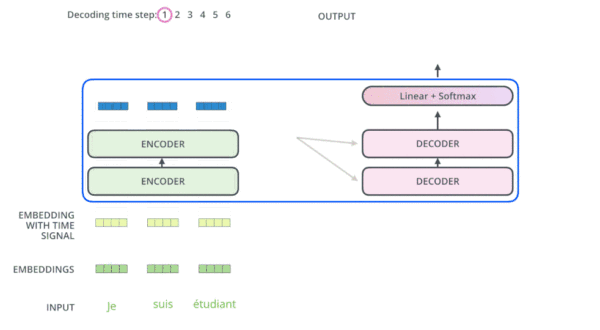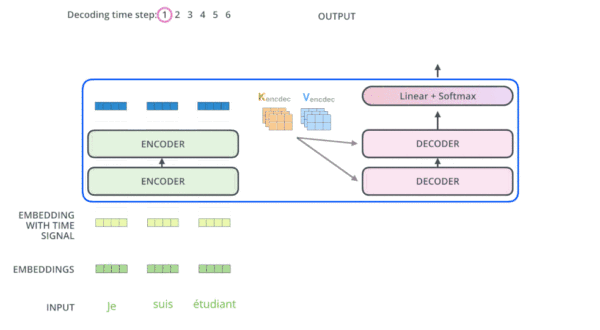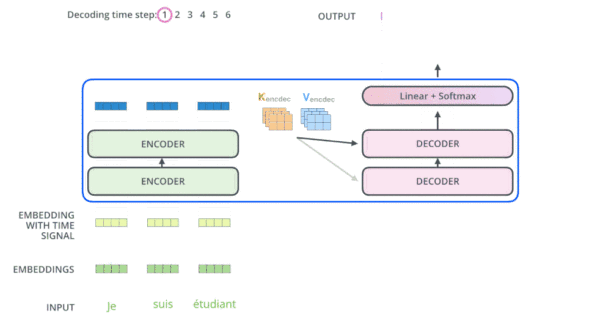
在完成编码阶段后，则开始解码阶段。解码阶段的每个步骤都会输出一个输出序列（在这个例子里，是英语翻译的句子）的元素

接下来的步骤重复了这个过程，直到到达一个特殊的终止符号，它表示transformer的解码器已经完成了它的输出。每个步骤的输出在下一个时间步被提供给底端解码器，并且就像编码器之前做的那样，这些解码器会输出它们的解码结果 。另外，就像我们对编码器的输入所做的那样，我们会嵌入并添加位置编码给那些解码器，来表示每个单词的位置。

而那些解码器中的自注意力层表现的模式与编码器不同：在解码器中，自注意力层只被允许处理输出序列中更靠前的那些位置。在softmax步骤前，它会把后面的位置给隐去（把它们设为-inf）。

这个“编码-解码注意力层”工作方式基本就像多头自注意力层一样，只不过它是通过在它下面的层来创造查询矩阵，并且从编码器的输出中取得键/值矩阵。

最终的线性变换和Softmax层

解码组件最后会输出一个实数向量。我们如何把浮点数变成一个单词？这便是线性变换层要做的工作，它之后就是Softmax层。

线性变换层是一个简单的全连接神经网络，它可以把解码组件产生的向量投射到一个比它大得多的、被称作对数几率（logits）的向量里。

不妨假设我们的模型从训练集中学习一万个不同的英语单词（我们模型的“输出词表”）。因此对数几率向量为一万个单元格长度的向量——每个单元格对应某一个单词的分数。

接下来的Softmax 层便会把那些分数变成概率（都为正数、上限1.0）。概率最高的单元格被选中，并且它对应的单词被作为这个时间步的输出。

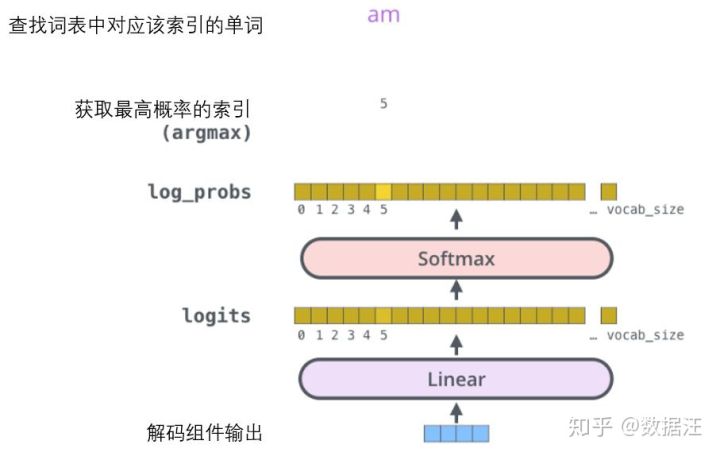
这张图片从底部以解码器组件产生的输出向量开始。之后它会转化出一个输出单词。

训练部分总结

既然我们已经过了一遍完整的transformer的前向传播过程，那我们就可以直观感受一下它的训练过程。

在训练过程中，一个未经训练的模型会通过一个完全一样的前向传播。但因为我们用有标记的训练集来训练它，所以我们可以用它的输出去与真实的输出做比较。

为了把这个流程可视化，不妨假设我们的输出词汇仅仅包含六个单词：“a”, “am”, “i”, “thanks”, “student”以及 “”（end of sentence的缩写形式）。

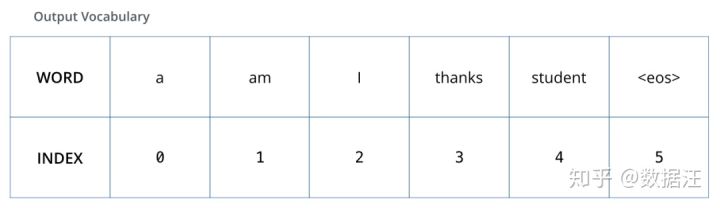
我们模型的输出词表在我们训练之前的预处理流程中就被设定好。

一旦我们定义了我们的输出词表，我们可以使用一个相同宽度的向量来表示我们词汇表中的每一个单词。这也被认为是一个one-hot 编码。所以，我们可以用下面这个向量来表示单词“am”：

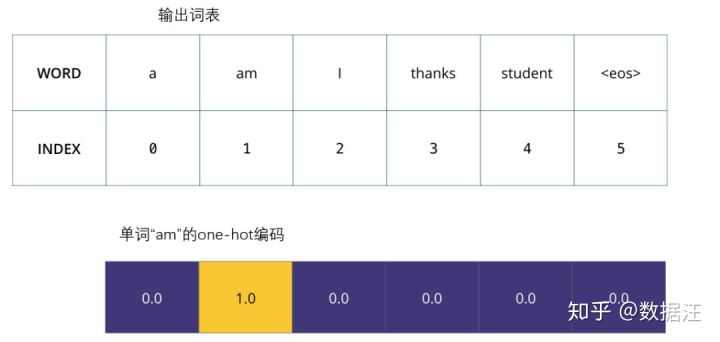
例子：对我们输出词表的one-hot 编码

接下来我们讨论模型的损失函数——这是我们用来在训练过程中优化的标准。通过它可以训练得到一个结果尽量准确的模型。

损失函数

比如说我们正在训练模型，现在是第一步，一个简单的例子——把“merci”翻译为“thanks”。

这意味着我们想要一个表示单词“thanks”概率分布的输出。但是因为这个模型还没被训练好，所以不太可能现在就出现这个结果。

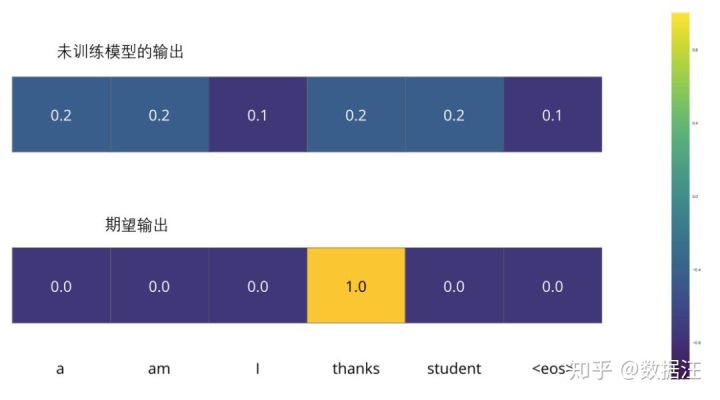
因为模型的参数（权重）都被随机的生成，（未经训练的）模型产生的概率分布在每个单元格/单词里都赋予了随机的数值。我们可以用真实的输出来比较它，然后用反向传播算法来略微调整所有模型的权重，生成更接近结果的输出。

你会如何比较两个概率分布呢？我们可以简单地用其中一个减去另一个。更多细节请参考交叉熵和KL散度。

交叉熵：

https://colah.github.io/posts/2015-09-Visual-Information/

KL散度：

https://www.countbayesie.com/blog/2017/5/9/kullback-leibler-divergence-explained

但注意到这是一个过于简化的例子。更现实的情况是处理一个句子。例如，输入“je suis étudiant”并期望输出是“i am a student”。那我们就希望我们的模型能够成功地在这些情况下输出概率分布：

  • 每个概率分布被一个以词表大小（我们的例子里是6，但现实情况通常是3000或10000）为宽度的向量所代表。
  • 第一个概率分布在与“i”关联的单元格有最高的概率
  • 第二个概率分布在与“am”关联的单元格有最高的概率
  • 以此类推，第五个输出的分布表示“”关联的单元格有最高的概率

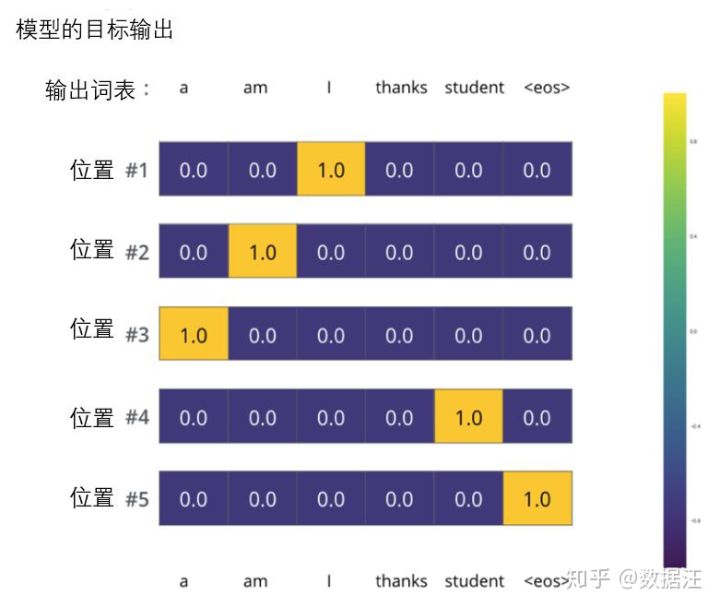
依据例子训练模型得到的目标概率分布。

在一个足够大的数据集上充分训练后，我们希望模型输出的概率分布看起来像这个样子：

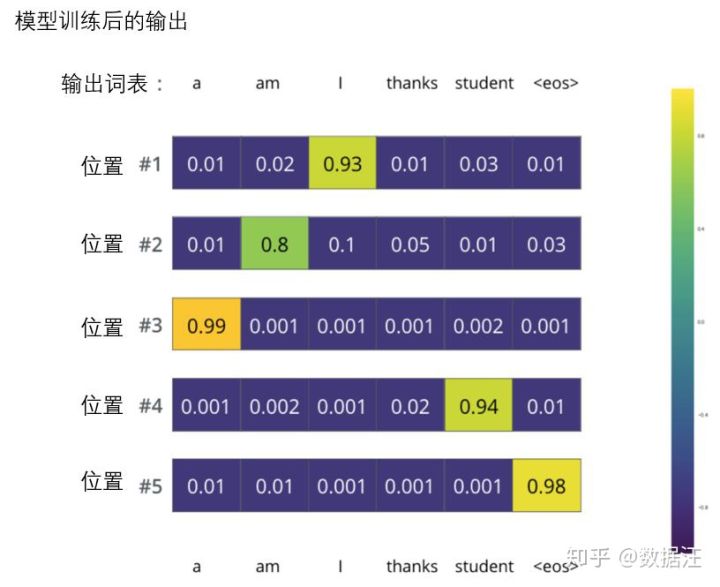
我们期望训练过后，模型会输出正确的翻译。当然如果这段话完全来自训练集，它并不是一个很好的评估指标（参考：交叉验证，链接 https://www.youtube.com/watch?v=TIgfjmp-4BA）。注意到每个位置（词）都得到了一点概率，即使它不太可能成为那个时间步的输出——这是softmax的一个很有用的性质，它可以帮助模型训练。

因为这个模型一次只产生一个输出，不妨假设这个模型只选择概率最高的单词，并把剩下的词抛弃。这是其中一种方法（叫贪心解码）。另一个完成这个任务的方法是留住概率最靠高的两个单词（例如I和a），那么在下一步里，跑模型两次：其中一次假设第一个位置输出是单词“I”，而另一次假设第一个位置输出是单词“me”，并且无论哪个版本产生更少的误差，都保留概率最高的两个翻译结果。然后我们为第二和第三个位置重复这一步骤。这个方法被称作集束搜索（beam search）。在我们的例子中，集束宽度是2（因为保留了2个集束的结果，如第一和第二个位置），并且最终也返回两个集束的结果（top_beams也是2）。这些都是可�