感知机
整理人:张辽,厦门大学信科院 计算机技术专业
weChat: zhangliaobet

主要内容
1. 补充
1.1 最小二乘法的概率解释
2. 支持向量机
2.1 模型与策略
2.2 硬间隔最大化
2.2.1 函数间隔与几何间隔
2.2.2 间隔最大化原理
2.2.3 线性可分SVM学习算法——最大间隔法
2.2.4 最大间隔法示例
2.2.5 线性可分SVM学习的对偶算法
2.2.6 对偶学习算法示例
2.3 软间隔最大化(下)
3. LR(下)

-
补充
1.1 最小二乘法的概率解释
前文向大家介绍了最小二乘的解析式以及它的几何解释,下面我们尝试从概率的角度,去探讨最小二乘与极大似然估计的关系。先做这样几个假设:
- 误差总是存在的
首先要说明的,所有的预测值都不可能完美地与真实值契合,所以误差必然存在,而我们的目的就是如何让误差尽可能地小。这样就可以假设有一组θ,使真实的数据存在以下关系式,y(i)表示真实值,θTx(i)表示预测值,ε表示误差项:
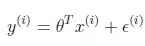
- 假设误差服从高斯分布
至于为什么可以这样假设,原因是人们认为误差是随机的,所以服从高斯分布。根据中心极限定理,也能够做出这样的假设。该定理指出,如果一个随机变量是若干独立随机变量的总和,当被加的个数趋近于无穷大时,他的概率密度函数近似高斯密度。并且误差也是独立同分布(Independent Identical Distribution,IID)。
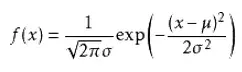
其中μ是正态分布随机变量的均值,σ2是此随机变量的方差,也可以记作N(μ,σ2)。
设ε的平均值为0,方差为ε2,ε的高斯分布,也就是ε的概率密度函数表示如下:
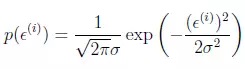
- 求真实值的概率分布
ε的概率密度函数,就是预测值与真实值差的概率密度函数,那么可以把上述两个等式合并,经过变换,得到如下等式:
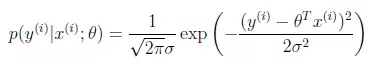
- 求联合概率分布
这样相当于给定一组θ、x,求出了y的概率密度分布,联合概率分布等于边缘概率分布的乘积:
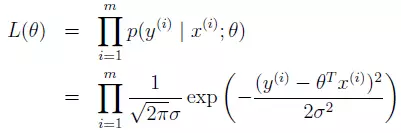
- 定义对数似然函数
这里我们就得到了一个关于x、y、θ的模型,它表示真实值y的联合概率分布。当我们想使预测正确的概率最大时,只需要将L(θ)最大化就可以了。于是,求值问题又变成了求最大值问题。为了方便计算,我们定义对数似然函数,L(θ),也就是对L(θ)取对数,再求最大值。对数函数为一个单调递增函数,所以不会对原函数造成影响。取对数后,累乘变成累加。
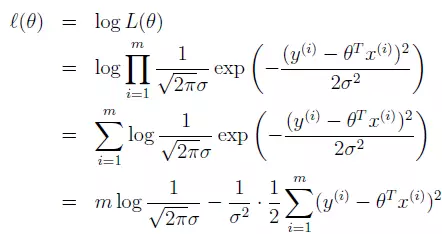
等式第一项是一个常数项,第二项是一个负数项。要让L(θ)最大,就要让负数项最小:
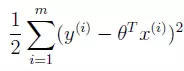
这又回到了我们熟悉的式子上面来了,简单的来说,最小二乘法就是误差服从高斯分布且独立同分布下的极大似然估计。

-
支持向量机
2.1 模型与策略
90年代的时候,在贝尔实验室,Yann Lecun和 Vapnik经常就SVM和神经网络的优劣展开激烈的讨论,但那个时候,神经网络发展的并不是很强大,反观SVM的理论研究则更加深入,通过核技巧成功将SVM的应用层面从线性可分扩展到线性不可分的情况,一度占据上风。
支持向量机(SupportVector Machine, SVM)是一种二类分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;支持向量机的学习策略是间隔最大化,可形式化为一个求解凸二次规划(convex quadratic programming)的问题,也等价于正则化的合页损失函数的最小化问题。
当训练数据可分时,通过硬间隔最大化(hardmarginmaximization),学习一个线性的分类器,即线性可分支持向量机,又称为硬间隔支持向量机;当训练数据近似可分时,通过软间隔最大化(softmargin maximization) ,也学习一个线性分类器,称为软间隔支持向量机。

** 2.2 硬间隔最大化**
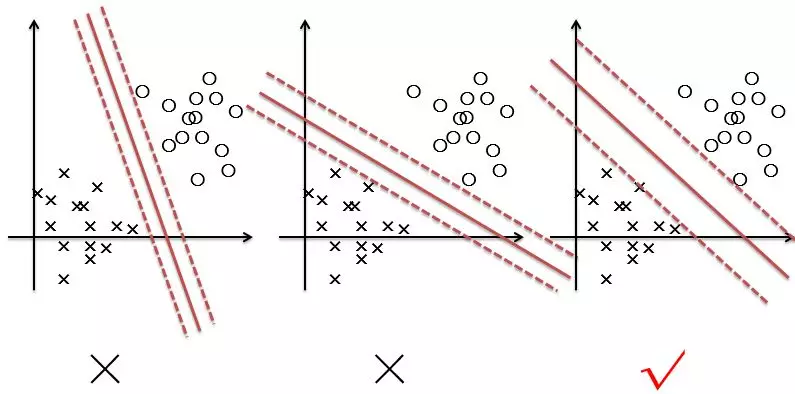
对于二维特征空间的线性可分的二分类问题,如上图所示两种类别。这时有无数个直线能将两类数据正确区分。但哪种看起来分的更 好 呢?也就是说如何去定义“好”呢,有这样两种度量方式,一种叫做 函数间隔,另外一种叫**几何间隔,**函数间隔与几何间隔的概念如下。

1.2.1 函数间隔与几何间隔
- **函数间隔 **
对于给定的训练数据集_ T 和超平面(w,b),定义超平面(w,b)关于样本点(x__i,y_i)的函数间隔为
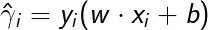
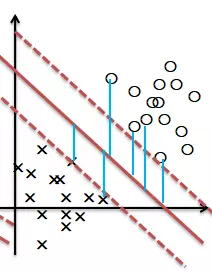
如图所示,数据点到分界面的在y轴上的距离即函数间隔(蓝线所示)。
定义超平面(w,b)关于训练数据集T的函数间隔为超平面(w,b)关于T中所有样本点(xi,yi)的函数间隔之最小值,即
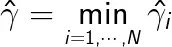
函数间隔可以表示分类预测的正确性及确信度。但是当等比例的改变w和b时,如
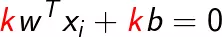
超平面没有改变,但是函数间隔变为原来的k倍,即
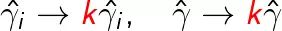
如果对超平面的法向量w加以约束,使得间隔是确定的,这时函数间隔成为几何间隔。
-
**几何间隔 **
对于给定的训练数据集T和超平面(w,b),定义超平面(w,b)关于样本点(xi,yi)的几何间隔为
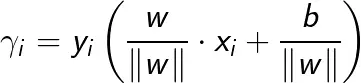
其中,||w||为 w 的L2范数。
下图为几何间隔的示例图。其中w为超平面的法向量,A点到超平面的距离为γi
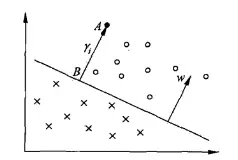
定义超平面(w,b)关于训练数据集T的几何间隔为超平面(w,b)关于T中所有样本点(xi,yi)的几何间隔之最小值,即
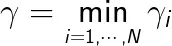
如果等比例的改变超平面参数w和b,函数间隔按比例改变,而几何间隔不变。

** 1.2.2 间隔最大化原理**
- 最大间隔分离超平面
对于一个线性可分的数据来说,我们总能找到一个超平面能将它区分开来,那么对这个超平面来说,我们也可以找到距离这个超平面最近的一些数据点,也就是与超平面几何间隔最小的这些数据点,即
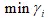 ,但是我们找的这个超平面可能不是最优的,这个最优的意思是说,不仅将这些数据正确分开,并且对于那些距离超平面最近的数据点(难分的数据点)也让它离超平面尽可能的远,这样的超平面对于未知数据就有很好的预测能力。因此我们要最大化几何间隔。也称之为硬间隔最大化。
,但是我们找的这个超平面可能不是最优的,这个最优的意思是说,不仅将这些数据正确分开,并且对于那些距离超平面最近的数据点(难分的数据点)也让它离超平面尽可能的远,这样的超平面对于未知数据就有很好的预测能力。因此我们要最大化几何间隔。也称之为硬间隔最大化。
下面我们学习如何求得最大间隔分离超平面。这个问题可以转化为下面的约束最优化问题:
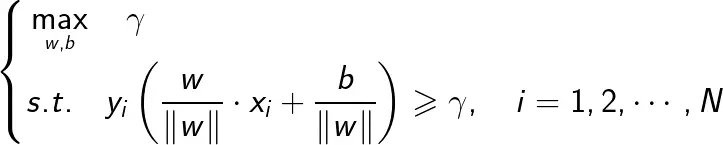
该问题第一项表示的是要求最大化超平面(w,b)关于训练集的几何间隔γ,第二项约束条件表示的是超平面(w,b)关于每个训练样本的几何间隔至少是γ。
考虑到几何间隔与函数间隔的关系,上述问题可改写为如下问题:
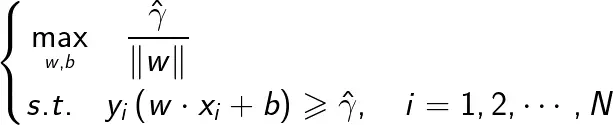
假设把w和b按照比例变为k倍,约束优化问题变为如下形式:
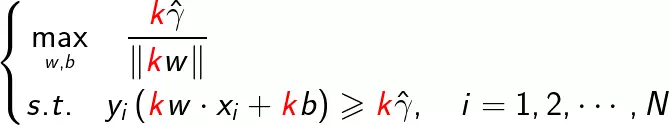
可以看出函数间隔的这一变化,对上述最优化问题的不等式约束没有影响,对目标函数的优化同样没有影响,也就是说,它产生了一个等价的最优化问题。为此取
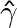 =1。另外考虑到最大化
=1。另外考虑到最大化
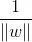 和最小化
和最小化
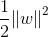 和最小是等价的。于是我们可以得到如下的线性可分支持向量机学习的最优化问题:
和最小是等价的。于是我们可以得到如下的线性可分支持向量机学习的最优化问题:
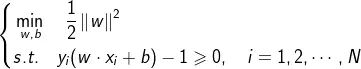

** 1.2.3 线性可分SVM学习算法——最大间隔法**
** **求解出上述约束最优化问题的解w 和b 后,那么就可以得到最大间隔分离超平面
** w** \\\*** ·x+ b \\\***** = 0**
及分类决策函数
f(x)= sign(w \\\*** ·x +b \\\*** ),
即线性可分支持向量机模型。
下面我们总结一下整个算法流程。

输入:线性可分训练数据集_ T ={(x 1 ,y 1 ),(x 2 ,y 2 ),···,(x N ,y N )} , 其中, x i ∈χ=R n ,_yi∈У={-1,+1},i= 1,2,···,N
输出:最大间隔分离超平面和分类决策函数。
- 构造并求解约束最优化问题:
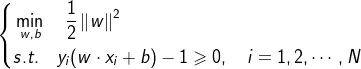
求得最优解w 和b。
-
由此得到分离超平面:
w \\\*** ·x + b \\\*** =_ _ 0
分类决策函数
f(x) = sign(w \\\*** ·x+ b \\\*** )

** 1.2.4 最大间隔法示例**
**
**
** **有如下一组数据集:
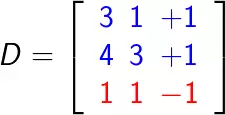
在坐标轴上如下所示:
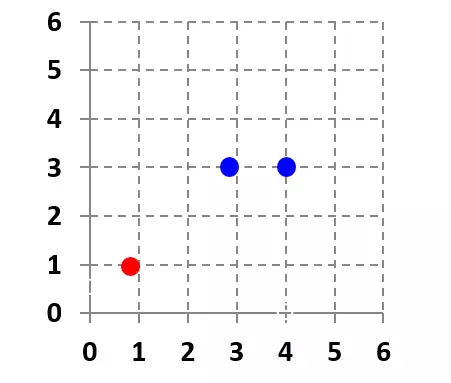
根据上述算法,根据训练数据集构造约束最优化问题:
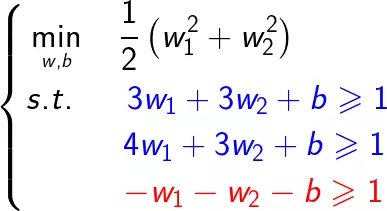
化简可得:
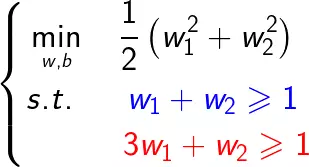
问题转化为求圆心到某一区域最小值的问题,如下图所示:
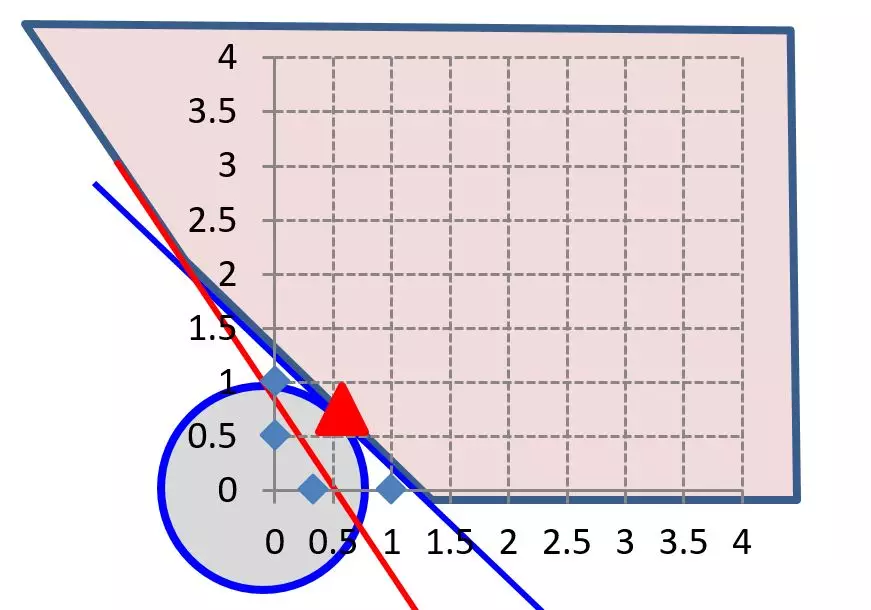
上图中红色标记所示点,即为我们要求的解。求得:
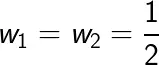
带入约束条件求b得:
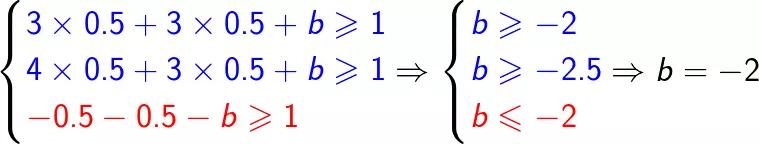
最终可得:
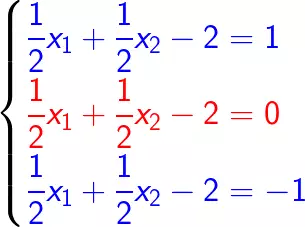
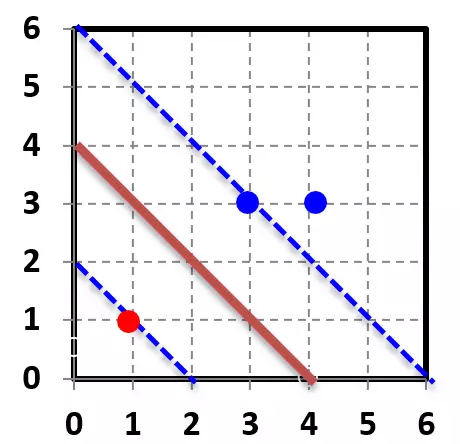
其中棕色直线是我们求得的最终分界面,而与之平行的另外两条虚线是支撑向量所在的直线,落在这两条直线上的数据点到分界面的距离相等,它们支撑起了整个分类器的分类性能,保证了最优的分类效果。

** 1.2.5 线性可分SVM学习的对偶算法**
- 拉格朗日对偶性
在约束最优化问题中,常常利用拉格朗日对偶性将原始问题转换为对偶问题,通过解对偶问题而得到原始问题的解。这样做一是因为对偶问题往往更容易求解;二是因为自然引入核函数,进而推广到非线性分类问题。
-
原始问题
考虑如下约束最优化问题
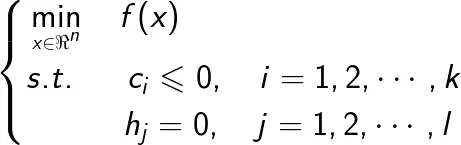
称此约束最优化问题为原始最优化问题或原始问题。
首先引入拉格朗日函数
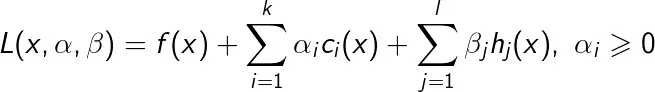
考虑x的函数
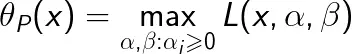
这里,下标P表示原始问题。
若存在x,使得ci(x)>0或者hj(x)≠0,则有
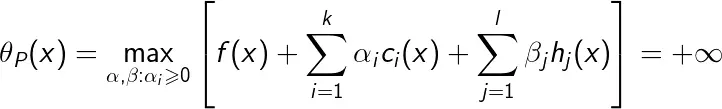
相反地,如果x满足约束条件,则
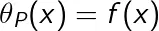
因此
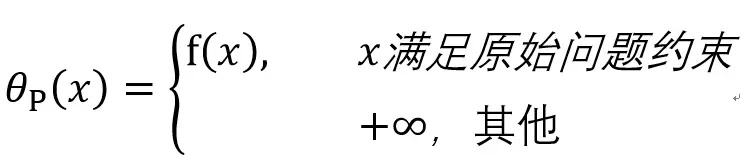
所以如果考虑极小化问题
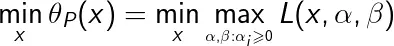
它与原始问题是等价的,即它们有相同的解。上述称为广义拉格朗日的极小极大问题。
定义原始问题的最优值
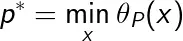
称为原始问题的值。
-
对偶问题
定义
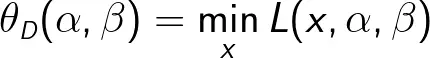
考虑极大化上述定义,即:
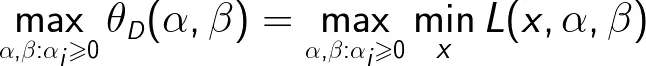
上述问题称为广义拉格朗日函数的极大极小问题。
可以把广义拉格朗日的极大极小问题表示为约束最优化问题:
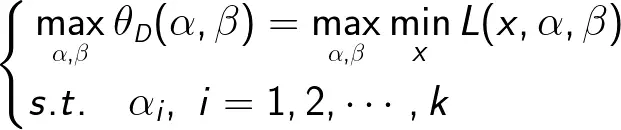
称为原始问题的对偶问题。
定义对偶问题的最优值
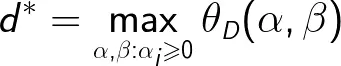
称为对偶问题的值。
-
原始问题与对偶问题的关系
对任意的α,β和x,有
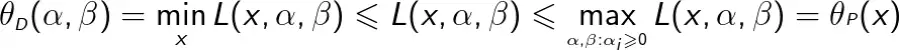
即
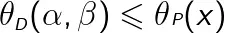
由于原始问题和对偶问题均有最优值,所以,
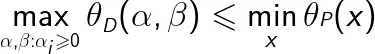
即
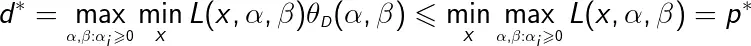
- KKT****对偶互补条件
假设函数f(x)和ci(x)是凸函数,hj(x)是仿射函数,且约束ci(x)严格可执行,则x 和α,β 分别是原始问题和对偶问题的解的充分必要条件是x 和α*,β*满足如下的KKT条件:
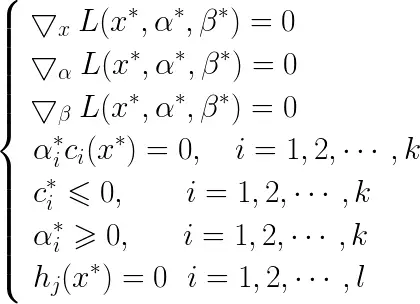
其中αi ci(x)=0称为KKT的对偶互补条件。若αi*>0,则ci(x*)=0
-
学习的对偶算法
根据拉格朗日对偶性,原始问题得对偶问题是极大极小问题:
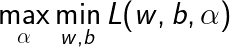
为了得到对偶问题的解,需要先求_ L(w,b,α)_对w,b的极小,再求对α的极大。
首先,定义拉格朗日函数:
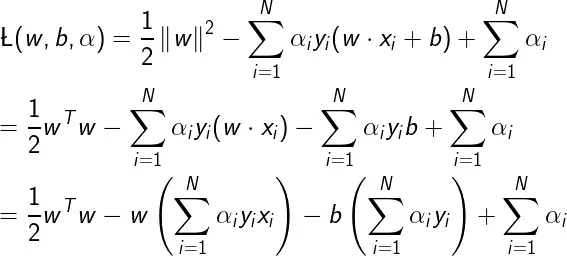
求对拉格朗日函数L(w,b,α)分别求偏导并令其为0得:
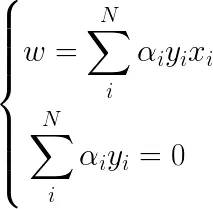
把求导所得带入拉格朗日函数:
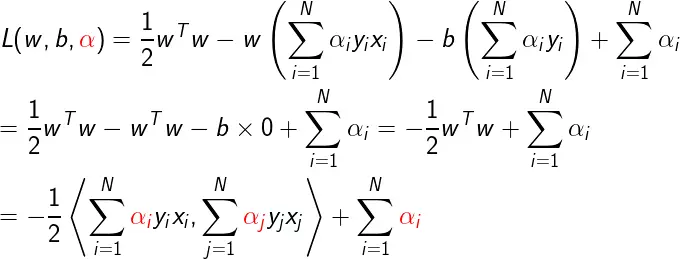
即
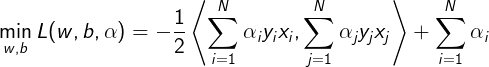
接下来再求对α的极大,即是对偶问题:
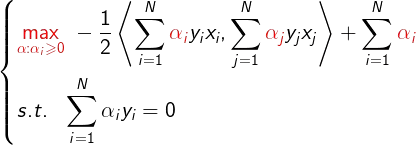
将该问题的目标函数由求极大转为求极小,得到与之等价的对偶最优化问题:
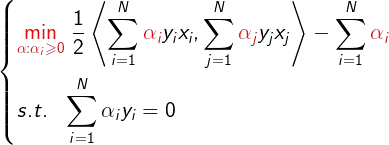
把目标函数展开成如下形式:
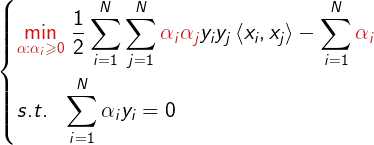
设
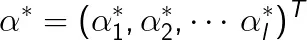 是上述对偶最优化问题的解,设原始最优化问题的解w 和b。我们接下�
是上述对偶最优化问题的解,设原始最优化问题的解w 和b。我们接下�
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/%E4%BA%92%E8%81%94%E7%BD%91/%E6%84%9F%E7%9F%A5%E6%9C%BA/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


