张俊林

导读: 推荐或者 CTR 预估任务有一个很突出的特点：存在海量稀疏特征。海量意味着数量巨大，稀疏意味着即使在很大的训练数据里，大量特征出现频次也非常低，这往往是由于引入了大量 ID 类特征带来的。对于 DNN 排序系统，是否能够找到好的特征 Embedding 表达方式，对于系统效果是至关重要的。

虽然说，如何更好地表征稀疏特征对于模型的泛化能力至关重要，但是，关于这块的研究，除了经典的特征 Onehot 到稠密 Embedding 映射模式外，之前并未太受到重视，最近一年开始逐步涌现出一些相关工作。对于序列行为中的 Item Embedding，拥有怎样性质的 Embedding 表达方式是较好的？对于非行为序列的推荐模型，关于特征 Embedding，大家常规采用的做法是：将特征的 Embedding Size 作为超参，通过手工测试来寻找好的 Embedding 大小。然而，是否有更好的方式？这些都是悬而未决的问题。

本文将介绍两个与稀疏特征 Embedding 相关的工作，一篇来自于阿里妈妈发表在 DLP-KDD2019 的论文，回答了第一个问题（DLP-KDD2020 研讨会集中探讨大规模稀疏条件下可落地的推荐广告等技术方案，目前正在征集稿件过程中，欢迎赐稿。对，这里是广告，如果太精简，看广告不过瘾的话，文末还有）；另外一篇来自于谷歌，尝试解决第二个问题。

用户行为序列中的 Item Embedding

用户行为是推荐系统中很有价值的可利用信息，一般我们可以用户实施过行为的一系列物品作为某个用户兴趣的表征，通常采用遵循时间序的 Item ID 队列作为行为序列的输入。由于工业界应用物品数量巨大，所以大多数 Item 是稀疏的。而我们关心的一个问题是：对于用户行为序列中的 Item ID 来说，拥有什么性质的 Embedding 表达方式是好的？Res-embedding for Deep Learning Based Click-Through Rate Prediction Modeling 回答了这个问题。

Res-embedding 首先在理论上证明了：神经网络 CTR 模型的泛化误差与 Item 在 Embedding 空间的分布密切相关，如果用户兴趣相近的各 Item，在 Embedding 空间中的 envelope 半径越小，也就是说，相同兴趣 Item 之间在 embedding 空间中越紧致，形成的簇半径越小，则模型泛化误差越小，也就是模型的泛化能力越好。这个结论是很有意义的。因为可以用这一结论，在训练过程中约束 Item Embedding，让其满足一定条件，以此来增加模型能力。在此结论基础上，Res-embedding 提出了一个较为通用的方法：对于相近用户兴趣的 Item Embedding，我们让它由两部分叠加构成，一个是属于这个兴趣内的所有 Item 共享的兴趣中心 Central Embedding，另外一个是 Item 自身的残差 Residual Embedding:

    Item Embedding=Central Embedding + Residual embedding

因为 Central Embedding 共享，是相同的，那么只要约束残差 Residual Embedding 的数值变动范围能在一个较小的范围内，自然就能保证达成上述目标，以此来泛化模型性能。下图比较形象地展示了这一做法：

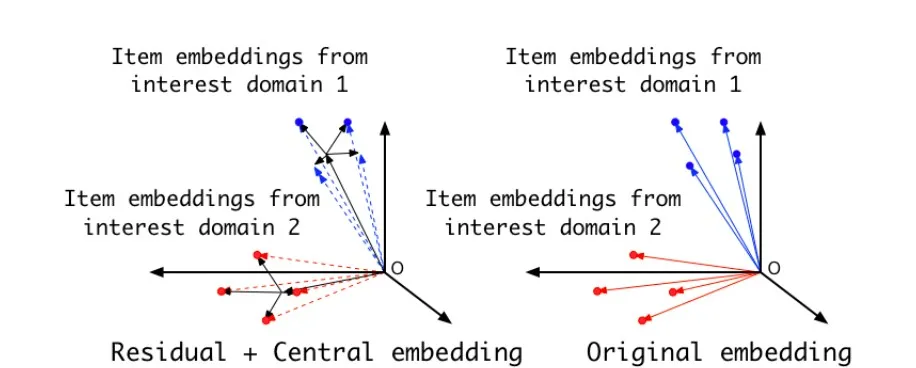
由图中可看出，如果采取这种约束方式，与不做约束相比，可以保证相近兴趣 Item Embedding 形成的类簇具备较小的半径，由此增加模型泛化性能。

但是，我们无法事先获知某个 Item 隶属于哪个用户兴趣，如何获得 Item 与簇中心 Central Embedding 的隶属关系呢？Res-embedding 提出在用户共访 Item 图上的三种具体方法，包括一种 GNN 的方法，这里不展开讲了，感兴趣的同学可以参考原文。

非行为序列类推荐任务中的特征 Embedding

对于 CTR 任务来说，存在海量稀疏特征，导致 DNN 排序模型中绝大多数参数是由特征 Embedding 构成的。那么，如何更有效地优化特征 Embedding 表达对于模型能力就至关重要。

我们先设想一个比较完美的特征 Embedding 分配方案，如果它存在，应该是这个样子的：对于高频出现的特征，能够分配给它较长的 Embedding 大小，使其能更充分地编码和表达信息。而对于低频的特征，则希望分配较短的 Embedding，因为对于低频特征，它在训练数据中出现次数少，如果分配了较长的 Embedding，更容易出现过拟合现象，影响模型泛化性能。而对于那些极低频的特征，基本学不了什么知识，反而会带来各种噪音，那么我们可以不分配或者让它们共享一个公有 Embedding 即可。

上面说的设想，只是一个期望，那么具体怎么做才能达到这点呢？谷歌在 Neural Input Search for Large Scale Recommendation Models（NIS）文中提出用强化学习来实施这一目标。具体而言，不同的 Embedding 分配方案，形成了搜索空间，它使用 ENAS 来在搜索空间中找到最佳的 Embedding 分配方案。细节不表，只说思路，下图展示的例子基本能够说明问题：

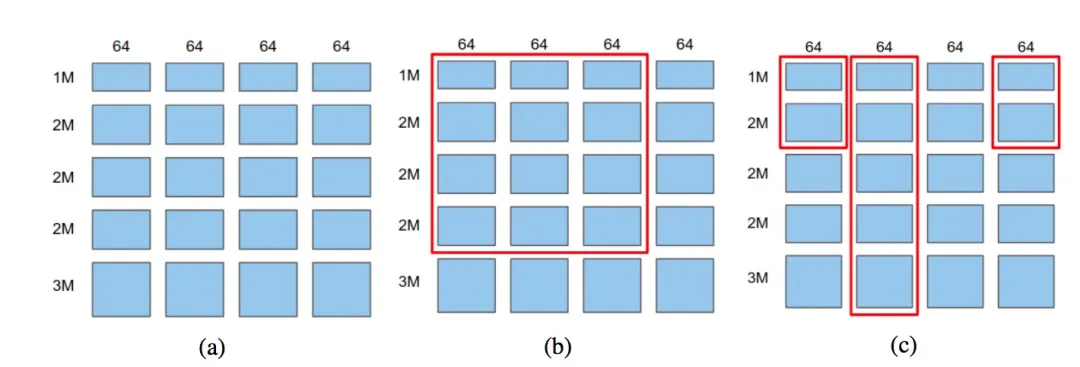
常规的特征 Embedding，一般是给所有特征一个固定大小的 Embedding Size，而为了能够更灵活地表达不同的 Embedding 分配方案，NIS 把特征 Embedding 二维空间切割成 Block，如图中 (a) 所示，纵坐标是特征维度，比如共有 10 Million 个特征，则划成 1M/2M/2M/2M/3M 几段，而横坐标则是 Embedding Size 维度，最长允许 256 bit，按照 64 bit 为单位，划分成 4 段。这样就形成了 Embedding 的二维 Block 结构，不同的 Block 组成，就构成了不同的 Embedding 分配方案。

常规的 Embedding 方案，一般 Embedding Size 是个超参，需要手工去尝试，而 NIS 也可以提供最佳 Embedding Size 的搜索，就是图中 (b) 所示，从左上角作为起点，划出各种红色矩形框，不同大小的矩形框就是不同的分配方案。纵坐标里红框外的特征共享同一个 Embedding，等价于没有给它分配，而分配了 Embedding 的所有特征，Embedding Size 是相同大小的。所以对于这种情况，ENAS 的决策点在于：哪些特征值得分配空间，以及最优的 Embedding Size 应该是多大。

尽管这样能够代替手工试探 Embedding Size，但是仍未能达成完美 Embedding 分配方案的需求，我们还希望高频有效特征，能够分配更长的 Embedding Size，而信息含量比较少的特征，则只分配较少 Embedding Size 甚至不分配。在这个 Block 框架下，如何达成这一点呢，参考图中 (c) 图，我们只需要在 b 的基础上，在列也就是 Embedding Size 维度，进行多步决策即可，首先对于第一列 64 Bit，划出一个矩形框，代表 1M+2M 的那些特征，分配了 64bit 的 Embedding 空间，每一列依次这样做决策，即可实现不同特征分配不同长度的目的。比如图中所示，进行了 4 步决策后，1M+2M 的特征，分配了 64*3 个 bit 的 Embedding Size，而剩余的特征，则分配了 64bit 的 Embedding Size。如此这般，即可实现我们希望达成的目标。

我们可以分析下，图中 (c) 方案的决策或者搜索空间有多大，很明显每一步有 5 种选择，有 4 个决策步骤，所以决策空间大小为 5 的 4 次方，就是说有这么多种分配方案，而 ENAS 通过某个分配方案在验证集数据下的 AUC 评价指标表现，以及方案耗费 Embedding 空间大小，来评估每个决策方案的优劣程度。我们肯定是鼓励验证集合指标表现好，耗费空间少的方案，而强化学习的 Reward 就是这个思路来设计的。通过这种模式，即可设计强化学习方案来寻找出最优的 Embedding 方案。而试验结果也说明了通过这种方