推荐系统系列二算法理论与实践
背景
在 CTR/CVR 预估任务中,除了 FM 模型[2] 之外,后起之秀 FFM(Field-aware Factorization Machine)模型同样表现亮眼。FFM 可以看作是 FM 的升级版,Yuchi Juan 于 2016 年提出该模型,但其诞生是受启于 Rendle 在 2010 年发表的另一个模型 PITF [3](FM 也是 Rendle 在 2010 年发表的),其论文原文 [1] 中写道:
The idea of FFM originates from PITF proposed for recommender systems with personalized tags.
在各种深度推荐模型出来之前,FM/FFM 模型在各大推荐相关的竞赛中大放异彩。今天,我们就来好好梳理一下 FFM 的原理以及如何将理论转化为实践。
分析
1. FFM 公式定义
相较于 FM 模型,FFM 模型引入了域(Field)的概念(该想法来源于 PITF [3]),可看做是对特征进行分组。例如,对于性别特征而言,通常有两种取值






FFM 公式化定义如下:

其中



将公式(1)对比 FM 可以发现,二者之间的差异仅在于二阶交叉对应的隐向量。设数据集中 Field 的数目为





2. 求解
由于引入了 Field,公式(1)不能像 FM 那样进行改写,所以 FFM 模型进行 推断 时的时间复杂度为

为了方便推导各参数的梯度,隐向量表示为


当参数为


当参数为


当参数为



3. 性能评估
上述小节并未得到统一的参数梯度表达式,但估计模型训练时的时间复杂度,仍需评估更新






有,

所以,更新参数




2.



有,

所以,更新参数




综上,更新二阶项参数所需时间复杂度为





总结:FFM 训练/推断 时间复杂度都为

4. 优缺点
优点:
- 在高维稀疏性数据集中表现很好。
- 相对 FM 模型精度更高,特征刻画更精细。
缺点:
- 时间开销大。FFM 时间复杂度为
,FM 时间复杂度为
。
- 参数多容易过拟合,必须设置正则化方法,以及早停的训练策略。
5. 注意事项
FFM 对于数据集的要求 [1]:
- FFMs should be effective for data sets that contain categorical features and are transformed to binary features.
- If the transformed set is not sparse enough, FFMs seem to bring less benefit.
- It is more difficult to apply FFMs on numerical data sets.
- 含有类别特征的数据集,且需要对特征进行二值化处理。
- 越是稀疏的数据集表现效果相较于其他模型更优。
- FFM 比较难应用于纯数值类型的数据集。
数据预处理 [4]:
与 FM 一样,最好先进行特征归一化,再进行样本归一化。
超参数对于模型的影响 [1]:
首先需要注意的是,FFM 的隐向量维度远小于 FM 的隐向量维度,即

- 隐向量维度
对于模型的影响不大。
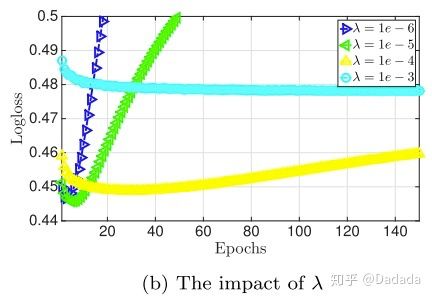
 2)正则化系数
2)正则化系数

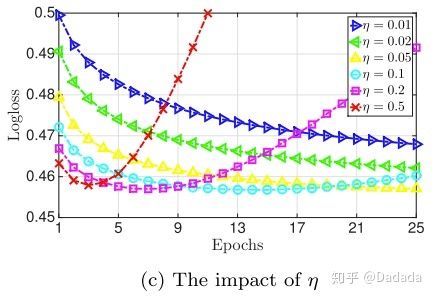
 3)在论文中,使用的是 Adagrad 优化器,全局学习率
3)在论文中,使用的是 Adagrad 优化器,全局学习率


 模型训练加速 [1,4]:
模型训练加速 [1,4]:
- 梯度分布计算;2)自适应学习率;3)多核并行计算;4)SSE3 指令并行编程;
实验
与 FM 一致使用



论文中使用的
将样本构造为-1、1 的二分类,同时使用的是
优化算法 [1]
核心代码如下:
|
|
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/%E4%BA%92%E8%81%94%E7%BD%91/%E6%8E%A8%E8%8D%90%E7%B3%BB%E7%BB%9F%E7%B3%BB%E5%88%97%E4%BA%8C%E7%AE%97%E6%B3%95%E7%90%86%E8%AE%BA%E4%B8%8E%E5%AE%9E%E8%B7%B5/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


