推荐系统遇上深度学习十一神经协同过滤原理及实战
作者: 石晓文,中国人民大学信息学院在读研究生
个人公众号:小小挖掘机(ID:wAIsjwj)
好久没更新该系列了,最近看到了一篇关于神经协同过滤的论文,感觉还不错,跟大家分享下。
论文地址: https://www.comp.nus.edu.sg/~xiangnan/papers/ncf.pdf
1、Neural Collaborative Filtering
1.1 背景
本文讨论的主要是隐性反馈协同过滤解决方案,先来明确两个概念:显性反馈和隐性反馈:
显性反馈 行为包括用户明确表示对物品喜好的行为
隐性反馈 行为指的是那些不能明确反应用户喜好
举例来说:

很多应用场景,并没有显性反馈的存在。因为大部分用户是沉默的用户,并不会明确给系统反馈“我对这个物品的偏好值是多少”。因此,推荐系统可以根据大量的隐性反馈来推断用户的偏好值。
根据已得到的隐性反馈数据,我们将用户-条目交互矩阵Y定义为:

但是,Yui为1仅代表二者有交互记录,并不代表用户u真的喜欢项目i,同理,u和i没有交互记录也不能代表u不喜欢i。这对隐性反馈的学习提出了挑战,因为它提供了关于用户偏好的噪声信号。虽然观察到的条目至少反映了用户对项目的兴趣,但是未查看的条目可能只是丢失数据,并且这其中存在自然稀疏的负反馈。
在隐性反馈上的推荐问题可以表达为估算矩阵 Y中未观察到的条目的分数问题(这个分数被用来评估项目的排名)。形式上它可以被抽象为学习函数:
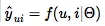
为了处理缺失数据,有两种常见的做法:要么将所有未观察到的条目视作负反馈,要么从没有观察到条目中抽样作为负反馈实例。
1.2 矩阵分解及其缺陷
传统的求解方法是矩阵分解(MF,Matrix Factorization),为每个user和item找到一个隐向量,问题变为:
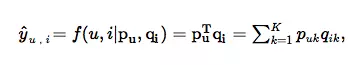
这里的 K表示隐式空间(latent space)的维度。正如我们所看到的,MF模型是用户和项目的潜在因素的双向互动,它假设潜在空间的每一维都是相互独立的并且用相同的权重将它们线性结合。因此,MF可视为隐向量(latent factor)的线性模型。
论文中给出了一个例子来说明这种算法的局限性:

1(a)是user-item交互矩阵,1(b)是用户的隐式空间,论文中强调了两点来理解这张图片:
1)MF将user和item分布到同样的隐式空间中,那么两个用户之间的相似性也可以用二者在隐式空间中的向量夹角来确定。
2)使用Jaccard系数来作为真实的用户相似性。
通过MF计算的相似性与Jaccard系数计算的相似性也可以用来评判MF的性能。我们先来看看Jaccard系数


上面的示例显示了MF因为使用一个简单的和固定的内积,来估计在低维潜在空间中用户-项目的复杂交互,从而所可能造成的限制。解决该问题的方法之一是使用大量的潜在因子 K (就是隐式空间向量的维度)。然而这可能对模型的泛化能力产生不利的影响(e.g. 数据的过拟合问题),特别是在稀疏的集合上。论文通过使用DNNs从数据中学习交互函数,突破了这个限制。
1.3 NCF
本文先提出了一种通用框架:
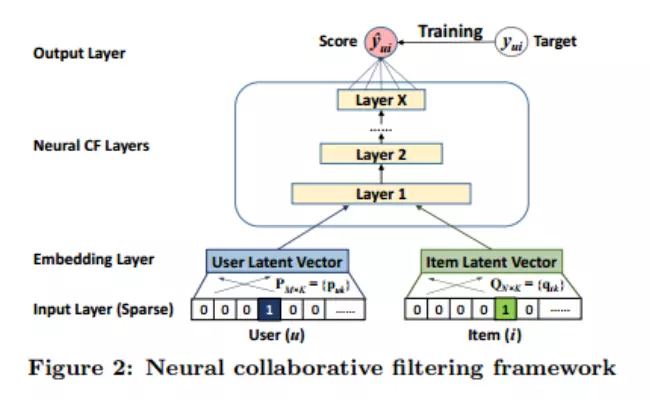
针对这个通用框架,论文提出了三种不同的实现,三种实现可以用一张图来说明:
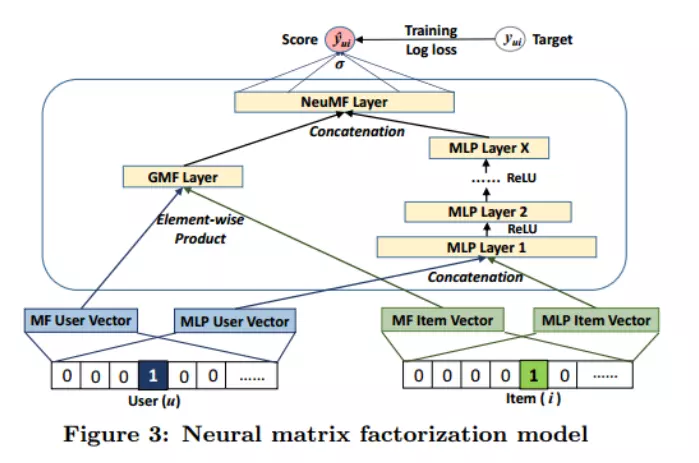
GMF:
上图中仅使用GMF layer,就得到了第一种实现方式GMF,GMF被称为广义矩阵分解,输出层的计算公式为:
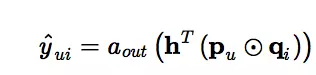
MLP
上图中仅使用右侧的MLP Layers,就得到了第二种学习方式,通过多层神经网络来学习user和item的隐向量。这样,输出层的计算公式为:
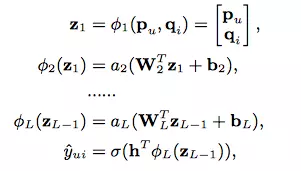
NeuMF
结合GMF和MLP,得到的就是第三种实现方式,上图是该方式的完整实现,输出层的计算公式为:
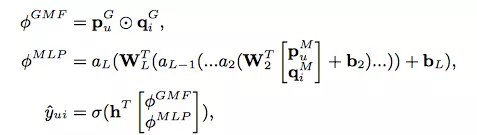
1.4 模型实验
论文通过三个角度进行了试验:
RQ1 我们提出的NCF方法是否胜过 state-of-the-art 的隐性协同过滤方法?
RQ2 我们提出的优化框架(消极样本抽样的logloss)怎样为推荐任务服务?
RQ3 更深的隐藏单元是不是有助于对用户项目交互数据的学习?
使用的数据集:MovieLens 和 Pinterest 两个数据集
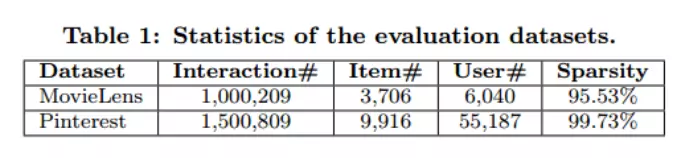
评估方案:为了评价项目推荐的性能,论文采用了leave-one-out方法评估,即:对于每个用户,我们将其 最近的一次交互作为测试集(数据集一般都有时间戳),并利用余下的培训作为训练集。由于在评估过程中为每个用户排列所有项目花费的时间太多,所以遵循一般的策略,随机抽取100个不与用户进行交互的项目,将测试项目排列在这100个项目中。排名列表的性能由**命中率(HR) 和 归一化折扣累积增益(NDCG)**来衡量。同时,论文将这两个指标的排名列表截断为10。如此一来,HR直观地衡量测试项目是否存在于前10名列表中,而NDCG通过将较高分数指定为顶级排名来计算命中的位置。本文计算每个测试用户的这两个指标,并求取了平均分。
Baselines,论文将NCF方法与下列方法进行了比较:ItemPop,ItemKNN,BPR,eALS。
以下是三个结果的贴图,关于试验结果的解读,由于篇幅的原因,大家可以查看原论文。
RQ1试验结果
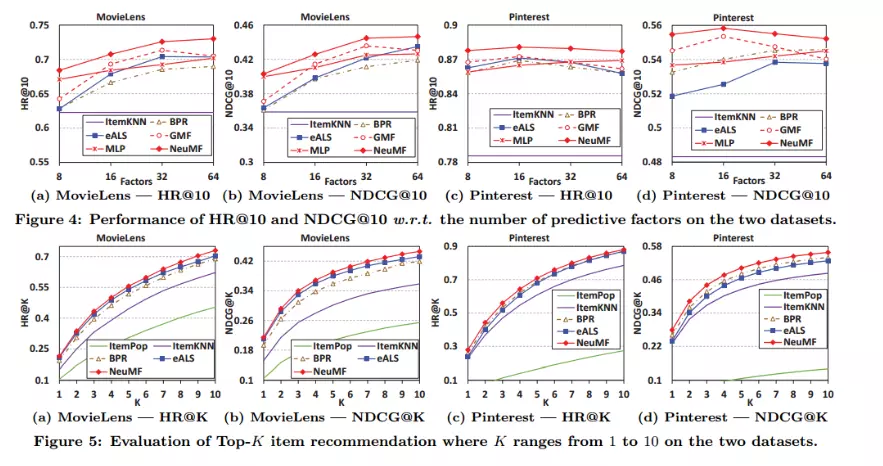
简单的结论,即NCF效果好于BaseLine模型,如果不好的话论文也不用写了,哈哈。
RQ2试验结果
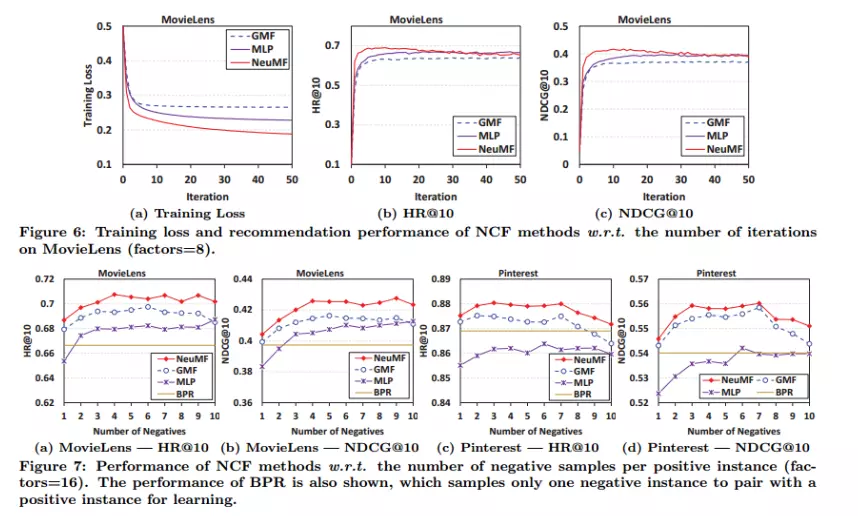
Figure 6 表示将模型看作一个二分类任务并使用logloss作为损失函数时的训练效果。
Figure7 表示采样率对模型性能的影响(横轴是采样率,即负样本与正样本的比例)。
RQ3试验结果
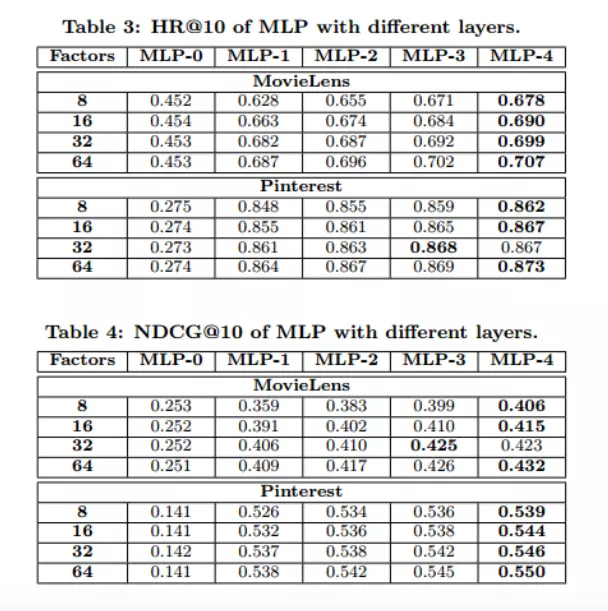
上面的表格设置了两个变量,分别是Embedding的长度K和神经网络的层数,使用类似网格搜索的方式展示了在两个数据集上的结果。增加Embedding的长度和神经网络的层数是可以提升训练效果的。
2、NCF实战
本文的github地址为: https://github.com/princewen/tensorflow_practice/tree/master/recommendation/Basic-NCF-Demo
本文仅介绍模型相关细节,数据处理部分就不介绍啦。
项目结构如下:
数据输入
本文使用了一种新的数据处理方式,不过我们的输入就是三个:userid,itemid以及label,对训练集来说,label是0-1值,对测试集来说,是具体的itemid
def get_data(self):
sample = self.iterator.get_next()
self.user = sample['user']
self.item = sample['item']
self.label = tf.cast(sample['label'],tf.float32)
定义初始化方式、损失函数、优化器
def inference(self):
""" Initialize important settings """
self.regularizer = tf.contrib.layers.l2_regularizer(self.regularizer_rate)
if self.initializer == 'Normal':
self.initializer = tf.truncated_normal_initializer(stddev=0.01)
elif self.initializer == 'Xavier_Normal':
self.initializer = tf.contrib.layers.xavier_initializer()
else:
self.initializer = tf.glorot_uniform_initializer()
if self.activation_func == 'ReLU':
self.activation_func = tf.nn.relu
elif self.activation_func == 'Leaky_ReLU':
self.activation_func = tf.nn.leaky_relu
elif self.activation_func == 'ELU':
self.activation_func = tf.nn.elu
if self.loss_func == 'cross_entropy':
# self.loss_func = lambda labels, logits: -tf.reduce_sum(
# (labels * tf.log(logits) + (
# tf.ones_like(labels, dtype=tf.float32) - labels) *
# tf.log(tf.ones_like(logits, dtype=tf.float32) - logits)), 1)
self.loss_func = tf.nn.sigmoid_cross_entropy_with_logits
if self.optim == 'SGD':
self.optim = tf.train.GradientDescentOptimizer(self.lr,
name='SGD')
elif self.optim == 'RMSProp':
self.optim = tf.train.RMSPropOptimizer(self.lr, decay=0.9,
momentum=0.0, name='RMSProp')
elif self.optim == 'Adam':
self.optim = tf.train.AdamOptimizer(self.lr, name='Adam')
得到embedding值
分别得到GMF和MLP的embedding向量,当然也可以使用embedding_lookup方法:
with tf.name_scope('input'):
self.user_onehot = tf.one_hot(self.user,self.user_size,name='user_onehot')
self.item_onehot = tf.one_hot(self.item,self.item_size,name='item_onehot')
with tf.name_scope('embed'):
self.user_embed_GMF = tf.layers.dense(inputs = self.user_onehot,
units = self.embed_size,
activation = self.activation_func,
kernel_initializer=self.initializer,
kernel_regularizer=self.regularizer,
name='user_embed_GMF')
self.item_embed_GMF = tf.layers.dense(inputs=self.item_onehot,
units=self.embed_size,
activation=self.activation_func,
kernel_initializer=self.initializer,
kernel_regularizer=self.regularizer,
name='item_embed_GMF')
self.user_embed_MLP = tf.layers.dense(inputs=self.user_onehot,
units=self.embed_size,
activation=self.activation_func,
kernel_initializer=self.initializer,
kernel_regularizer=self.regularizer,
name='user_embed_MLP')
self.item_embed_MLP = tf.layers.dense(inputs=self.item_onehot,
units=self.embed_size,
activation=self.activation_func,
kernel_initializer=self.initializer,
kernel_regularizer=self.regularizer,
name='item_embed_MLP')
GMF
GMF部分就是求两个embedding的内积:
with tf.name_scope("GMF"):
self.GMF = tf.multiply(self.user_embed_GMF,self.item_embed_GMF,name='GMF')
MLP
with tf.name_scope("MLP"):
self.interaction = tf.concat([self.user_embed_MLP, self.item_embed_MLP],
axis=-1, name='interaction')
self.layer1_MLP = tf.layers.dense(inputs=self.interaction,
units=self.embed_size * 2,
activation=self.activation_func,
kernel_initializer=self.initializer,
kernel_regularizer=self.regularizer,
name='layer1_MLP')
self.layer1_MLP = tf.layers.dropout(self.layer1_MLP, rate=self.dropout)
self.layer2_MLP = tf.layers.dens
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/%E4%BA%92%E8%81%94%E7%BD%91/%E6%8E%A8%E8%8D%90%E7%B3%BB%E7%BB%9F%E9%81%87%E4%B8%8A%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0%E5%8D%81%E4%B8%80%E7%A5%9E%E7%BB%8F%E5%8D%8F%E5%90%8C%E8%BF%87%E6%BB%A4%E5%8E%9F%E7%90%86%E5%8F%8A%E5%AE%9E%E6%88%98/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


