推荐系统遇上深度学习十三方法浅析及实现
作者:石晓文的学习日记
链接: https://www.jianshu.com/p/e0e843d78e3c
上一篇中介绍了Bandit算法,并介绍了几种简单的实现,如 Epsilon-Greedy算法,Thompson sampling算法和UCB算法。
但是传统的实现方法存在很大的缺陷,主要是缺乏用附加信息刻画决策过程的机制。今天的文章就来介绍一种结合上下文信息的Bandit方法,LinUCB,它是Contextual bandits算法框架的一种。
本文的原文是雅虎的新闻推荐算法: https://arxiv.org/pdf/1003.0146.pdf。里面公式是真的挺多的,而且涉及到了两种linUCB算法,本文只介绍第一种方法。感兴趣的同学可以阅读原文。
LinUCB浅析
这里只简单介绍一下LinUCB算法的流程,真的是浅析,浅析!
在推荐系统中,通常把待推荐的商品作为MAB问题的arm。UCB是context-free类的算法,没有充分利用推荐场景的上下文信息,为所有用户的选择展现商品的策略都是相同的,忽略了用户作为一个个活生生的个性本身的兴趣点、偏好、购买力等因素,因而,同一个商品在不同的用户、不同的情景下接受程度是不同的。故在实际的推荐系统中,context-free的MAB算法基本都不会被采用。
与context-free MAB算法对应的是Contextual Bandit算法,顾名思义,这类算法在实现E&E时考虑了上下文信息,因而更加适合实际的个性化推荐场景。
在LinUCB中,每一个arm维护一组参数,用户和每一个arm的组合可以形成一个上下文特征(上下文特征的特征维度为d),那么对于一个用户来说,在每个arm上所能够获得的期望收益如下:
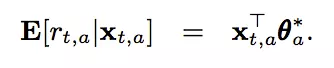
对于一个老虎机来说,假设收集到了m次反馈,特征向量可以写作Da(维度为m_d),假设我们收到的反馈为Ca(维度为m_1),那么通过求解下面的loss,我们可以得到当前每个老虎机的参数的最优解:
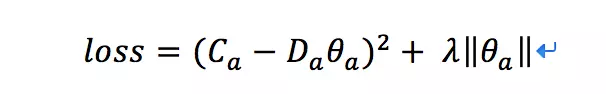
这其实就是岭回归嘛,我们很容易得到最优解为:
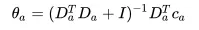
既然是UCB方法的扩展,我们除了得到期望值外,我们还需要一个置信上界,但是,我们没法继续用Chernoff-Hoeffding Bound的定理来量化这个上界,幸运的是,这个上界已经被人找到了:
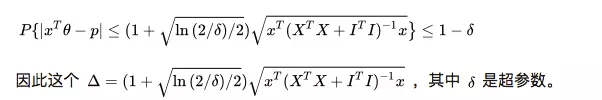
因此,我们推荐的item就能够确定了:
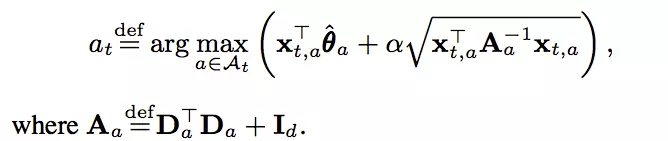
可以看到,我们在计算参数及最后推荐结果的时候,用到了以下几部分的信息:上下文特征x,用户的反馈c。而这些信息都是可以每次都存储下来的,因此在收集到了一定的信息之后,参数都可以动态更新,因此我们说LinUCB是一种 在线学习方法。
什么是在线学习?个人简单的理解就是模型的训练和更新是在线进行的,能够实时的根据在线上的反馈更新模型的参数。
好了,我们来看一下linUCB算法的流程吧:

上面的ba可以理解为特征向量x和反馈r的乘积。
是否觉得一头雾水,不用着急,我们通过代码来一步步解析上面的流程。
2、linUCB代码实战
本文的代
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/%E4%BA%92%E8%81%94%E7%BD%91/%E6%8E%A8%E8%8D%90%E7%B3%BB%E7%BB%9F%E9%81%87%E4%B8%8A%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0%E5%8D%81%E4%B8%89%E6%96%B9%E6%B3%95%E6%B5%85%E6%9E%90%E5%8F%8A%E5%AE%9E%E7%8E%B0/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


