作者&编辑 | 言有三

公众号： 有三 AI

模型剪枝作为一项历史悠久的模型压缩技术，当前已经有了比较大的进步和发展，本文给大家梳理模型剪枝的核心技术，发展现状，未来展望以及学习资源推荐。

1 模型剪枝基础

1.1 什么是模型剪枝

深度学习网络模型从卷积层到全连接层存在着大量冗余的参数，大量神经元激活值趋近于 0，将这些神经元去除后可以表现出同样的模型表达能力，这种情况被称为过参数化，而对应的技术则被称为模型剪枝。

模型剪枝是一个新概念吗？并不是，其实我们从学习深度学习的第一天起就接触过，Dropout 和 DropConnect 代表着非常经典的模型剪枝技术，看下图。

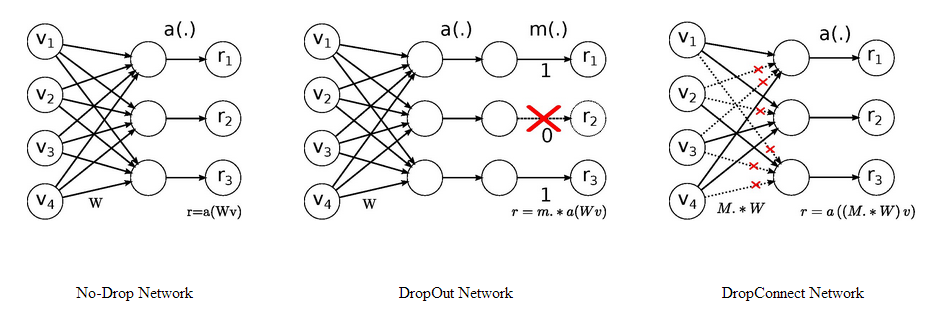
Dropout 中随机的将一些神经元的输出置零，这就是神经元剪枝。DropConnect 则随机的将一些神经元之间的连接置零，使得权重连接矩阵变得稀疏，这便是权重连接剪枝。它们就是最细粒度的剪枝技术，只是这个操作仅仅发生在训练中，对最终的模型不产生影响，因此没有被称为模型剪枝技术。

当然，模型剪枝不仅仅只有对神经元的剪枝和对权重连接的剪枝，根据粒度的不同，至少可以粗分为 4 个粒度。

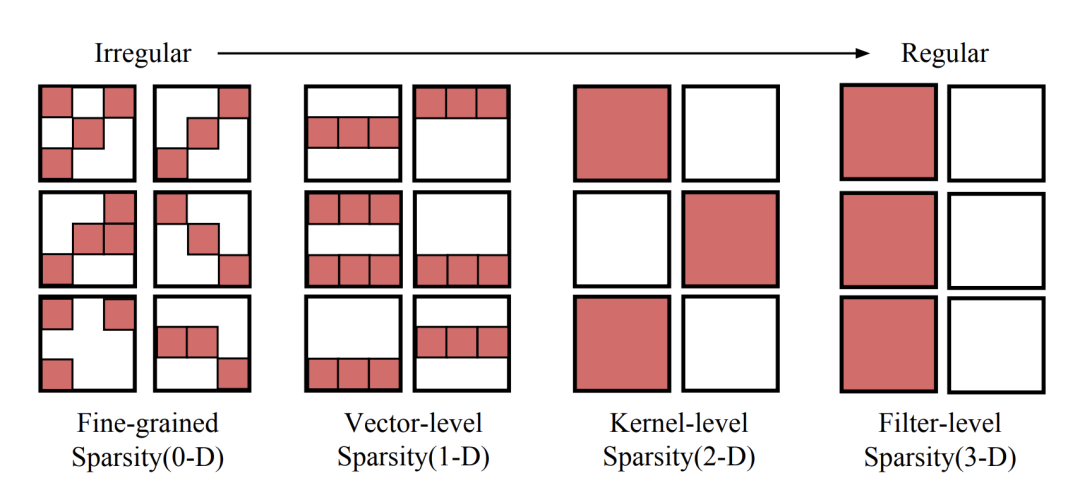
细粒度剪枝(fine-grained)：即对连接或者神经元进行剪枝，它是粒度最小的剪枝。

向量剪枝(vector-level)：它相对于细粒度剪枝粒度更大，属于对卷积核内部(intra-kernel)的剪枝。

核剪枝(kernel-level)：即去除某个卷积核，它将丢弃对输入通道中对应计算通道的响应。

滤波器剪枝(Filter-level)：对整个卷积核组进行剪枝，会造成推理过程中输出特征通道数的改变。

细粒度剪枝(fine-grained)，向量剪枝(vector-level)，核剪枝(kernel-level)方法在参数量与模型性能之间取得了一定的平衡，但是网络的拓扑结构本身发生了变化，需要专门的算法设计来支持这种稀疏的运算，被称之为非结构化剪枝。

而滤波器剪枝(Filter-level)只改变了网络中的滤波器组和特征通道数目，所获得的模型不需要专门的算法设计就能够运行，被称为结构化剪枝。除此之外还有对整个网络层的剪枝，它可以被看作是滤波器剪枝(Filter-level)的变种，即所有的滤波器都丢弃。

1.2 模型剪枝的必要性

既然冗余性是存在的，那么剪枝自然有它的必要性，下面以 Google 的研究来说明这个问题。

Google 在《To prune, or not to prune: exploring the efficacy of pruning for model compression》[1]中探讨了具有同等参数量的稀疏大模型和稠密小模型的性能对比，在图像和语音任务上表明稀疏大模型普遍有更好的性能。

它们对 Inception V3 模型进行了实验，在参数的稀疏性分别为 0%，50%，75%，87.5% 时，模型中非零参数分别是原始模型的 1，0.5，0.25，0.128 倍进行了实验。实验结果表明在稀疏性为 50% 时，Inception V3 模型的性能几乎不变。稀疏性为 87.5% 时，在 ImageNet 上的分类指标下降为 2%。

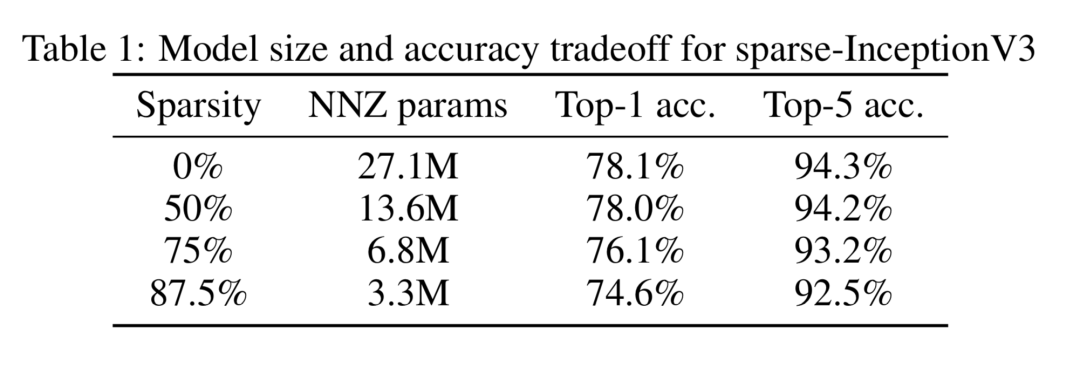
除了在大模型上的实验结果，还对小模型 MobileNet 也进行了实验，分别在同样大小参数量的情况下，比较了更窄的 MobileNet 和更加稀疏的 MobileNet 的分类指标，发现稀疏的 MobileNet 模型性能明显优于非稀疏的 MobileNet 模型。

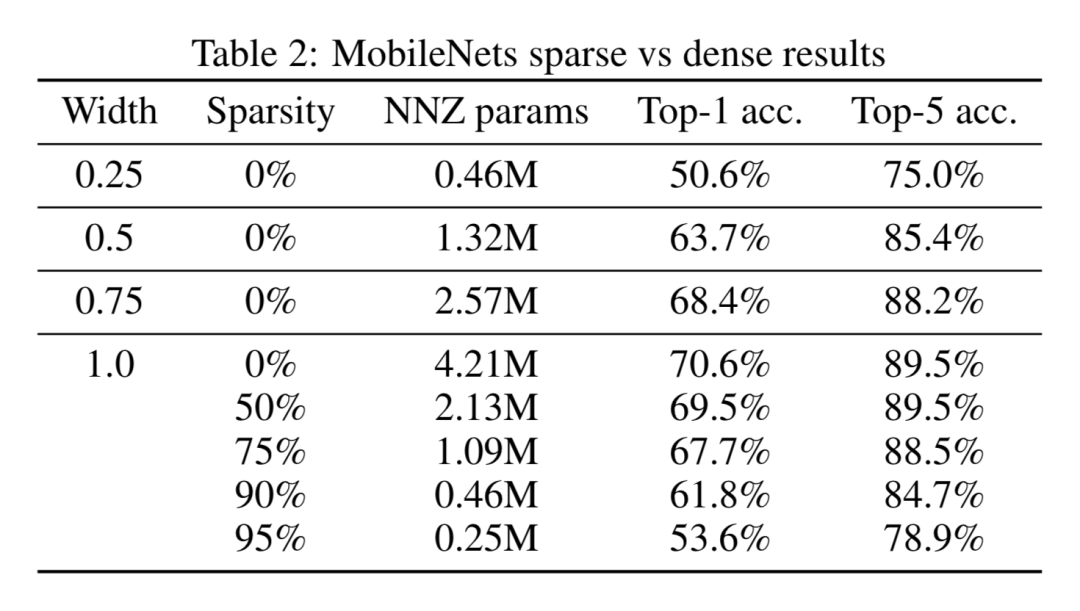
具体来说，稀疏率为 75% 的模型比宽度为原始 MobileNet 的 0.5 倍的模型在 ImageNet 分类任务的 top-1 指标上高出了 4%，而且模型的体积更小。稀疏率为 90% 的模型比宽度为原始 MobileNet 的 0.25 倍的模型在 ImageNet 分类任务的 top-1 指标上高出了 10%，而两者的模型大小相当。

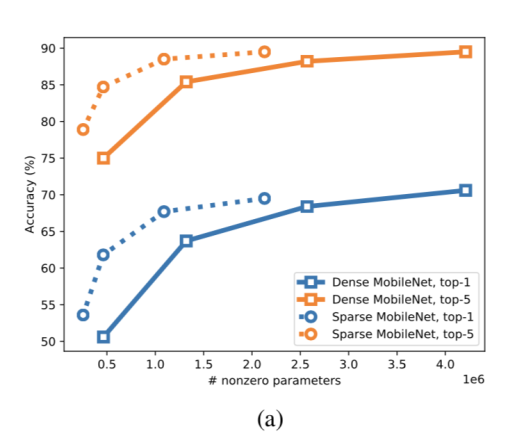
因此，我们完全可以相信，模型剪枝是有效的而且是必要的，剩下的问题就是怎么去找到冗余的参数进行剪枝。

2 模型剪枝算法

模型剪枝算法根据剪枝的处理策略来说，可以分为对模型进行稀疏约束然后进行训练后的剪枝，在模型的训练过程中进行剪枝，以及在模型训练之前就进行剪枝。而根据粒度的不同，流行的剪枝算法是细粒度的权重连接剪枝和粗粒度的通道/滤波器剪枝。

这些方法各自有交叉，无法完全分开，下面我们就基于两大不同的粒度来介绍一些训练中剪枝的代表性方法，而不再单独介绍稀疏约束以及训练前剪枝方法，相关内容感兴趣的读者可以去有三 AI 知识星球中阅读。

2.1 细粒度剪枝核心技术(连接剪枝)

对权重连接和神经元进行剪枝是最简单，也是最早期的剪枝技术，下图展示的就是一个剪枝前后对比，剪枝内容包括了连接和神经元。

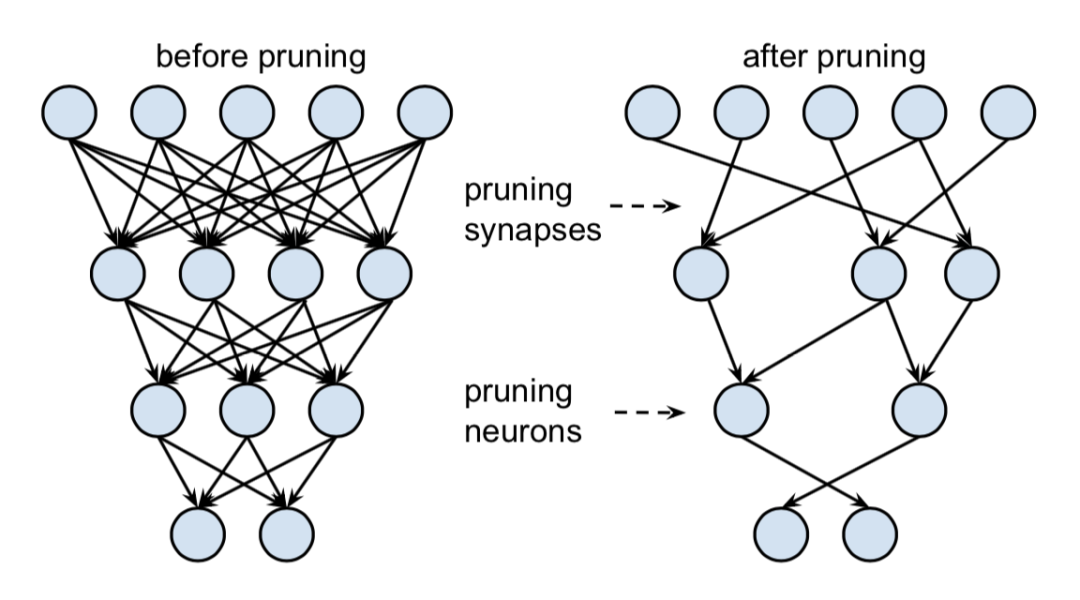
这一类技术的整体步骤如下：

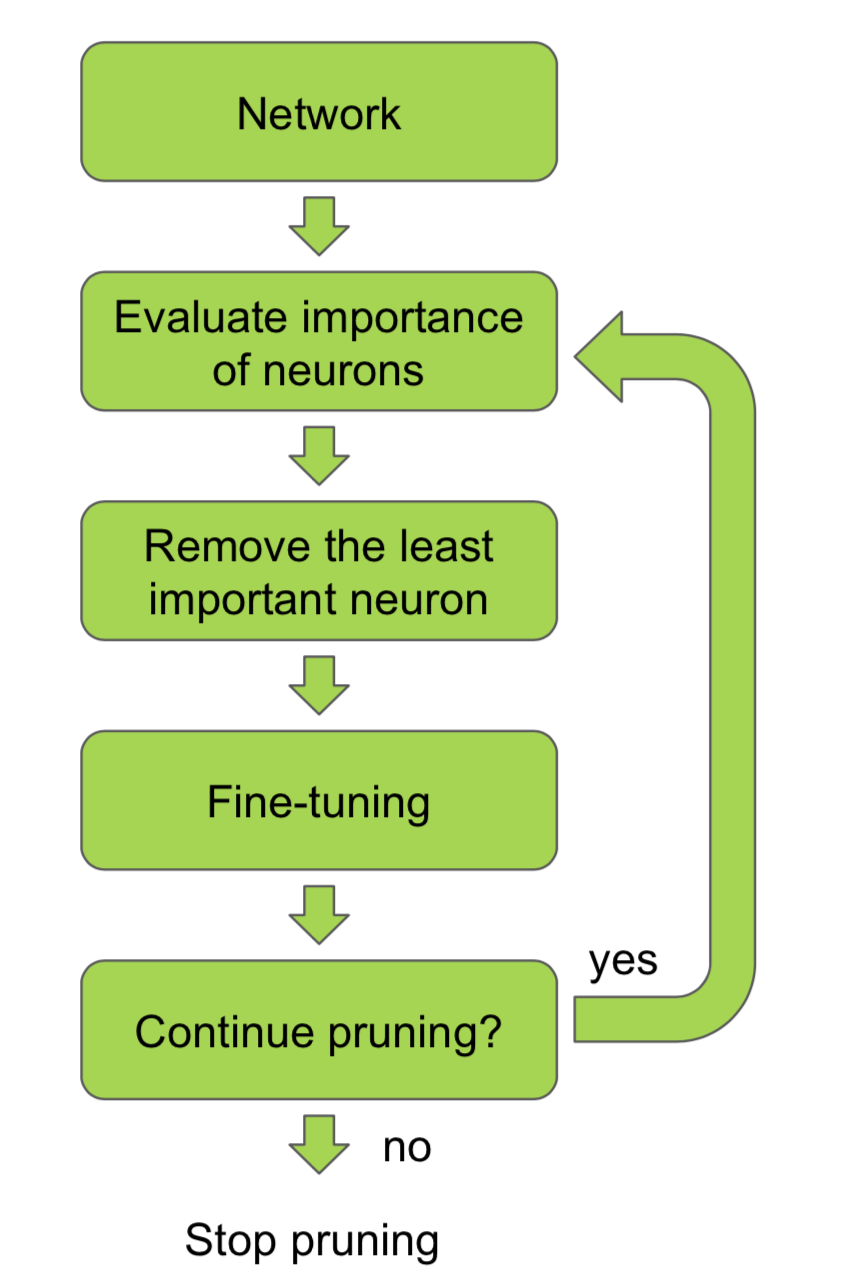
其中重点在于两个，一个是如何评估一个连接的重要性，另一个是如何在剪枝后恢复模型的性能。

对于评估连接的重要性，这里我们介绍两个最典型的方法代表，其一是基于连接幅度的方法[2]，其二是基于损失函数的方法[3]。

由于特征的输出是由输入与权重相乘后进行加权，权重的幅度越小，对输出的贡献越小，因此一种最直观的连接剪枝方法就是基于权重的幅度，如 L1/L2 范数的大小。这样的方法只需要三个步骤就能完成剪枝：

第一步：训练一个基准模型。

第二步：对权重值的幅度进行排序，去掉低于一个预设阈值的连接，得到剪枝后的网络。

第三步：对剪枝后网络进行微调以恢复损失的性能，然后继续进行第二步，依次交替，直到满足终止条件，比如精度下降在一定范围内。

这一类方法原理简单，前述提到的 Google 的方法也属于这一类。当然这类框架还有可以改进之处，比如 Dynamic network surgery 框架[4]观察到一些在当前轮迭代中虽然作用很小，但是在其他轮迭代中又可能重要，便在剪枝的基础上增加了一饿 spliciing 操作，即对一些被剪掉的权重进行恢复，如下：

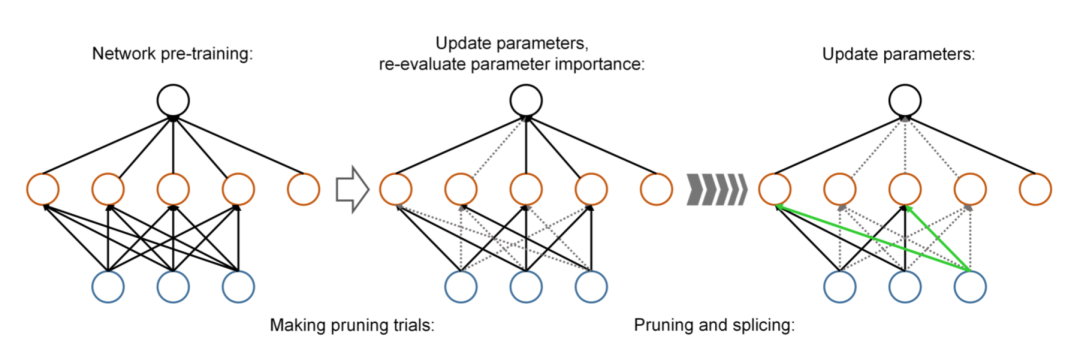
基于权重幅度的方法原理简单，但这是比较主观的经验，即认为权重大就重要性高，事实上未必如此。而另一种经典的连接剪枝方法就是基于优化目标，根据剪枝对优化目标的影响来对其重要性进行判断，以最优脑损伤(Optimal Brain Damage, OBD)[3]方法为代表，这已经是上世纪 90 年代的技术了。

Optimal Brain Damage 首先建立了一个误差函数的局部模型来预测扰动参数向量对优化目标造成的影响。具体来说用泰勒级数来近似目标函数 E，参数向量 U 的扰动对目标函数的改变使用泰勒展开后如下：

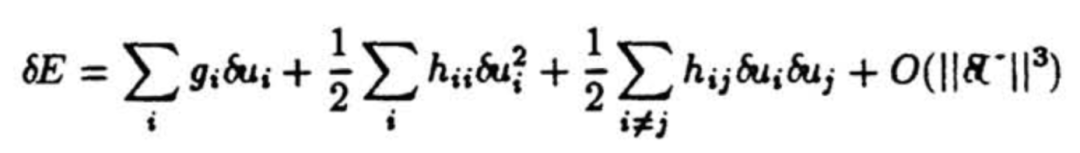
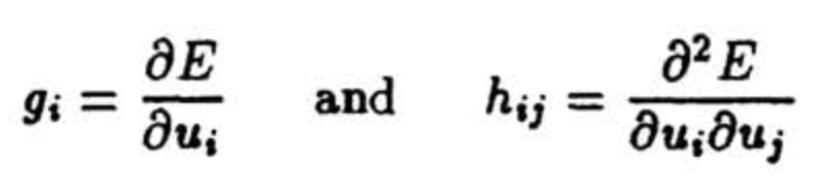
其中 g_i 是优化目标对参数 u 的梯度，而 h 是优化目标对参数 u 的海森矩阵。对模型剪枝的过程是希望找到一个参数集合，使得删除掉这个参数集合之后损失函数 E 的增加最小，由于上面的式子需要求解损失函数的海森矩阵 H，这是一个维度为参数量平方的矩阵，几乎无法进行求解，为此需要对问题进行简化，这建立在几个基本假设的前提上：

(1) 参数独立。即删除多个参数所引起的损失的改变，等于单独删除每个参数所引起的损失改变的和，因此上式第三项可以去除。

(2) 局部极值。即剪枝是发生在模型已经收敛的情况下，因此第一项可以去除，并且 hii 都是正数，即剪枝一定会带来优化目标函数的增加，或者说带来性能的损失。

(3) 二次近似假定。即上式关系为二次项，最后一项可以去除。

经过简化后只剩下了第二项，只需要计算 H 矩阵的对角项。它可以基于优化目标对连接权重的导数进行计算，复杂度就与梯度计算相同了，如下：

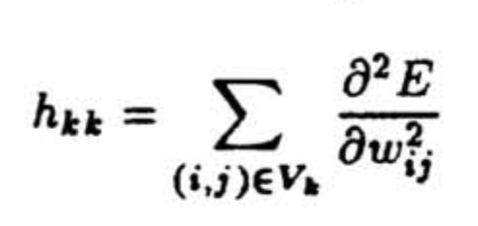
计算完之后就可以得到连接对优化目标改变的贡献，这就是它的重要性，因此可以进行剪枝，整个流程如下：

基于优化目标的权重剪枝方法还有很多，感兴趣的可以移步有三 AI 知识星球中的模型压缩板块。

2.2 粗粒度剪枝核心技术(通道剪枝)

相对于连接权重剪枝，粗粒度剪枝其实更加有用，它可以得到不需要专门的算法支持的精简小模型。对滤波器进行剪枝和对特征通道进行剪枝最终的结果是相同的，篇幅有限我们这里仅介绍特征通道的剪枝算法代表。

通道剪枝算法有三个经典思路。第一个是基于重要性因子，即评估一个通道的有效性，再配合约束一些通道使得模型结构本身具有稀疏性，从而基于此进行剪枝。第二个是利用重建误差来指导剪枝，间接衡量一个通道对输出的影响。第三个是基于优化目标的变化来衡量通道的敏感性。下面我们重点介绍前两种。

Network Trimming[5]通过激活的稀疏性来判断一个通道的重要性，认为拥有更高稀疏性的通道更应该被去除。它使用 batch normalization 中的缩放因子γ来对不重要的通道进行裁剪，如下图：

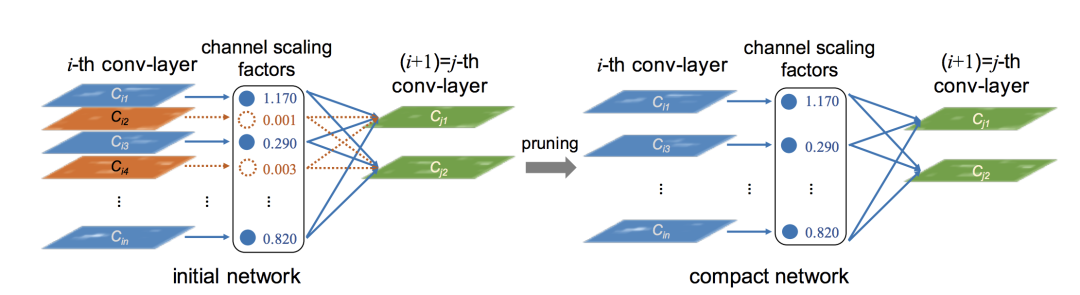
具体实现起来，就是在目标方程中增加一个关于γ的正则项，从而约束某些通道的重要性。

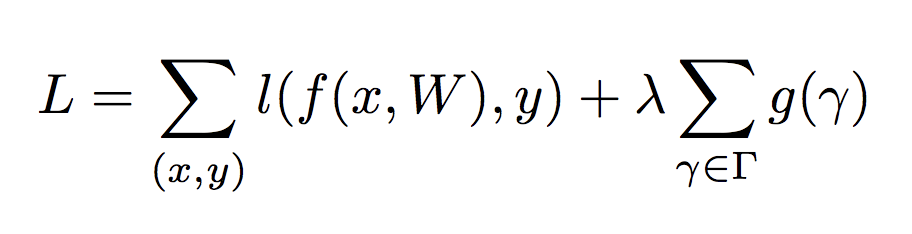
类似的框架还有《Rethinking the smaller-norm-less-informative assumption in channel pruning of convolution layers》[6]，《Data-Driven Sparse Structure Selection》[7]，读者感兴趣可以自己学习或者移步有三 AI 知识星球。

与基于权重幅度的方法来进行连接剪枝一样，基于重要性因子的方法主观性太强，而另一种思路就是基于输出重建误差的通道剪枝算法[8]，它们根据输入特征图的各个通道对输出特征图的贡献大小来完成剪枝过程，可以直接反映剪枝前后特征的损失情况。

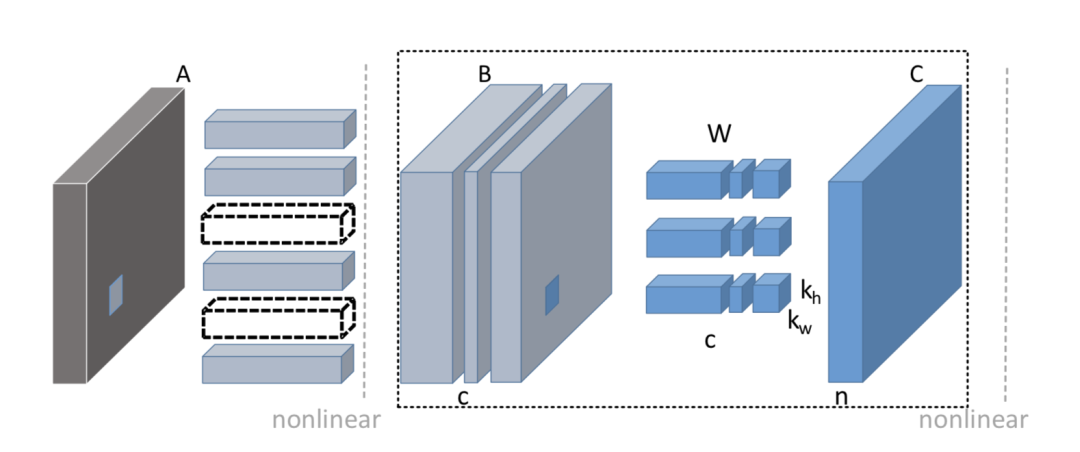
如上图，基于重建误差的剪枝算法，就是在剪掉当前层 B 的若干通道后，重建其输出特征图 C 使得损失信息最小。假如我们要将 B 的通道从 c 剪枝到 c’，要求解的就是下面的问题，第一项是重建误差，第二项是正则项。

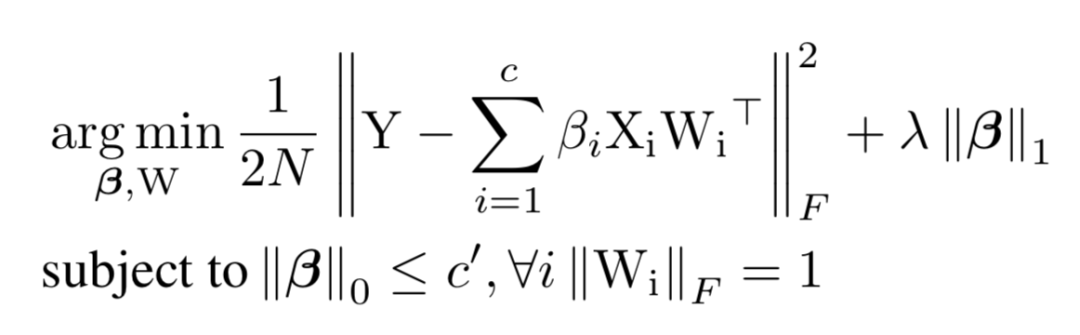
该问题可以分两步进行求解。

第一步：选择候选的裁剪通道。

我们可以对输入特征图按照卷积核的感受野进行多次随机采样，获得输入矩阵 X，权重矩阵 W，输出 Y。然后将 W 用训练好的模型初始化，逐渐增大正则因子，每一次改变都进行若干次迭代，直到 beta 稳定，这是一个经典的 LASSO 回归问题求解。

第二步：固定 beta 求解 W，完成最小化重建误差，需要更新使得下式最小。

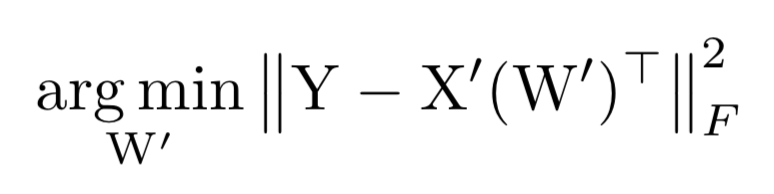
以上两个步骤交替进行优化，最后迭代完剪枝后，就可以得到新的权重。类似的框架还有 ThiNet[9]等，�