Embedding 技术概览：

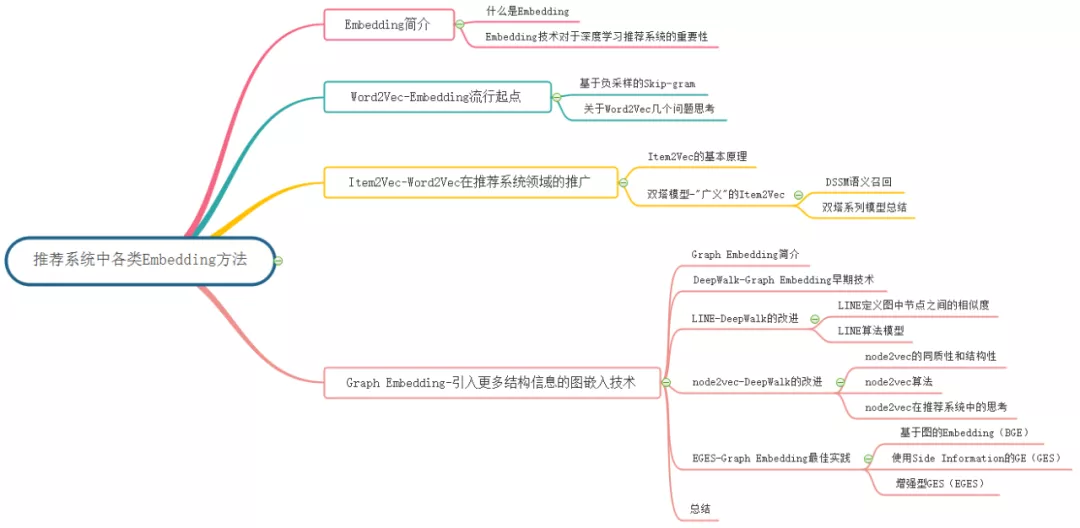
对其它 Embedding 技术不熟悉，可以看我的上一篇文章：

深度学习推荐系统中各类流行的 Embedding 方法（上）

1. Graph Embedding 简介

Word2Vec 和其衍生出的 Item2Vec 类模型是 Embedding 技术的基础性方法，二者都是建立在“序列”样本（比如句子、用户行为序列）的基础上的。在互联网场景下，数据对象之间更多呈现的是图结构，所以 Item2Vec 在处理大量的网络化数据时往往显得捉襟见肘，在这样的背景下，Graph Embedding 成了新的研究方向，并逐渐在深度学习推荐系统领域流行起来。

Graph Embedding 也是一种特征表示学习方式，借鉴了 Word2Vec 的思路。在 Graph 中随机游走生成顶点序列，构成训练集，然后采用 Skip-gram 算法，训练出低维稠密向量来表示顶点。之后再用学习出的向量解决下游问题，比如分类，或者连接预测问题等。可以看做是两阶段的学习任务，第一阶段先做无监督训练生成表示向量，第二阶段再做有监督学习，解决下游问题。

总之，Graph Embedding 是一种对图结构中的节点进行 Embedding 编码的方法。最终生成的节点 Embedding 向量一般包含图的结构信息及附近节点的局部相似性信息。不同 Graph Embedding 方法的原理不尽相同，对于图信息的保留方式也有所区别，下面就介绍几种主流的 Graph Embedding 方法和它们之间的区别与联系。

2. DeepWalk-Graph Embedding 早期技术

早期，影响力较大的 Graph Embedding 方法是于 2014 年提出的 DeepWalk，它的主要思想是在由物品组成的图结构上进行随机游走，产生大量物品序列，然后将这些物品序列作为训练样本输入 Word2Vec 进行训练，得到物品的 Embedding。因此，DeepWalk 可以被看作连接序列 Embedding 和 Graph Embedding 的过渡方法。

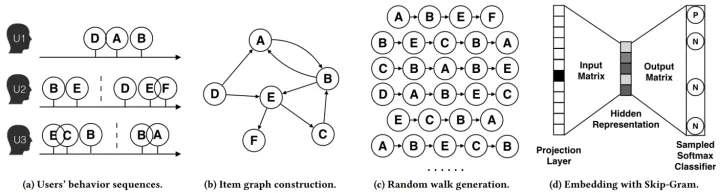
论文《Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba》用上图所示的方法展现了 DeepWalk 的算法流程。DeepWalk 算法的具体步骤如下：

  • 图（a）是原始的用户行为序列。
  • 图（b）基于这些用户行为序列构建了物品关系图。可以看出，物品 A 和 B 之间的边产生的原因是用户 U1 先后购买了物品 A 和物品 B。如果后续产生了多条相同的有向边，则有向边的权重被加强。在将所有用户行为序列都转换成物品关系图中的边之后，全局的物品关系图就建立起来了。
  • 图（c）采用随机游走的方式随机选择起始点，重新产生物品序列。
  • 将这些物品序列输入图（d）所示的 Word2Vec 模型中，生成最终的物品 Embedding 向量。

在上述 DeepWalk 的算法流程中，唯一需要形式化定义的是随机游走的跳转概率，也就是到达结点 v_i 后，下一步遍历 v_i 的邻接点 v_j 的概率。如果物品关系图是有向有权图，那么从节点 v_i 跳转到节点 v_j 的概率定义如下式所示。

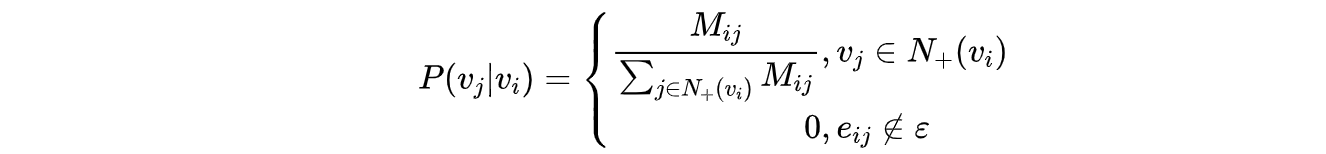
其中 \epsilon 是物品关系图中所有边的集合，N_+(v_i) 是节点v_i 所有的出边集合，M_{ij} 是节点 v_i 到节点v_j 边的权重，即 DeepWalk 的跳转概率就是跳转边的权重占所有相关出边权重之和的比例。

如果物品关系图是无向无权图，那么跳转概率将是上式的一个特例，即权重M_{ij} 将为常数 1，且 N_+(v_i) 应是节点v_i 所有“边”的集合，而不是所有“出边”的集合。

注意： 在 DeepWalk 论文中，作者只提出 DeepWalk 用于无向无权图。DeepWalk 用于有向有权图的内容是阿里巴巴论文《Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba》中提出的 Base Graph Embedding（BGE）模型，其实该模型就是对 DeepWalk 模型的实践，本文后边部分会讲解该模型。

DeepWalk 相关论文：

【1】Perozzi B, Alrfou R, Skiena S, et al. DeepWalk: online learning of social representations[C]. knowledge discovery and data mining, 2014: 701-710.

【2】Wang J, Huang P, Zhao H, et al. Billion-scale Commodity Embedding for E-commerce Recommendation in Alibaba[C]. knowledge discovery and data mining, 2018: 839-848.

3. LINE-DeepWalk 的改进

DeepWalk 使用 DFS（Deep First Search，深度优先搜索）随机游走在图中进行节点采样，使用 Word2Vec 在采样的序列上学习图中节点的向量表示。LINE（Large-scale Information Network Embedding）也是一种基于邻域相似假设的方法，只不过与 DeepWalk 使用 DFS 构造邻域不同的是，LINE 可以看作是一种使用 BFS（Breath First Search，广度优先搜索）构造邻域的算法。

在 Graph Embedding 各个方法中，一个主要区别是对图中顶点之间的相似度的定义不同，所以先看一下 LINE 对于相似度的定义。

3.1 LINE 定义图中节点之间的相似度

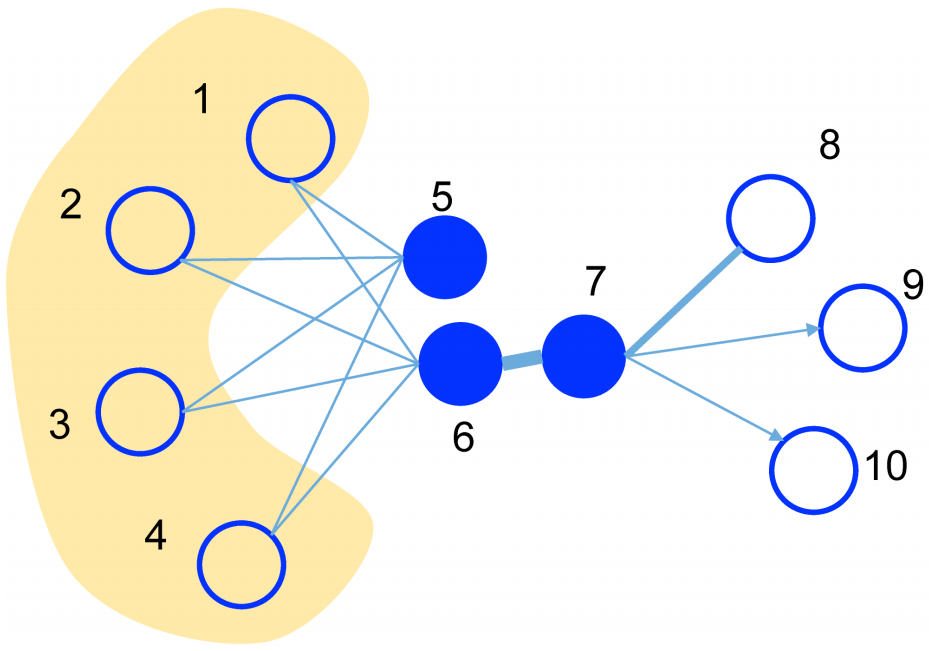
现实世界的网络中，相连接的节点之间存在一定的联系，通常表现为比较相似或者在向量空间中距离接近。对于带权网络来说，节点之间的权越大，相似度会越高或者距离越接近，这种关系称为 一阶近邻。一阶近邻关系用于描述图中相邻顶点之间的局部相似度， 形式化描述为若顶点u、v之间存在直连边，则边权w_{uv}即为两个顶点的相似度，若不存在直连边，则一阶相似度为 0。如下图所示，6 和 7 之间存在直连边，且边权较大（表现为图中顶点之间连线较粗），则认为两者相似且一阶相似度较高，而 5 和 6 之间不存在直连边，则两者间一阶相似度为 0。

但是，网络中的边往往比较稀疏，仅仅依靠一阶近邻关系，难以描述整个网络的结构。论文中定义了另外一种关系叫做 二阶近邻。例如下图中的网络，节点 5 和节点 1,2,3,4相连，节点6也和节点 1,2,3,4 相连，虽然节点 5 和 6 之间没有直接联系，但是节点 5 和 6 之间很可能存在某种相似性。举个例子，在社交网络中，如果两个人的朋友圈重叠度很高，或许两个人之间具有相同的兴趣并有可能成为朋友；在 NLP 中，如果不同的词经常出现在同一个语境中，那么两个词很可能意思相近。

LINE 通过捕捉网络中的一阶近邻关系和二阶近邻关系，更加完整地描述网络。并且 LINE 适用于有向图、无向图、有权图、无权图。

3.2 LINE 算法模型

（1）一阶近邻关系模型

一阶近邻关系模型中定义了两个概率，一个是联合概率，如下公式所示：

p_1(v_i, v_j) = \frac1 {1 + exp( - \vec{u}^{T}_i \cdot \vec{ u}_j)}

其中， \vec u_i 是图中节点v_i 的向量表示，上式表示节点 v_i和 v_j 之间的相似程度，这是一个 sigmoid 函数。

另外一个是经验概率，如下公式所示：

\hat{p}_1(i,j)=\frac{w_{ij}}{W} , W=\sum_{(i,j)\in E} w_{ij}

其中， w_{ij}是节点v_i 和 v_j 之间的权重。优化目标为最小化下式：

O_1=d(\hat{p}_1(\cdot,\cdot),p_1(\cdot,\cdot))

其中，d(\cdot,\cdot)是两个分布的距离，目标是期望两个概率分布接近，利用 KL 散度来计算相似性，丢掉常数项之后，得到下面公式：

O_1=-\sum_{(i,j)\in E}w_{ij}\log{p_1(v_i,v_j)}

一阶近邻关系模型的优化目标就是最小化 O_1 。可以看到，上面这些公式无法表达方向概念，因此一阶近邻关系模型只能描述无向图。

2）二阶近邻关系模型

二阶近邻关系描述的是节点与邻域的关系，每个节点有两个向量，一个是该顶点本身的表示向量，一个是该顶点作为其他顶点的邻居时的表示向量，因此论文中对每个节点定义了两个向量， \vec u_i表示节点i本身， \vec u_i ’ 是节点j作为邻居的向量表示。针对每一个从节点i到j的有向边(i,j) ，定义一个条件概率，如下式：

p_2(v_j|v_i)=\frac {exp(\vec{u}_j’^{T} \cdot \vec{u}_i)} {\sum_{k=1}^{|V|} exp(\vec{u}_k’^{T} \cdot \vec{u}_i)}

其中，|V|是图中所有的节点数量，这其实是一个softmax函数。同样，还有一个经验概率，如下式：

\hat {p}_2(v_j|v_i)=\frac {w_{ij}} {d_i}, d_i=\sum_{k\in N(i)}w_{ik}

其中，w_{ij} 是边(i,j)的边权，d_i是从顶点v_i出发指向邻居节点的所有边权之和，N(i)是从节点i出发指向邻居的所有边集合。同样需要最小化条件概率和经验概率之间的距离，优化目标为：

O_2=\sum _{i \in V}\lambda_i d(\hat p_2(\cdot |v_i), p_2(\cdot|v_i))

其中，\lambda_i为控制节点重要性的因子，可以通过顶点的度数或者 PageRank 等方法估计得到。假设度比较高的节点权重较高，令 \lambda_i=d_i ，采用 KL 散度来计算距离，略去常数项后，得到公式：

O_2=-\sum_{(i,j) \in E} w_{ij}logp_2(v_j|v_i)

直接优化上式计算复杂度很高，每次迭代需要对所有的节点向量做优化，论文中使用 Word2Vec 中的负采样方法，得到二阶近邻的优化目标，如下公式所示。从计算的过程可以看到，二阶相似度模型可以描述有向图。

O_2=-\sum _{(i,j) \in E} w_{ij} \cdot (log\sigma(\vec{u}’^{T}_j \cdot \vec{u}_i) + \sum _{i=1}^{K} E_{v_n\sim P_n(v)}[log \sigma(- \vec{u}’^{T}_n \cdot \vec{u}_i)])

对比一阶近邻模型和二阶近邻模型的优化目标，差别就在于，二阶近邻模型对每个节点多引入了一个向量表示。实际使用的时候，对一阶近邻模型和二阶近邻模型分别训练，然后将两个向量拼接起来作为节点的向量表示。

此外有一点需要说明，在 Graph Embedding 方法中，例如 DeepWalk、Node2Vec、EGES，都是采用随机游走的方式来生成序列再做训练，而 LINE 直接用边来构造样本，这也是他们的一点区别。

LINE 论文：

【1】Tang J, Qu M, Wang M, et al. Line: Large-scale information network embedding[C]//Proceedings of the 24th international conference on world wide web. 2015: 1067-1077.

4. node2vec - DeepWalk 的改进

2016 年，斯坦福大学的研究人员在 DeepWalk 的基础上更进一步，提出了 node2vec 模型，它通过调整随机游走权重的方法使 Graph Embedding 的结果更倾向于体现网络的同质性（homophily）或结构性（structural equivalence）。

4.1 node2vec 的同质性和结构性

具体的讲，网络的“同质性”指的是距离相近节点的 Embedding 应尽量近似，如下图所示，节点 u与其相连的节点s_1, s_2, s_3, s_4 的 Embedding 表达应该是接近的，这就是网络的“同质性”的体现。

“结构性”指的是结构上相似的节点 Embedding 应尽量近似，下图中节点U 和节点 s_6 都是各自局域网络的中心节点，结构上相似，其 Embedding 的表达也应该近似，这是“结构性”的体现。

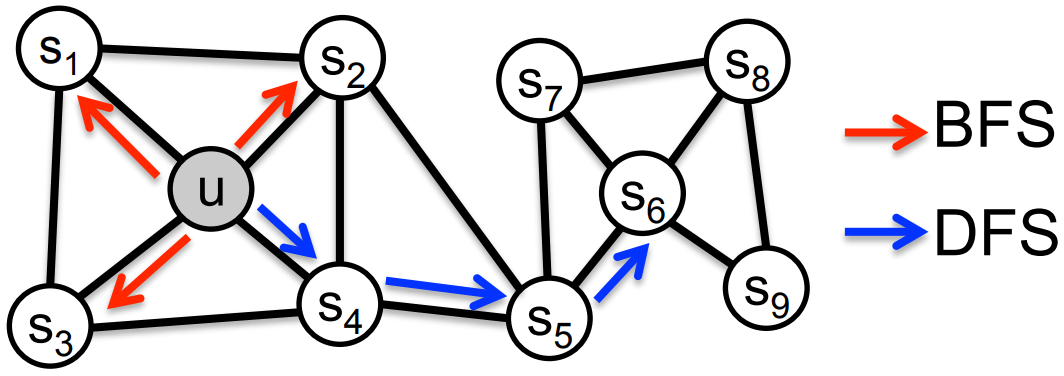
为了使 Graph Embedding 的结果能够表达网络的“结构性”，在随机游走过程中，需要让游走的过程更倾向于 BFS，因为 BFS 会更多地在当前节点的邻域中游走遍历，相当于对当前节点周边的网络结构进行一次“微观扫描”。当前节点是“局部中心节点”，还是“边缘节点”，或是“连接性节点”，其生成的序列包含的节点数量和顺序必然是不同的，从而让最终的 Embedding 抓取到更多结构性信息。

另外，为了表达“同质性”，需要让随机游走的过程更倾向于 DFS，因为 DFS 更有可能通过多次跳转，游走到远方的节点上，但无论怎样，DFS 的游走更大概率会在一个大的集团内部进行，这就使得一个集团或者社区内部的节点的 Embedding 更为相似，从而更多地表达网络的“同质性”。

但是在不同的任务中需要关注的重点不同，可能有些任务需要关注网络的 homophily，而有些任务比较关注网络的 structural equivalence，可能还有些任务两者兼而有之。在 DeepWalk 中，使用 DFS 随机游走在图中进行节点采样，使用 Word2Vec 在采样的序列学习图中节点的向量表示，无法灵活地捕捉这两种关系。

实际上，对于这两种关系的偏好，可以通过不同的序列采样方式来实现。有两种极端的方式，一种是 BFS，如上图中红色箭头所示，从 u 出发做随机游走，但是每次都只采样顶点 u 的直接邻域，这样生成的序列通过无监督训练之后，特征向量表现出来的是 structural equivalence 特性。另外一种是 DFS，如上图中蓝色箭头所示，从 u 出发越走越远，学习得到的特征向量反应的是图中的 homophily 关系。

4.2 node2vec 算法

那么在 node2vec 算法中，是怎么控制 BFS 和 DFS 的倾向性呢？主要是通过节点间的跳转概率。下图所示为 node2vec 算法从节点t跳转到节点v，再从节点v跳转到周围各点的跳转概率。假设从某顶点出发开始随机游走，第i-1步走到当前顶点v，要探索第i步的顶点x，如下图所示。下面的公式表示从顶点v到x的跳转概率，E是图中边的集合，(v,x)表示顶点v和x之间的边， \pi_{vx}表示从节点v跳转到下一个节点x的概率，Z是归一化常数。

带偏随机游走的最简单方法是基于下一个节点边权重 w_{vx} 进行采样，即 \pi_{vx}=w_{vx} ，是权重之和。对于无权重的网络，w_{vx}=1。最简单的方式，就是按照这个转移概率进行随机游走，但是无法控制 BFS 和 DFS 的倾向性。

P(c_i=x|c_{i-1}=v)=\begin{cases} \frac{\pi_{vx}}{Z} \quad if (v,x)\in E \\ 0 \quad otherwise \end{cases}

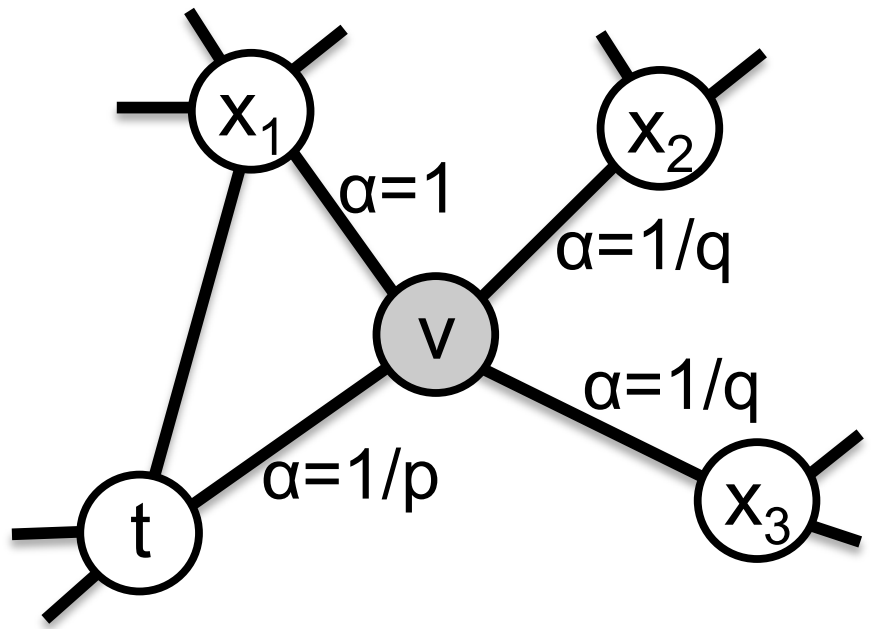
node2vec 用两个参数p和q定义了一个二阶随机游走，以控制随机游走的策略。假设当前随机游走经过边(t,v)到达顶点v，现在要决定从节点v跳转到下一个节点x，需要依据边(v,x)上的跳转概率\pi_{vx} 。设\pi_{vx}=\alpha_{pq}(t,x)\cdot w_{vx}，w_{vx}是顶点v和x之间的边权；\alpha_{pq}(t,x)是修正系数，定义如下：

\alpha_{pq}(t,x)=\begin{cases} \frac{1}{p}, \quad if\quad d_{tx}=0\\1,\quad if \quad d_{tx}=1\\ \frac{1}{q},\quad if \quad d_{tx}=2 \end{cases}

上式中d_{tx}表示下一步顶点x和顶点t之间的最短距离，只有 3 种情况，如果又回到顶点t，那么d_{tx}=0；如果x和t直接相邻，那么d_{tx}=1；其他情况d_{tx}=2。参数p和q共同控制着随机游走的倾向性。参数p被称为返回参数（return parameter），控制着重新返回顶点t的概率。如果p>max(q,1)，那么下一步较小概率重新返回顶点t；如果p<max(q,1)，那么下一步会更倾向于回到顶点t，node2vec 就更注重表达网络的结构性。参数q被称为进出参数（in-out parameter），如果q>1，那么下一步倾向于回到t或者t的临近顶点，这接近于 BFS 的探索方式；如果q<1，那么下一步倾向于走到离t更远的顶点，接近于 DFS 寻路方式，node2vec 就更加注重表达网络的同质性。因此，可以通过设置p和q来控制游走网络的方式。所谓的二阶随机游走，意思是说下一步去哪，不仅跟当前顶点的转移概率有关，还跟上一步顶点相关。在论文中试验部分，作者对p和q的设置一般是 2 的指数，比如\{\frac{1}{4},\frac{1}{2},1,2,4\}。

node2vec 这种灵活表达同质性和结构性的特点也得到了实验的证实，通过调整参数和产生了不同的 Embedding 结果。下图中的上半部分图片就是 node2vec 更注重同质性的体现，可以看到距离相近的节点颜色更为接近，下图中下半部分图片则更注重体现结构性，其中结构特点相近的节点的颜色更为接近。

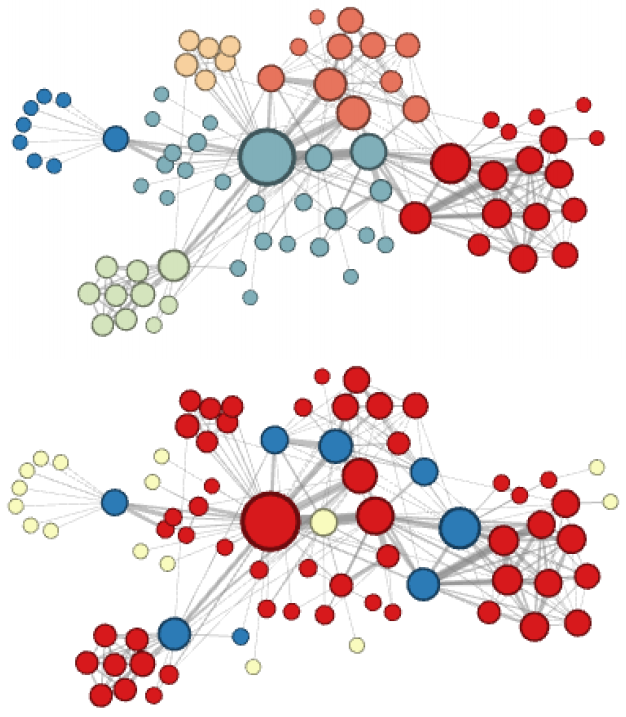
4.3 node2vec 在推荐系统中的思考

node2vec 所体现的网络的同质性和结构性在推荐系统中可以被很直观的解释。同质性相同的物品很可能是同品类、同属性，或者经常被一同购买的商品，而结构性相同的物品则是各品类的爆款、各品类的最佳凑单商品等拥有类似趋势或者结构性属性的商品。毫无疑问，二者在推荐系统中都是非常重要的特征表达。由于 node2vec 的这种灵活性，以及发掘不同图特征的能力，甚至可以把不同 node2vec 生成的偏向“结构性”的 Embedding 结果和偏向“同质性”的 Embedding 结果共同输入后续的深度学习网络，以保留物品的不同图特征信息。

node2vec 论文：

【1】Grover A, Leskovec J. node2vec: Scalable feature learning for networks[C]//Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining. 2016: 855-864.

5. EGES - Graph Embedding 最佳实践

2018 年，阿里巴巴公布了其在淘宝应用的 Embedding 方法 EGES（Enhanced Graph Embedding with Side Information）算法，其基本思想是 Embedding 过程中引入带权重的补充信息（Side Information），从而解决冷启动的问题。

淘宝平台推荐的三个问题：

  • 可扩展性(scalability)：已有的推荐算法(CF、Base-Content、DL)可以在小数据集上有不错效果，但是对于 10 亿用户和 20 亿商品这样海量的数据集上效果差。
  • 稀疏性(sparsity)：用户仅与小部分商品交互，难以训练准确的推荐模型。
  • 冷启动(cold start)：物品上新频繁，然而这些商品并没有用户行为，预测用户对这些商品的偏好是十分具有挑战性的。

现在业界针对海量数据的推荐问题通用框架是分成两个阶段，即 matching 和 ranking。在 matching 阶段，我们会生成一个候选集，它的 items 会与用户接触过的每个 item 具有相似性；接着在 ranking 阶段，我们会训练一个深度神经网络模型，它会为每个用户根据他的偏好对候选 items 进行排序。论文关注的问题在推荐系统的 matching 阶段，也就是从商品池中召回候选商品的阶段，核心的任务是计算所有 item 之间的相似度。

为了达到这个目的，论文提出根据用户历史行为构建一个 item graph，然后使用 DeepWalk 学习每个 item 的 embedding，即 Base Graph Embedding（BGE）。BGE 优于 CF，因为基于 CF 的方法只考虑了在用户行为历史上的 items 的共现率，但是对于少量或者没有交互行为的 item，仍然难以得到准确的 embedding。为了减轻该问题，论文提出使用 side information 来增强 embedding 过程，提出了 Graph Embedding with Side information (GES)。例如，属于相似类别或品牌的 item 的 embedding 应该相近。在这种方式下，即使 item 只有少量交互或没有交互，也可以得到准确的 item embedding。在淘宝场景下，side information 包括：category、brand、price 等。不同的 side information 对于最终表示的贡献应该不同，于是论文进一步提出一种加权机制用于学习 Embedding with Side Information，称为 Enhanced Graph Embedding with Side information (EGES)。

5.1 基于图的 Embedding（BGE）

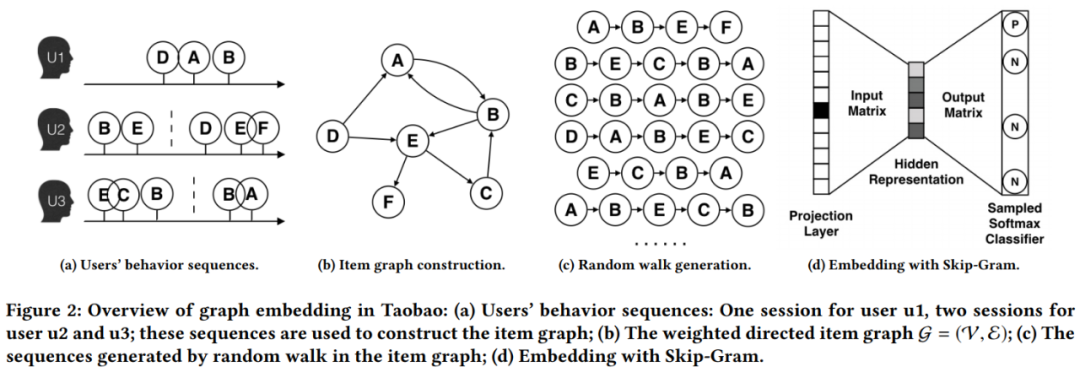
该方案是 DeepWalk 算法的实践，具体流程如下：

  • 首先，我们拥有上亿用户的行为数据，不同的用户，在每个 Session 中，访问了一系列商品，例如用户 u2 两次访问淘宝，第一次查看了两个商品 B-E，第二次产看了三个商品 D-E-F。
  • 然后，通过用户的行为数据，我们可以建立一个商品图（Item Graph），可以看出，物品 A，B 之间的边产生的原因就是因为用户 U1 先后购买了物品 A 和物品 B，所以产生了一条由 A 到 B 的有向边。如果后续产生了多条相同的有向边，则有向边的权重被加强。在将所有用户行为序列都转换成物品相关图中的边之后，全局的物品相关图就建立起来了。
  • 接着，通过 Random Walk 对图进行采样，重新获得商品序列。
  • 最后，使用 Skip-gram 模型进行 Embedding 。

Base Graph Embedding 与 DeepWalk 不同的是：通过 user 的行为序列构建网络结构，并将网络定义为有向有权图。 其中：根据行为的时间间隔，将一个 user 的行为序列分割为多个 session。session 分割可以参考 Airbnb 这篇论文《Real-time Personalization using Embeddings for Search Ranking at Airbnb》。

5.2 使用 Side Information 的 GE（GES）

通过使用 BGE，我们能够将 items 映射到高维向量空间，并考虑了 CF 没有考虑的用户序列关系。但是我们依然没有解决冷启动的问题。为了解决冷启动问题，我们使用边信息（ category, shop, price, etc）赋值给不同的 item。因为边信息相同的两个 item，理论而言会更接近。通过 DeepWalk 方案得到 item 的游走序列，同时得到对应的边信息（category，brand，price）序列。然后将所有序列放到 Word2Vec 模型中进行训练。针对每个 item，将得到：item_embedding，category_embedding，brand_embedding，price_embedding 等 embedding 信息。为了与之前的 item embedding 区分开，在加入 Side information 之后，我们称得到的 embedding 为商品的 aggregated embeddings。商品 v 的 aggregated embeddings 为：

H_v = \frac{1}{n+1}\sum_{s=0}^{n}W_{v}^{s}

对上式做一个简单的解释：针对每个 item，将得到：item_embedding，category_embedding，brand_embedding，price_embedding 等 embedding 信息。将这些 embedding 信息求均值来表示该 item 的 Embedding。

需要注意的一点是， item 和 side information（例如 category, brand, price 等） 的 Embedding 是通过 Word2Vec 算法一起训练得到的。 如果分开训练，得到的 item_embedding 和 category_embedding、brand_embedding、price_embedding 不在一个向量空间中，做运算无意义。即：通过 DeepWalk 方案得到 item 的游走序列，同时得到对应的{category, brand, price}序列。然后将所有序列数据放到 Word2Vec 模型中进行训练。

5.3 增强型 GES（EGES）

GES 中存在一个问题是，针对每个 item，它把所有的 side information embedding 求和后做了平均，没有考虑不同的 side information 之间的权重，EGES 就是让不同类型的 side information 具有不同的权重，提出来一个加权平均的方法来聚集这些边界 embedding。

因为每个 item 对其不同边信息的权重不一样，所以就需要额外矩阵A来表示每个 item 边信息的权重，其大小为v*(n+1)，v是 item 的个数，n是边信息的个数，加 1 是还要考虑 item 自身 Embedding 的权重。为了简单起见，我们用a^j_v表示第v个 item、第j个类型的 side information 的权重。a^0_v表示第v个 item 自身 Embedding 的权重。这样就可以获得加权平均的方法：

H_v = \frac{\sum_{j=0}^{n}e^{a_{v}^{j}}W_{v}^{j}}{\sum_{j=0}^{n}e^{a_{v}^{j}}}

这里对权重项a^j_v做了指数变换，目的是为了保证每个边信息的贡献都能大于 0。权重矩阵A通过模型训练得到。

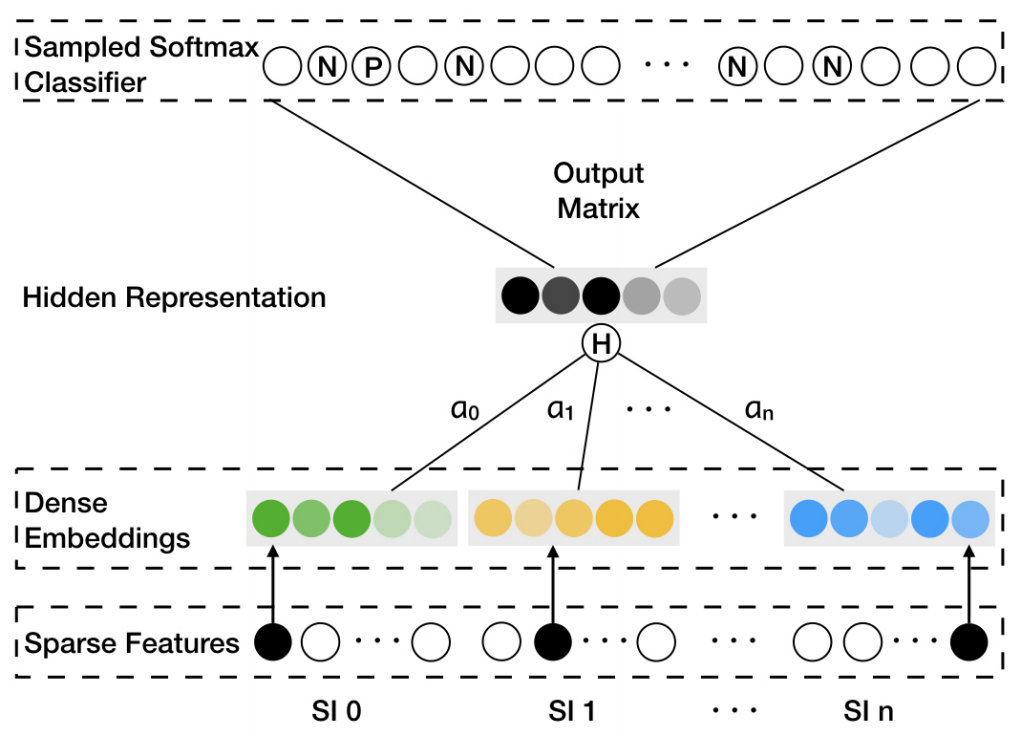
EGES 算法应用改进的 Word2Vec 算法（Weighted Skip-Gram）确定模型的参数。对上图中 EGES 算法简单说明如下：

  • 上图的 Sparse Features 代表 item 和 side information 的 ID 信息；
  • Dense Embeddings 表示 item 和 side information 的 embedding 信�