理解计算从根号到第季神经网络的数学模型
1910年,英国哲学家伯特兰·罗素(Bertrand Russell )和其老师怀特海(Alfred North Whitehead)合著的《数学原理》一书问世,这本书是如此的深奥,尤其对中国人而言,因为直到100多年后的今天,仍然没有完整而权威的中译本(能看懂的人确实很少)。不过想想现在连一般的科普作品都翻译得如此垃圾,我们真应该庆幸。这本不朽的名著为两个年纪相差25岁的科学家建立了一条联系一生的纽带,同时也为神经计算提供了最初的思想来源。
沃尔特·皮茨(Walter Pitts)是很多取得巨大成就但命运坎坷的科学家中的一员。12岁时经常被人欺负(家人和同学),作为一个孩子,他最幸福的时光是在图书馆里度过的。他曾花了三天时间读完了2000页的《数学原理》,并写信给罗素指出了书中的几处错误[1]。心胸宽广的罗素甚至邀请皮茨去剑桥大学当他的研究生。15岁时,皮茨离家出走,从此他就再也没有见过他的家人,他要到芝加哥大学寻找他的偶像罗素。在芝加哥大学,哲学家,自然语言处理的先驱鲁道夫·卡尔纳普(Rudolf Carnap)给了他很多帮助,为皮茨谋了打扫卫生的差事[2],这一幕简直就是现实版的《心灵捕手》。皮茨在旁听罗素的课的时候,结识了杰罗姆·莱特文(Jerome Lettvin),一名年轻的医学系学生。莱特文将皮茨介绍给了沃伦·麦卡洛克(Warren McCulloch),一位比皮茨年长25岁的教授,从此以后,来自不同经济阶层的两人一起生活、一起工作、甚至一起死亡。很快,他们将创造第一个关于精神的机械论理论——神经科学的第一种计算方法,现代计算机逻辑设计以及人工智能的支柱[1]。

图1 Walter Pitts (左)和 Warren McCulloch(右)
皮茨和麦卡洛克还有一个共同的偶像,戈特弗里德·莱布尼茨(Gottfried Leibniz),就是发明微积分的数学家莱布尼茨。作为哲学家或逻辑学家,他认为:“我们的所有观念(概念)都是由非常小数目的简单观念复合而成,它们形成了人类思维的基本单元:字母。复杂的观念来自这些简单的观念,是由它们通过模拟算术运算的统一的和对称的组合。” 这种复杂观念由符号所表示的基本单元进行逻辑计算的结果的思想,实际上也指导了《数学原理》创作。《原理》的宏大目标是通过用无可争论的简单的基本逻辑来建立整个数学体系。从命题入手,罗素和怀特海德采用了与、或、非三种基本逻辑运算来将命题连接成越来越复杂的网络。就是利用这些简单的命题,他们完整的推导出了整个复杂的现代数学。从《数学原理》开始,逻辑学从哲学中走出来,开始渗透到数学的各个方面,对计算领域产生了巨大的影响。
由于麦卡洛克本身就是一个神经生理学家,我们在第2季中介绍的关于神经元的结构和功能在当时是神经生理学开创性的工作,这个工作对麦卡洛克产生了深刻影响。当时已经知道的是大脑里的每一个神经细胞只会在达到某个阈值时才被激发, 也就是说必须有足够多的相邻神经细胞通过神经元的突触向它传递信号,它才会发放出自己的电脉冲,即“全或无法则”。对于也曾认真学习过《数学原理》的麦卡洛克来说,这种设置就是二元的,神经元只有激发和不激发两种状态。他发现神经元的信号就是一个命题,而神经元的工作类似于逻辑门,它接受多个输入然后产生单一的输出。通过改变神经元的激发阙值,就可以让它执行「与」、「或」以及「非」的函数(功能)[1]。
需要声明的是,生物学上的神经活动是非常复杂的,就神经元从突触分两种类型,一些是兴奋性的(excitatory),另一些则是抑制性(inhibitory)的,之前我介绍过,这是谢灵顿的发现。兴奋性和抑制性两类突触获得外界的刺激会让神经细胞产生两种状态,激活态或是非激活态,神经细胞被激活的话,则会沿着轴突产生一种脉冲信号,通过另一端的突触把刺激作用传递给其他神经细胞。实际上,我们要清醒地认识到,对于神经细胞而言,它可不认为自己有两种状态,它只是适时地发送脉冲信号给其他神经元罢了。这种脉冲信号的产生符合我们之前讲授“全或无”法则,也就是突触获得外界刺激要么使细胞产生脉冲,要么就不产生。还有一个关键问题是,触突的兴奋和抑制作用到底是如何综合产生影响的,这一点非常复杂。为了用数学工具模拟神经活动,必须进行简化。首先假设细胞是否产生脉冲对应于一个开关,这个开关只有两种状态:开和关,也就是二进制状态1或者0。其次,细胞接收到的输入刺激也只有0,1两种模式,真正发挥作用的是,处于“开(1)”状态的兴奋性的输入的个数与抑制性输入个数的关系。最简单的假设是只有一个抑制性的输入,而且它产生的作用要强于多个兴奋性输入的作用,也就是说抑制性输入为1时,神经细胞的输出状态只能是0,当抑制性输入为0时,则需要看兴奋性输入为1的个数是否超过一定阈值T,如果超过一定阈值T,神经细胞才真正产生脉冲,即输出的状态才能是1。阈值在这里起到的作用完全对应“全或无”准则,不过这里需要有一个抑制性输入作为前提,抑制性输入可以看作一种控制信号。需要指出的是,神经细胞响应输入带来的刺激也是需要一个时间过程,也就是在t时刻的输入刺激,将在t+1时刻产生输出。
我们接下来将会看到这些基本假设是如何与逻辑门产生联系,并会举出一个具体的例子来看看如何利用神经元来进行逻辑运算。实际上,我们只需要几个简单的神经元就可以表示最基本的逻辑门,包括「与」、「或」以及「非」,如下图所示的表示是由人工智能的先驱马文明斯基提出的,就是他将感知机和Rosenblatt推进了深渊。
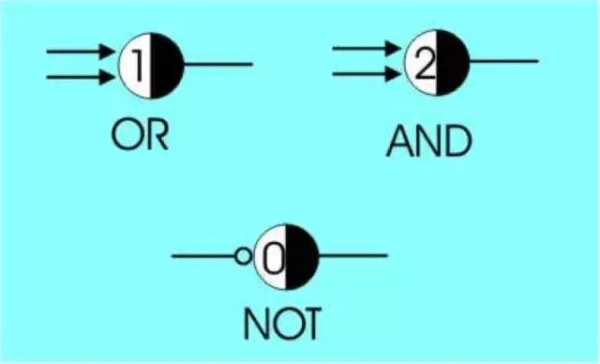
图2 神经元代表的逻辑门[4]
上面的每一个逻辑门就是一个神经元,例如,带箭头的输入表示兴奋性输入,以圆圈为端点的输入表示了抑制性输入,神经元中的数字(OR:1,AND:2,NOT:0)表示了这个神经元的阈值。以AND门为例,当两个兴奋性输入都为1时,他们的和大于等于阈值2,同时没有抑制性输入,因此神经元的输出就是1。当其中任意一个输入为0,输入的和将小于阈值2,因此将输出0。这就是利用神经元模拟AND门的。OR门与此类似,我们再看一下NOT门,在非门中存在一个抑制性输入,而没有兴奋性输入,并且阈值为0,抑制性输入为0,没有兴奋性输入,由于阈值为0,因此,将产生1的输出,而当抑制性输入为1的时候,神经元直接输出0,这个时候就根本不用计算了,这是一种规定。由于我们用神经元表示了基本的逻辑门,因此,我们也可以用神经元表示由基本逻辑门构建的任何东西。
我们又把延迟的时间因素忘记了,但这个延迟的时间是如此重要,它使得冯诺伊曼的存储程序计算机变的可能。我们可以通过叠加一些神经元来实现一个称之为延时门的逻辑门,如下图所示的的阈值为2的神经元,只看这单一的神经元的话,起初只有一个兴奋性输入,因此在下一时刻这个神经元的输出会是0。接下来,我们看下方另一个阈值为1的神经元,这个神经元一开始就有一个称为start的兴奋性输入(此时你仍可以忽略最下方的名为stop的抑制性输入),特别的是,这个神经元的输出又反馈给本身作为输入了。实际上,没有什么能够阻止神经元将自己的输出作为它自己的输入,尽管对于单个神经元来说有点奇怪,但是当几个神经元串在一起的时候,它们形成环路几乎是不可避免的。在不考虑抑制性输入stop的情况下,下方的神经元每隔一个时钟单元,就会输出1,将这个输出连接到上方的神经元的时候,最终的Output看起来就好像延时了两个时间单元一样。由于存在环路,这个过程将会一直循环下去,我们必须通过引入一个抑制性输入Stop,让它作为整个过程的开关去控制一切。你可以在下方阈值为1的神经元上再增加一个神经元从而让整个输出延迟三个时间单元。
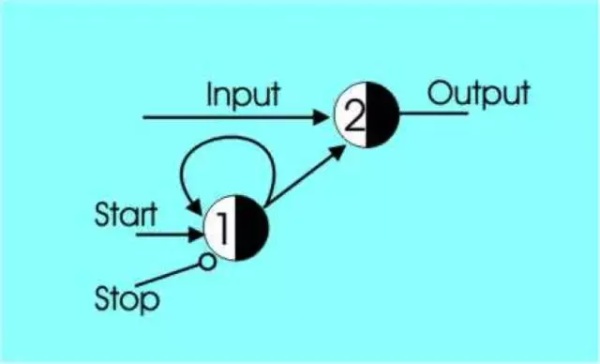
图3 带有回路的神经网络[4]
这种延时很重要,延时t时刻,意味着在这个信号可以在逻辑门中存储t时刻,这实际上意味着神经元具有了记忆功能。这种结构其实就是现在的寄存器的原型。类似的神经网络可以实现更复杂一点的电路,例如下图的神经元网络就实现了一个二分频电路,即在时钟每触发2个周期时,电路输出1个周期信号。
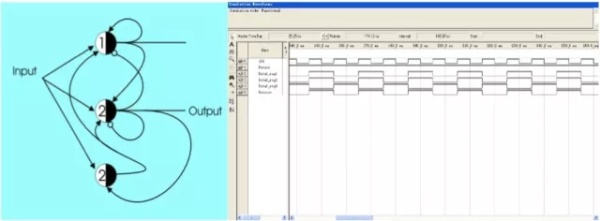
(a) (b)
图4 (a)二分频神经网络[4]及其(b)波形仿真
需要特别感谢我的同事为我绘制了这个波形仿真图。
以上的这些都来自于麦卡洛克和皮茨在1943年合著的那篇A Logical Calculus of the Ideas Immanent in Nervous Activity [6]即《神经活动中内在意识的逻辑演算》,简称《逻辑演算》,任性的是,这篇文章注明的参考文献只有卡尔纳普的《语言的逻辑句法》(皮茨据说也是很快就看完并做了大量笔记,这让卡尔纳普印象深刻)、希尔伯特和阿克曼的《数理逻辑原理》,以及怀特海和罗素的《数学原理》,但是论文中他们却说:“图灵机能够计算的数也能够被这样的网络所计算……这就从心理学的角度,论证了图灵关于可计算性的定义”,很明显,1936年阿兰图灵发表的创世之作《On Computable Numbers, with an Application to the Entscheidungsproblem》(论数字计算在决断难题中的应用)一定也对麦卡洛克产生了影响,更从一个角度反映出图灵是多么伟大,他几乎是从纯数学的角度出发,构思出一种将计算和自动化联系起来的机器,后人称之为“图灵机”。实际上,直到20世纪之前,人们普遍认为,所有的问题类都是有算法的就像我们在本文第一季看到的求解根号2[7]一样,人们的计算研究就是找出算法来。然而,20世纪初的时候,许多问题已经过长期研究仍然找不到算法,即它们是不可计算的。尽管有很多人(哥德尔,丘奇)已经表明了凡“算法可计算函数都是一般递归函数”(你可以不用理解它),但是图灵创造性的把计算归结为最简单、最基本、最确定的机械动作,执行这些机械动作的机器就是图灵机,并得出结论:“那些算法可计算的问题就是这种自动机能计算的问题”。遗憾的是,我们现在仍然不能区分哪些问题是可计算的,哪些问题是不可计算的。但是将计算和自动化机器联系起来的思想使得图灵被公认为“计算机科学之父”。然而,由于图灵机本身只是一个构想,麦卡洛克和皮茨的工作验证了通过神经元表示的逻辑门实现计算是一条切实可行的方法。这个方法为被称为“计算机之父”的冯诺伊曼去实现真正意义上的计算机提供了几乎唯一可以借鉴的思路。
在我们所学的大学计算机文化基础课程中,唯一让你印象深刻的可能就是“第一台通用计算机ENIAC是由宾西法尼亚大学发明的“,发明人莫克利(JohnW.Mauchly)和艾克特(J.PresperEckert)估计你也记不起来。这台机器更具有象征意义,它跟我们现在的计算机,差别很大,它竟然采用了十进制进行计算,而且每次计算不同的问题,需要几个操作员花几周的时间重新连接电线和开关!1945年6月,冯诺依曼撰写了一份历史性文件《EDVAC报告书的第一份草案》(First Draft of a Report on the EDVAC),这是第一份公开发表的关于存储程序概念的二进制计算机器——现代计算机。他建议计算机应该以皮茨和麦卡洛克的神经网络为模型,并且用真空电子管代替神经元作为逻辑门,这些逻辑门按照神经网络的方式组织起来就可以进行任何计算了。更为关键的是,为了使得程序本身能够像输入的数据一样保存起来(避免重新连接线路),他还建议计算机必须有另外一样新东西:内存,他说:需要一种「一个自激发元素将保持这种激发状态」的结构,其实这就是皮茨和麦卡洛克论文中出现的神经元构成的回路所产生的作用:记忆。这篇奠定了到目前为止所有计算机逻辑结构的EDVAC报告只有一篇参考文献:麦卡洛克和皮茨的《逻辑演算》。
在《逻辑演算》的原始论文中,延时门,或门和与门分别表示为下图的(a)(b)(c)。这个图据说是麦卡洛克的女儿绘制的[3]。
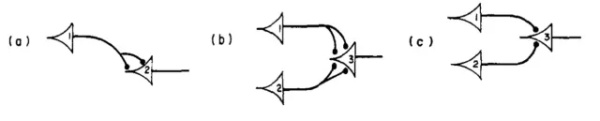
图 5 《逻辑演算》中的逻辑门[6]
我们大多数学习计算机的人,老师总会教导我们计算机本身就是0,1构成的,不管软件还是硬件,但是大家(特别是有软件工程背景的人)经常忽略的是在计算机中,时序电路的引进,才使得存储程序这一设计能够实现。
1943年,莱特文将皮茨带到了维纳在MIT的办公室,简单的交流就使得这位控制论的创始人认为皮茨「毫无疑问是我见过的最厉害的科学家。」[1]对于皮茨这个连高中都没有毕业的流浪儿来说,维纳承诺给予皮茨MIT的数学博士学位,并邀请皮茨到MIT与他一起工作。就算在那个被称之为“控制论学家“的圈子里面(维纳,冯诺依曼,麦卡洛克、莱特文),皮茨也是他们中的天才。维纳让皮茨继续改进他的神经网络,皮茨怀疑对于一个初始的随机的神经网络而言,”随着长时间对神经元阙值的调整,这种随机性会渐渐让位于有序性,而信息就涌现出来了“[1]。他着手用统计力学来为这个过程建模。维纳激动地鼓励他,他知道如果将这样一个模型植入一台机器的话,它就将能够「学习」[1]。这段描述简直就是现在深度学习所做的一切。但是对神经元的调整这件事当时还不能自动进行,这件事还必须等到1957年感知机出现的时候。实际上,为了更加清楚地了解这一点,麦卡洛克和皮茨的神经元模型还可以被描述成下面的图形:
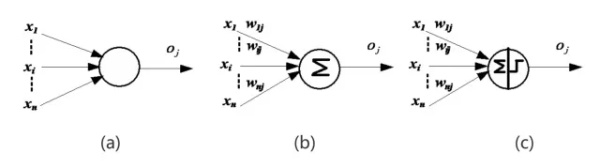
图6 神经元的结构图
这种表示与现在神经网络中的表示几乎没什么差别了,图(a)表示神经元从外界获得输入

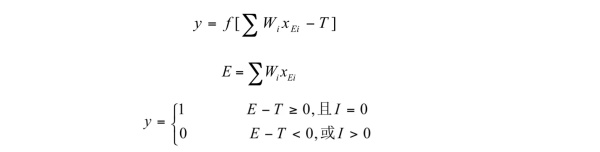
其中,y表示神经元的输出,E表示神经元获得外界刺激的和,T表示神经元设定的阈值,I表示抑制性突触,它起到的作用就是图2中非门的那个控制信号。当我们精心挑选权值参数W,阈值T,以及控制信号I的话,就能让神经元实现逻辑运算了,例如:
设T=2,I=0,W1=1,W2=1,
那么 E=x1W1+x2W2=x1+x2
当x1=1,x2=1,E=1+1=2, 触发y=1
当x1=1,x2=0,E=1+0=1, 不触发y=0
当x1=0,x2=1,E=0+1=1, 不触发y=0
当x1=0,x2=0,E=0+0=0, 不触发y=0
这就实际上实现了x1和x2之间的“逻辑与“运算。
这个模型看起来威力无穷,但是一个最关键的问题是必须依靠人去精心设计参数的值以完成某项计算功能,自动化的过程并不彻底。如果神经网络的结构和参数都能根据不同的任务自动确定,这样构建的机器被认为具有学习功能。然而,如何仅仅自动化的选择参数,使得单个神经元具有学习能力一直到 罗森布拉特的感知机才提出解决办法,我们已经知道,这个办法跟求解根号2几乎没区别,但是感知机的重要性是不言而喻的。如果能够自适应地组建神经网络的结构,人工智能可能将取得大进展。实际上,由于网络本身就是一个带权的图,图理论与神经网络的结合几乎是不可避免的事情,特别是包含逻辑推理关系(知识)的图模型与神经网络的结合更加吸引人。在最近的一个报告中[8], 27位学者(其中22位来自AlphaGo的东家DeepMind),对这种可能性进行了阐述。沿这个方向继续下去并取得重大成果的话,可能将为人工智能开创一个比现如今的深度学习更加完善的基础。
现在还是回到历史中,我们需要花点时间总结一下麦卡洛克和皮茨发明的神经计算模型的历史地位了。这个现在被称之为MP模型(McCulloch-Pitts Model)的东西被现代的人们忽略了,它最少在三个方面产生了重要影响:首先,将生理学关于神经的研究进展带入到数学领域,并与逻辑学相结合,直到现在,也有很多人认为,为了使机器具有智能必须回归对神经科学或者大脑的研究,麦卡洛克和皮茨绝对是这个领域的第一人。另外,你可以坚定的认为MP模型催生了现代计算机科学的诞生,并使得这个科学从一开始就分成两个部分,一部分借鉴他们的由神经元构成的神经网络实现逻辑计算,同时也为存储程序设计带了最原始的参考,MP模型为图灵机和现代的存储程序计算机之间建立了一个至关重要的桥梁,为后来复杂的计算机硬件体系结构带来了最初的灵感。另一方面,由于这个神经网络的参数无法实现真正的学习,从皮茨开始,就有一些研究者开始致力于让神经网络自动学习,它构成了当前机器学习或人工智能研究的半壁江山(谦虚地说)。当前,在很多机器学习课上,老师们都会强调机器学习的编程范式与传统的基于过程的编程完全不一样,实际上,就是从皮茨开始,就注定了两者完全不在一个层次上。传统的计算机硬件或软件编程大都还是与MP方法一样,需要人为地设置参数或者可能的情况,机器学习则不太一样,它他希望机器能像人一样,从环境的刺激(数据)中学习一个模型来应对环境的刺激,这个模型最早的例子就是感知机。通过这些资料的学习和整理,我逐渐清晰地看到, MP模型和感知机实际上代表了计算机科学发展的两条不同路径。以MP为背景的计算机体系强调计算与存储(记忆),以感知机为开端的思想则强调学习。
故事进入尾声,控制论的创始人,性格怪异不讨人(罗素,香农等)喜欢的维纳成就了皮茨,但是维纳的性格预示着皮茨在他身边也是危险的,更别说维纳身边有一个纳粹背景的妻子。玛格丽特·维纳从各方面讲都是一个有控制欲的、保守的假正经。由于后来一个偶然的机会,麦卡洛克也来到MIT和皮茨一起在维纳手下工作。突然有一天,维纳告诉麦卡洛克,皮茨和莱特文:“所有我和你们项目之间的联系被永久性的解除了“。此后他再也没有同皮茨说过话,也不告诉他为什么。一种说法是[2,3]玛格丽特受不了麦卡洛克疯子般的自由生活习惯(麦卡洛克会写诗,并到处炫耀),造谣说麦卡洛克手下的几个男孩勾引了维纳的宝贝女儿。还有一种说法[3]是”精神有缺陷的维纳已经无法捕捉麦卡洛克言语表达中的细微差别。有些时候,维纳分辨不出麦卡洛克是在陈述一件事实还是在说一个猜想”。维纳和麦卡洛克以及皮茨突然地决裂对控制论遭受很大损失,皮茨则遭受了最大的打击,几乎完全垮掉,他开始酗酒,甚至自己合成类似鸦片的化学物质作为下酒菜,他毁掉了他的研究成果和博士论文,拒绝接受任何帮助。在给麦卡洛克写下一封”这一切都让我感到极度悲哀”的信[1]不久,1969年5月14日,沃尔特·皮茨在剑桥的寄宿之家孤独死去,死因是长期酗酒导致的肝硬化出血。这个从小就开始流浪的大男孩一生没有得到过任何一个正式的文凭,但是他依然不愧是计算科学史上一颗耀眼的明星。四个月后,麦卡洛克也过世了。能让我们感到欣慰的是,从小孤苦伶仃的皮茨一生中能遇到麦卡洛克,他也是幸运的。皮茨从麦卡洛克那里得到了他需要的一切:”认同、友谊、「智识」上的另一半以及他从未有过的父爱” [1]。
麦卡洛克和皮茨实际上为控制论带来了最有力的证据,也为维纳带去了信心。控制论的核心思想几乎可以在麦卡洛克和皮茨的工作中体现。第一,控制,指的是系统能够与环境交互继而改变环境的能力,实际上任何一种能够接收环境数据,并进行输出的东西,都可称之为控制,神经元或神经网络就是典型代表。第二,反馈,指的是能够使用过去的性能来调整未来行为的一种属性,在神经元上,环状的链接,就是一种反馈,甚至你可以回到我们在本文第1季的求解根号的流程[7],用错误反馈给系统,以指导下一步计算的结果。控制论的目标实在太过宏大,当时对很多学科产生了非常重要的影响,然而现在这种影响力正在减退。遗憾的是,为维纳《控制论》思想贡献巨大的麦卡洛克和皮茨甚至都没能出现在维纳的自传里,想想作者是维纳,你应该可以理解。现在,麦卡洛克和皮茨也被后人称为控制论学家,这对维纳来说,实在是有点讽刺。甚至是最新的一本关于控制论历史的科普读物《机器崛起:遗失的控制论历史》[5]中竟然连皮茨都没有提到,不知道维纳是否于心有愧,他肯定不知道“原来随便错手,可毁了人一世”。
神经元模型的创立者皮茨是不幸的,遗憾的是,感知机的发明人弗兰克· 罗森布拉特(Frank Rosenblatt)也几乎一样不幸。
参考文献
[1] 陨落的天才-皮茨和他违背的逻辑,人工智能名人堂第25期
[2] 尼克,人工智能简史 人民邮电出版社,2017.12.
[3] Charles Petzold,图灵的秘密:他的生平、思想及论文解读 杨卫东 , 朱皓 (译者)
[4] Harry Fairhead, The McCulloch-Pitts Neuron, https://www.i-programmer.info/ babbages-bag/325-mcculloch-pitts-neural-networks.html
[5] 期马斯·瑞德 , 机器崛起:遗失的控制论历史, 机械工业出版社,2017
[6] Pitts, Walter. A logical calculus of the ideas immanent in nervous activity. Neurocomputing: foundations of research. MIT Press, 1988:115-133.
[7] twinlj77,理解计算:从√2到AlphaGo ——第1季 从√2谈起, https://blog.csdn.net/SIGAI_CSDN/article/details/80886538
[8] Peter W. Battaglia, J
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/%E4%BA%92%E8%81%94%E7%BD%91/%E7%90%86%E8%A7%A3%E8%AE%A1%E7%AE%97%E4%BB%8E%E6%A0%B9%E5%8F%B7%E5%88%B0%E7%AC%AC%E5%AD%A3%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C%E7%9A%84%E6%95%B0%E5%AD%A6%E6%A8%A1%E5%9E%8B/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


