电商搜索场景中的强化排序学习形式化理论分析以及应用
在淘宝的商品搜索场景中,给商品进行打分排序是一个典型的多步决策问题。尽管 Learning to Rank(LTR)被广泛用于排序问题,但现有的方法并没有考虑同一个搜索会话中不同决策步骤之间的关联性,因而无法直接用于电商搜索场景中的商品排序。本文提出用强化学习来解决对商品多步排序决策问题,它在模拟实验及淘宝搜索场景中有非常好的效果。实验证明,本论文提出的算法在多步排序问题中的性能要高于现有的Online LTR方法。
本文主要贡献如下:
(1)对电商搜索场景中的多步排序问题进行形式化描述,定义搜索会话马尔科夫决策过程问题模型(Search Session Markov Decision Process, SSMDP);
(2)从理论上分析 SSMDP 的性质,并证明累积奖赏最大化对于多步排序问题的必要性;
(3)提出全新的策略梯度算法 Deterministic Policy Gradient with Full Backup Estimation(DPG-FBE),解决了 SSMDP 中奖赏值方差较大以及奖赏分布高度不平衡的问题。
一、背景
在任何一个电商平台中(如:淘宝、亚马逊等),商品搜索都是一项基础性的服务。用户通过商品搜索引擎对目标商品进行搜索、浏览、比较,进而选取自己满意的商品购买。本文关注商品搜索场景中对商品进行打分排序的问题。具体地,商品排序问题可以从一个搜索会话中用户与搜索引擎之间交互的角度来进行描述:(1)用户进入搜索引擎,输入 query;(2)对候选商品进行打分排序,并从中选取分数最高的前 K(比如:K=10)个商品进行展示;(3)用户在商品展示页面上进行浏览、点击、购买、翻页等操作;(4)当用户选择翻页时,搜索引擎将对未展示商品进行重新排序,然后又展示分数最高的前 个商品;(5)这一过程将持续进行下去直到用户退出搜索会话(比如:发生购买或者放弃搜索)。
用户在搜索会话中的操作(比如:点击商品)是反映用户对商品偏好的信号。从统计的角度来看,这些信号可以用来学习排序打分函数,使得用户更喜爱的商品(比如:点击率更高的商品)能够有更高的排序分数或次序。Learning to Rank(LTR)方法正是基于这样的思想而提出。早期基于监督学习的 LTR 方法大致可以分为 Point-wise LTR、Pair-wise LTR 以及 List-wise LTR。最近十多年,在线学习的理论模型和技术也被很多研究者将引入到 Learning to Rank 领域中,使得一系列 Online LTR 方法被相继提出,如:BatchRank [1]、 CascadeKL-UCB [2]、RankedExp3 [3] 等。
尽管 LTR 研究领域蓬勃发展,但现有的 LTR 方法基本上都无法直接用于电商搜索场景中的商品排序问题。其原因在于,同一个搜索会话中的不同排序决策之间是存在一定相关性的。举一个直观的例子,用户在一页一页浏览商品时,看过的商品必然会对用户如何看待后续页面上的商品产生影响。然而,现有的 LTR 方法并没有考虑这种相关性,对每一个排序决策步骤均独立看待。为了利用这种同一搜索会话中不同排序决策步骤之间的相关性,本文提出将强化学习(Reinforcement Learning)应用于商品排序问题中,并考查最大化累积奖赏这种机制在其中的具体作用。本文接下来的内容包括对商品排序问题的形式化建模、理论分析、新型算法设计以及实验结果。
二、搜索排序问题形式化
如前所述,在淘宝、天猫等电商平台的商品搜索场景中,对商品的打分排序是一个多步顺序决策问题。本节将提出搜索会话马尔科夫决策过程模型(Search Session Markov Decision Process, SSMDP),作为对搜索排序问题的形式化定义。在此之前,我们通过手机淘宝中具体的例子复述用户和搜索引擎之间的会话过程,加强直观感受。
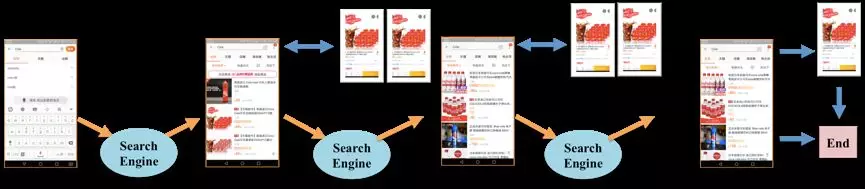
图 1. 手机淘宝中搜索会话示意图
如图所示,用户和搜索引擎之间的搜索会话过程为:
(1)用户在手机淘宝的搜索框中输入「可乐」作为 query,并点击「搜索」按钮。 (2)搜索引擎执行一次商品排序,并展示第一个可乐商品页面。
(3)用户浏览第一个商品展示页,并点击其中某些商品进入详情页。
(4)用户发现并没有满意的商品,于是向下滑动手机屏幕,提出翻页请求。
(5)搜索引擎接到翻页请求,执行第二次商品排序,并展示第二个可乐商品页面。 (6)经过若干次这样的「翻页-排序-浏览」回合,搜索会话将最终在用户购买某个可乐商品或者放弃浏览时结束。
2.1 搜索排序问题建模
我们首先对搜索会话过程中的上下文信息和用户行为进行建模,定义商品页、商品页历史、成交转化率等概念,它们是定义状态和状态转移关系的基础。
定义 1. [Top K List]
给定商品集合 D,排序函数 f,以及一个正整数
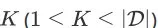 ,关于 D 和 f 的 top K list,记为
,关于 D 和 f 的 top K list,记为
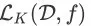 ,是用函数f对 D 中商品进行打分以后的前 K 个商品的有序列表
,是用函数f对 D 中商品进行打分以后的前 K 个商品的有序列表
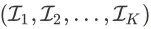 。其中,
。其中,
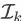 是排在第 k 位的商品(
是排在第 k 位的商品(
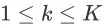 ),并且对于任意
),并且对于任意
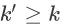 ,都有
,都有
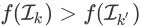 。
。
定义 2. [Item Page]
令 D 为关于某个 query 的商品全集,
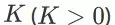 为一个页面能够展示的商品数量。对于一个搜索会话的任意时间步 t (
为一个页面能够展示的商品数量。对于一个搜索会话的任意时间步 t (
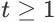 ),其对应的 item page
),其对应的 item page
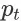 是关于的第(t-1)步的打分函数
是关于的第(t-1)步的打分函数
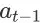 和未展示商品集合
和未展示商品集合
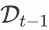 的 top K list
的 top K list
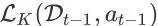 。对于初始时间步 t = 0,有
。对于初始时间步 t = 0,有
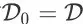 。对于其他任意时间步
。对于其他任意时间步
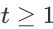 ,有
,有
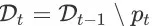 。
。
定义 3. [Item Page History]
令 q 为一个搜索会话的 query。对于初始时间步 t = 0,对应的初始 item page history 为
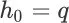 。对于任意其他时间步
。对于任意其他时间步
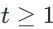 ,对应的 item page history 为
,对应的 item page history 为
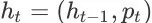 。在这里,
。在这里,
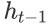 为第(t - 1)步的 item page history,
为第(t - 1)步的 item page history,
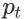 为第 t 步的 item page。
为第 t 步的 item page。
对于任意时间步骤 t,item page history
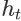 包含了用户在 t 时刻能够观察到的所有上下文信息。由于商品全集 D 是一个有限集合,不难发现一个搜索会话最多包含
包含了用户在 t 时刻能够观察到的所有上下文信息。由于商品全集 D 是一个有限集合,不难发现一个搜索会话最多包含
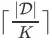 个 item page。对于搜索引擎来讲,它在一个搜索会话中最多决策
个 item page。对于搜索引擎来讲,它在一个搜索会话中最多决策
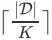 次。根据我们之前的数据分析,不同的用户会在不同的时间步上选择购买或者离开。如果我们把所有用户看作一个能够采样出不同用户行为的 environment,就意味着这个 environment 可能会在任意时间步上以一定的成交转化概率(conversion probability)或者放弃概率(abandon probability)来终止一个搜索会话。我们形式化定义这两种概率如下。
次。根据我们之前的数据分析,不同的用户会在不同的时间步上选择购买或者离开。如果我们把所有用户看作一个能够采样出不同用户行为的 environment,就意味着这个 environment 可能会在任意时间步上以一定的成交转化概率(conversion probability)或者放弃概率(abandon probability)来终止一个搜索会话。我们形式化定义这两种概率如下。
定义 4. [Conversion Probability]
对于一个搜索会话中的任意 item page history
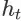 ( t > 0 ),令
( t > 0 ),令
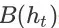 表示用户在观察到
表示用户在观察到
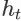 之后发生购买行为的随机事件,则
之后发生购买行为的随机事件,则
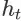 的 conversion probability,记为
的 conversion probability,记为
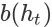 ,就是事件
,就是事件
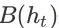 在
在
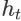 下发生的概率。
下发生的概率。
定义 5. [Abandon Probability]
对于一个搜索会话中的任意 item page history
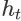 ( t > 0 ),令
( t > 0 ),令
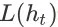 表示用户在观察到
表示用户在观察到
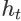 之后离开搜索会话的随机事件,则
之后离开搜索会话的随机事件,则
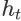 的 abandon probability,记为
的 abandon probability,记为
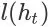 ,就是事件
,就是事件
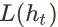 在
在
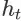 下发生的概率。
下发生的概率。
由于
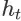 是在(t - 1)时刻的 item page history
是在(t - 1)时刻的 item page history
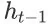 上执行动作
上执行动作
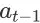 的直接结果,因此
的直接结果,因此
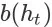 和
和
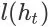 也表征了 Agent 在
也表征了 Agent 在
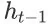 上执行动作
上执行动作
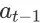 之后环境状态的转移:(1)以
之后环境状态的转移:(1)以
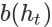 的成交概率终止搜索会话;(2)以
的成交概率终止搜索会话;(2)以
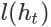 的离开概率终止搜索会话;(3)以
的离开概率终止搜索会话;(3)以
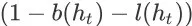 的概率继续搜索会话。方便起见,我们对用户继续进行搜索会话对概率也进行形式化描述。
的概率继续搜索会话。方便起见,我们对用户继续进行搜索会话对概率也进行形式化描述。
定义 6. [Continuing Probability]
对于一个搜索会话中的任意 item page history
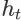 ( t > 0 ),令
( t > 0 ),令
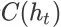 表示用户在观察到
表示用户在观察到
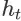 之后继续停留在会话中的随机事件,则
之后继续停留在会话中的随机事件,则
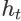 的 continuing probability,记为
的 continuing probability,记为
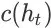 ,就是事件
,就是事件
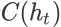 在
在
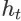 下发生的概率。
下发生的概率。
显然,对于任意 item page history h,都有
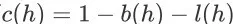 成立。特殊地,对于初始 item page history
成立。特殊地,对于初始 item page history
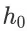 来讲,
来讲,
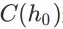 是一个必然事件(即
是一个必然事件(即
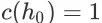 )。这是因为在第一个 item page 展示给用户前,不可能存在成交转化事件和离开事件。
)。这是因为在第一个 item page 展示给用户前,不可能存在成交转化事件和离开事件。
2.2 搜索会话马尔科夫决策过程
基于上面定义的几个概念,我们可以定义 search session MDP(SSMDP)如下:
定义 7. [Search Session MDP]
令 q 为某个 query,D 为和 q 相关的商品全集,K 为一个页面可展示的商品数量,关于 q、D 和 K 的 search session MDP 是一个元组,记为
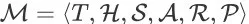 。该元组中的每个要素分别为:
。该元组中的每个要素分别为:
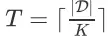 为搜索会话最大决策步数,
为搜索会话最大决策步数,
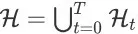 为关于 q 、D 和 K 的所有可能的 item page history 的集合,其中
为关于 q 、D 和 K 的所有可能的 item page history 的集合,其中
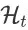 为 t 时刻所有可能 item page history 的集合
为 t 时刻所有可能 item page history 的集合
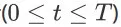 ,
,
 为状态空间,
为状态空间,
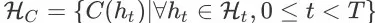 是包含所有的继续会话事件的非终止状态集合(nonterminal state set),
是包含所有的继续会话事件的非终止状态集合(nonterminal state set),
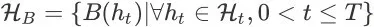 和
和
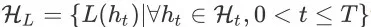 分别是包含所有成交转化事件和离开事件的终止状态集合(terminal state set),
分别是包含所有成交转化事件和离开事件的终止状态集合(terminal state set),
-
A 为动作空间,包含搜索引擎所有可能的排序打分函数,
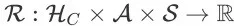 为奖赏函数,
为奖赏函数,
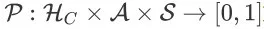 为状态转移函数,对于任意时间步
为状态转移函数,对于任意时间步
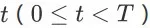 、任意 item page history
、任意 item page history
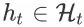 和任意动作
和任意动作
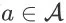 ,令
,令
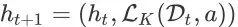 ,则 agent 在状态
,则 agent 在状态
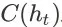 上执行动作 a 后,环境转移到任意状态
上执行动作 a 后,环境转移到任意状态
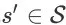 的概率为
的概率为
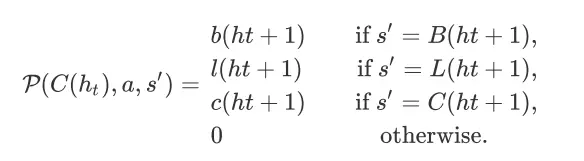
在一个 Search Session MDP 中,Agent 是搜索引擎,环境是所有可能用户共同构成的总体。环境的状态表征了用户总体在对应 item page history 下的动向(继续会话、成交或离开)。动作空间 可以根据任务需要进行设定(例如:离散的动作空间或连续的动作空间)。环境状态的转移则直接基于我们之前定义的成交转化概率(conversion probability)、放弃概率(abandon probability)以及继续会话概率(continuation probability)。奖赏函数与具体的任务目标高度相关,我们将在下一节进行讨论。
2.3 奖赏函数
在一个 Search Session MDP
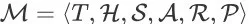 中,奖赏函数 R 是对每个状态下的每个动作的即时效用的量化评估。具体地,对于任意的非终止状态
中,奖赏函数 R 是对每个状态下的每个动作的即时效用的量化评估。具体地,对于任意的非终止状态
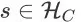 ,任意动作
,任意动作
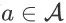 ,以及任意其他状态
,以及任意其他状态
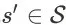 ,
,
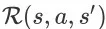 表示在状态 s 中采取动作 a,并且环境状态转移到 s’ 的情况下,Agent 从环境获得的即时奖赏期望。因此,在搜索排序问题中,我们必须将用户在每个商品展示页面的反馈信息(翻页、点击、购买等)转化为学习算法能够理解的奖赏值。
表示在状态 s 中采取动作 a,并且环境状态转移到 s’ 的情况下,Agent 从环境获得的即时奖赏期望。因此,在搜索排序问题中,我们必须将用户在每个商品展示页面的反馈信息(翻页、点击、购买等)转化为学习算法能够理解的奖赏值。
在 online LTR 研究领域,用户的点击反馈被广泛用作定义奖赏值的基础 [1,4,5]。然而,在电商场景中,买家和卖家之间的成功交易要比用户点击更加重要。基于阿里巴巴让天下没有难做的生意的使命,也就是,我们定义的奖赏函数将尽可能多地促进用户与卖家之间的交易。对于任意时间步
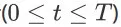 、任意 item page history
、任意 item page history
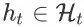 和任意动作
和任意动作
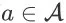 ,令
,令
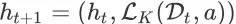 。在观察到 item page history
。在观察到 item page history
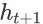 ,用户将以
,用户将以
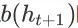 的平均概率购买商品。尽管不同的用户会选择不同的商品进行购买,但从统计的角度来看,在
的平均概率购买商品。尽管不同的用户会选择不同的商品进行购买,但从统计的角度来看,在
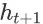 上发生的成交转化事件对应的商品成交价格必然会服从一个特定的分布。我们用
上发生的成交转化事件对应的商品成交价格必然会服从一个特定的分布。我们用
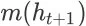 表示 item page history
表示 item page history
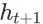 的成交价格期望,则 agent在状态
的成交价格期望,则 agent在状态
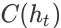 上执行动作 a 并且环境转移到任意状态
上执行动作 a 并且环境转移到任意状态
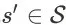 的奖赏定义如下:
的奖赏定义如下:
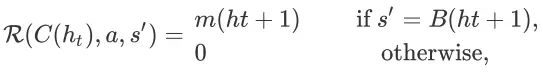
在这里,
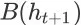 为
为
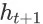 上发生的成交转化事件对应的终止状态。从我们的奖赏函数定义可以看到,Agent 只有在成交发生时才能从环境获得正的奖赏。在其他情况下,Agent 获得的奖赏值都是零。需注意,任意 item page history 的成交价格期望通常是未知的。在具体应用中,我们可以用每一次的实际成交价格作为对应成交事件的奖赏信号。
上发生的成交转化事件对应的终止状态。从我们的奖赏函数定义可以看到,Agent 只有在成交发生时才能从环境获得正的奖赏。在其他情况下,Agent 获得的奖赏值都是零。需注意,任意 item page history 的成交价格期望通常是未知的。在具体应用中,我们可以用每一次的实际成交价格作为对应成交事件的奖赏信号。
三、理论分析
在将 Search Session MDP 模型进行实际应用之前,我们需要对一些细节做出说明。本节将首先证明 Search Session MDP 的状态具有马尔可夫性质,以证明该理论模型是良定义的。然后我们将在上一节给出的奖赏函数的基础上对折扣率进行理论分析,证明在搜索排序问题中最大化长期累积奖赏的必要性。
3.1 马尔可夫性质
上一节定义的 search session MDP(SSMDP)可以看作是 MDP 模型的一个实例,但要保证 SSMDP 是良定义的,我们需要证明 SSMDP 中的状态都具有马尔可夫性质(Markov Property)。马尔可夫性质指的是对于任意的状态动作序列
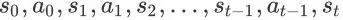 ,都有如下等式成立:
,都有如下等式成立:
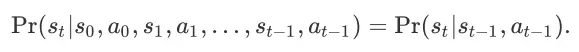
也就是说,当前状态 的发生概率仅仅取决于最近一个状态动作对
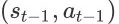 ,而并非整个序列。我们可以证明对于一个 SSMDP,它的所有状态都具有马尔可夫性质。
,而并非整个序列。我们可以证明对于一个 SSMDP,它的所有状态都具有马尔可夫性质。
命题 1
对于任意 search session MDP
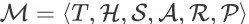 ,其状态空间 S 中的任意状态都具有马尔可夫性质。
,其状态空间 S 中的任意状态都具有马尔可夫性质。
证明:
我们只需证明对于任意时间步
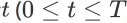 和关于 t 的任意状态动作序列
和关于 t 的任意状态动作序列
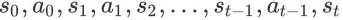 ,都有等式
,都有等式
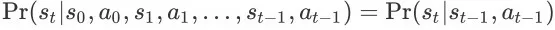 成立即可。
成立即可。
除了状态
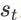 以外,序列
以外,序列
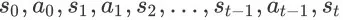 中的其他所有状态都是非终止状态(non-terminal state)。根据状态的定义,对于任意时间步
中的其他所有状态都是非终止状态(non-terminal state)。根据状态的定义,对于任意时间步
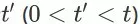 ,必然存在一个 item page history
,必然存在一个 item page history
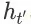 与状态
与状态
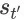 相对应,且有
相对应,且有
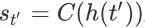 。因此,整个序列可以重写为
。因此,整个序列可以重写为
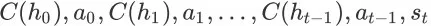 。需注意的是,对于任意时间步
。需注意的是,对于任意时间步
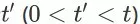 ,都有
,都有
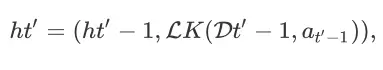
成立。其中,
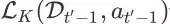 也就是关于
也就是关于
 时刻的动作
时刻的动作
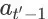 和未展示商品
和未展示商品
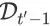 的 top K list。给定
的 top K list。给定
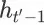 ,集合
,集合
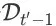 一定是确定的。所以,
一定是确定的。所以,
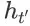 也就是状态动作对
也就是状态动作对
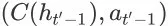 的必然和唯一结果。那么事件
的必然和唯一结果。那么事件
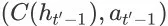 也就能够等价地表示为事件
也就能够等价地表示为事件
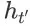 。基于此,我们可以进行如下推导:
。基于此,我们可以进行如下推导:
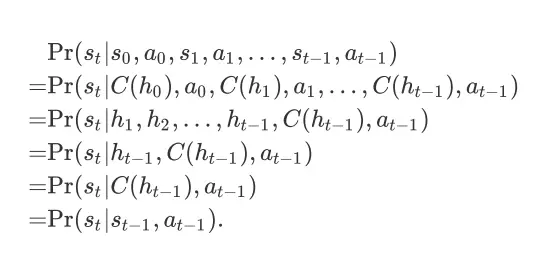
第三步推导成立是由于对于任意时间步
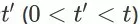 ,
,
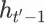 都包含在
都包含在
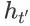 中。类似地,第四步推导成立是由于事件
中。类似地,第四步推导成立是由于事件
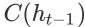 已经包含了
已经包含了
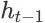 的发生。
的发生。
3.2 折扣率
在这一小节我们将讨论本文最重要的问题:延迟奖赏(delay reward)对于搜索排序的优化到底有没有作用?简单地来说,也就是 search session MDP 的折扣率(discount rate)到底应该设多大。在任意 MDP 中,折扣率 y 的大小直接决定了 future rewards 在 agent 的优化目标中所占比重。我们将分析优化长期累积奖赏与优化搜索引擎的经济指标这两个目标之间的关系给出答案。
令
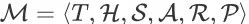 为一个关于 query q、商品全集 D 和正整数 K ( K > 0 ) 的 SSMDP。给定一个确定性策略
为一个关于 query q、商品全集 D 和正整数 K ( K > 0 ) 的 SSMDP。给定一个确定性策略
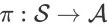 ,记每个时间步
,记每个时间步
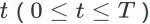
对应的 item page history 为
 ,我们把在策略
,我们把在策略
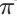 下能够访问的所有状态都展示在图 2 中。
下能够访问的所有状态都展示在图 2 中。
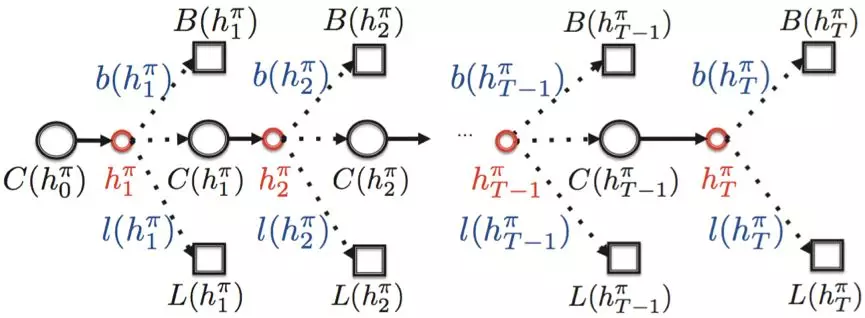
图 2. Search Session MDP 在固定策略 下能够访问的所有状态示意图
在这个图中,红色的节点表示 item page history,注意它们并不是 SSMDP 的状态。方便起见,在本文接下来的部分,我们将把
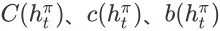 和
和
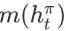
分别简化记为
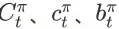 和
和
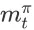 。
。
不失一般性,我们设 SSMDP
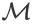 的折扣率为
的折扣率为
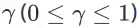 。由于 SSMDP 是一个有限时间步 MDP(finite-horizon MDP),所以折扣率可以取到 1。对于任意时间步
。由于 SSMDP 是一个有限时间步 MDP(finite-horizon MDP),所以折扣率可以取到 1。对于任意时间步
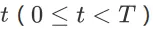 ,状态
,状态
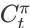 的 state value 为
的 state value 为
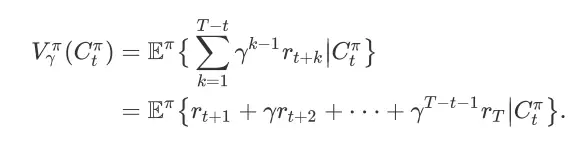
其中,对任意
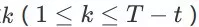 ,
,
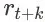 为 agent 在未来时刻 (t + k)的 item page history
为 agent 在未来时刻 (t + k)的 item page history
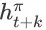 中收到的即时奖赏。根据我们奖赏函数的定义,
中收到的即时奖赏。根据我们奖赏函数的定义,
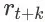 在策略
在策略
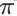 下的期望值为
下的期望值为
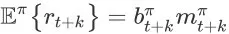 。在这里,
。在这里,
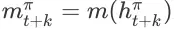 为 item page history
为 item page history
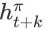 的成交价格期望。由于
的成交价格期望。由于
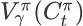 表达的是在
表达的是在
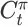 发生的条件下的长期累积奖赏期望,所以我们还要把从
发生的条件下的长期累积奖赏期望,所以我们还要把从
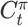 到达 item page history
到达 item page history
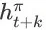 的概率考虑进来。记从状态
的概率考虑进来。记从状态
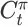 到达
到达
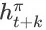 的概率为
的概率为
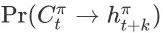 ,根据状态转移函数的定义可以得到
,根据状态转移函数的定义可以得到
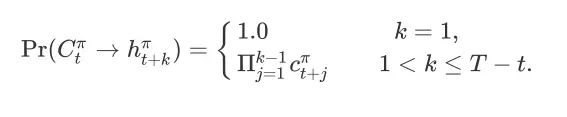
从状态
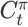 到 item page history
到 item page history
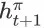 的概率为 1 是因为
的概率为 1 是因为
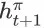 是状态动作对
是状态动作对
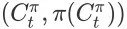 的直接结果。将上面的几个公式综合起来,我们可以进一步计算
的直接结果。将上面的几个公式综合起来,我们可以进一步计算
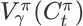 如下:
如下:
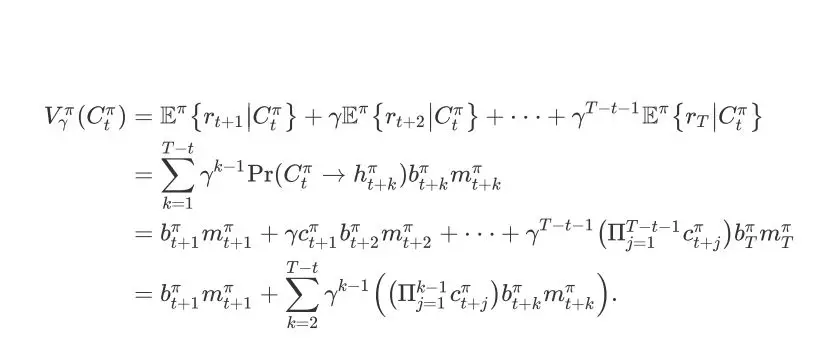
根据图 2 中展示的每个 item page history 的 conversion probability 以及成交价格期望,我们也可以将搜索引擎在策略
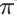 的作用下在一个搜索会话中引导的成交额期望表达出来,即
的作用下在一个搜索会话中引导的成交额期望表达出来,即
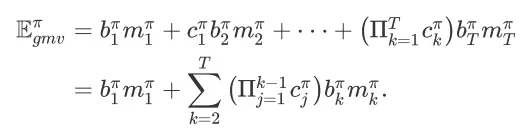
通过比较
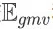 和
和
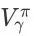 ,不难发现当折扣率 y = 1 时,有
,不难发现当折扣率 y = 1 时,有
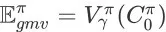 成立。也就是说,当 y = 1 时,最大化长期累积奖赏将直接带来搜索引擎成交额的最大化。当 y < 1 时,由于
成立。也就是说,当 y = 1 时,最大化长期累积奖赏将直接带来搜索引擎成交额的最大化。当 y < 1 时,由于
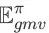 是
是
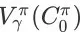 的上界,所以最大化
的上界,所以最大化
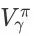 并不一定能够最大化
并不一定能够最大化
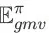 。
。
命题 2
令
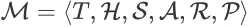 为任意 search session MDP。对于任意确定性策略
为任意 search session MDP。对于任意确定性策略
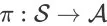 和折扣率
和折扣率
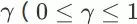 ,都有式子
,都有式子
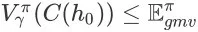 成立,其中
成立,其中
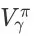 为 agent 在策略
为 agent 在策略
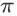 和折扣率 y 下的状态值函数,
和折扣率 y 下的状态值函数,
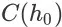 为搜索会话的初始状态,
为搜索会话的初始状态,
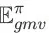 为搜索引擎在策略
为搜索引擎在策略
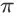 下的单次搜索会话成交额期望。并且仅当 y = 1 时,有
下的单次搜索会话成交额期望。并且仅当 y = 1 时,有
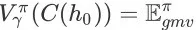 成立。
成立。
证明:
我们只需证明当 y < 1 时,有
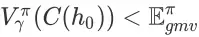 成立。这是显然的,因为二者之差,即
成立。这是显然的,因为二者之差,即
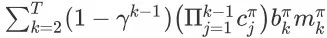 在 y < 1 时一定为正。
在 y < 1 时一定为正。
至此,我们可以回答之前提出的问题:站在提高搜索引擎成交额的角度,搜索排序问题中考虑延迟奖赏是必要且必须的。从理论上,这是因为最大化无折扣累积奖赏能够直接优化搜索引擎的成交额。究其深层原因,是因为用户在搜索商品的每个步骤(即每个 item page history)的行为都是基于之前观察到的所有信息(或者大部分信息)做出的反应,这天然决定了搜索排序问题的序列决策本质。
四、算法设计
本节将提出一个全新的策略梯度算法,用于学习 Search Session MDP 的最优排序策略。采用策略梯度算法能将排序策略用参数化的函数来表示,并直接对策略函数的参数进行优化。这能够同时解决 Search Session MDP 中排序策略的表示以及大规模状态空间的难题。我们首先在 Search Session MDP 的语境下对策略梯度方法进行简要回顾。另
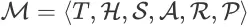 为一个 Search Session MDP,
为一个 Search Session MDP,
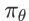 为参数化的排序策略函数,其参数为
为参数化的排序策略函数,其参数为
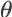 。Agent 的学习目标是找到最优的策略函数参数,使得它在所有可能状态-动作-奖赏轨迹中的
。Agent 的学习目标是找到最优的策略函数参数,使得它在所有可能状态-动作-奖赏轨迹中的
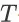 -步回报最大:
-步回报最大:
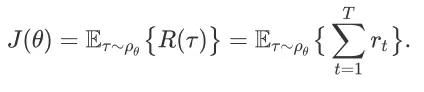
在这里,
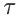 为形如
为形如
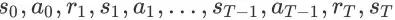 的状态-动作-奖赏轨迹,它服从策略参数为
的状态-动作-奖赏轨迹,它服从策略参数为
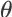 时的轨迹概率分布
时的轨迹概率分布
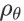 ;
;
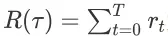 为轨迹
为轨迹
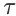 对应的
对应的
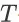 -步回报。需注意的是,如果在轨迹
-步回报。需注意的是,如果在轨迹
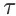 中到达终止状态的步数小于
中到达终止状态的步数小于
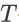 ,那么对应的奖赏和
,那么对应的奖赏和
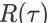 将在那个状态进行截断。优化目标
将在那个状态进行截断。优化目标
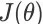 关于参数
关于参数
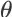 的梯度为
的梯度为
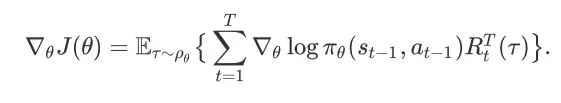
其中,
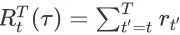 表示在轨迹
表示在轨迹
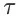 中,从时间步 t 到时间步
中,从时间步 t 到时间步
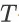 之间的奖赏之和。此梯度更新公式是著名的REINFORCE 算法 [6] 的核心。Sutton 等人提出的策略梯度定理(policy gradient theorem)[7] 提供了更加一般的策略梯度更新方法。一般地,
之间的奖赏之和。此梯度更新公式是著名的REINFORCE 算法 [6] 的核心。Sutton 等人提出的策略梯度定理(policy gradient theorem)[7] 提供了更加一般的策略梯度更新方法。一般地,
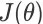 的梯度为
的梯度为
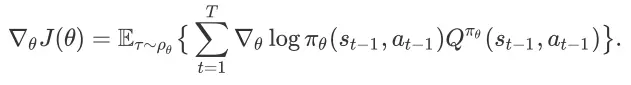
在这里,
 为策略
为策略
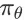 下的状态动作值函数。如果策略
下的状态动作值函数。如果策略
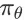 是一个确定性策略(deterministic policy),那么
是一个确定性策略(deterministic policy),那么
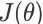 的梯度可以重写为
的梯度可以重写为
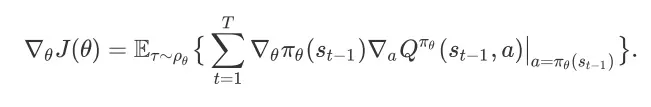
Silver 等人证明了确定性策略梯度(deterministic policy gradient)[8] 是一般性的随机策略梯度(stochastic policy gradient)在策略方差趋近于 0 时的极限。状态动作值函数
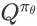 可以通过蒙特卡洛估值方法(Monte Carlo evaluation)或时间差分方法(temporal-difference learning)进行估计。例如,REINFORCE 算法采用的就是蒙特卡洛估值方法,而 Sutton 等人提出的演员评论家方法(actor-critic method)[9] 则采用的是时间差分方法对值函数进行估计。
可以通过蒙特卡洛估值方法(Monte Carlo evaluation)或时间差分方法(temporal-difference learning)进行估计。例如,REINFORCE 算法采用的就是蒙特卡洛估值方法,而 Sutton 等人提出的演员评论家方法(actor-critic method)[9] 则采用的是时间差分方法对值函数进行估计。
我们基于确定性策略梯度算法(deterministic policy gradient,DPG)[8] 提出学习 Search Session MDP 最优排序策略的算法。我们并没有基于更一般的随机策略梯度方法,因为计算随机策略的梯度通常需要更多样本,且这一点在高维动作空间问题中更为明显。然而,在 Search Session MDP 中,对状态动作值函数
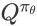 进行估计面临两个难点。首先,Agent 在每个状态上所能获得的即时奖赏具有很大的方差。从奖赏函数的定义可以看到,任意状态动作对(s, a)对应的即时奖赏要么为 0,要么为 (s, a)对应的 item page history 的成交价格期望 m(h),而 m(h)的值通常比 0 大很多。对
进行估计面临两个难点。首先,Agent 在每个状态上所能获得的即时奖赏具有很大的方差。从奖赏函数的定义可以看到,任意状态动作对(s, a)对应的即时奖赏要么为 0,要么为 (s, a)对应的 item page history 的成交价格期望 m(h),而 m(h)的值通常比 0 大很多。对
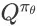 进行估计的第二个难点在于每个状态上的即时奖赏分布的高度不平衡。对于任意状态动作对(s, a),由(s, a)引导的成交转化事件(产生非零即时奖赏)发生的概率要远远低于由(s, a)引导的继续会话事件和离开事件(这两类事件产生值为 0 的即时奖赏)。不单是即时奖赏,Search Session MDP 中状态-动作-奖赏轨迹的-
进行估计的第二个难点在于每个状态上的即时奖赏分布的高度不平衡。对于任意状态动作对(s, a),由(s, a)引导的成交转化事件(产生非零即时奖赏)发生的概率要远远低于由(s, a)引导的继续会话事件和离开事件(这两类事件产生值为 0 的即时奖赏)。不单是即时奖赏,Search Session MDP 中状态-动作-奖赏轨迹的-
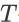 步回报也同样存在方差较高和分布不平衡的问题。这是因为在任何一条可能的状态-动作-奖赏轨迹中,只有最后一步的奖赏值可能为非零。因此,如果简单地采用蒙特卡洛估值方法或者时间差分方法来对 进行估计将会导致不精确的值函数更新,从而影响参数
步回报也同样存在方差较高和分布不平衡的问题。这是因为在任何一条可能的状态-动作-奖赏轨迹中,只有最后一步的奖赏值可能为非零。因此,如果简单地采用蒙特卡洛估值方法或者时间差分方法来对 进行估计将会导致不精确的值函数更新,从而影响参数
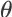 的优化。
的优化。
我们解决上述问题的方法类似于基于模型的强化学习方法 [10,11],借助对环境模型(奖赏函数和状态转移函数)的近似估计来完成可信的值函数更新。根据贝尔曼等式,任意状态动作对(s, a)在策略
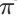 下的状态动作值为
下的状态动作值为
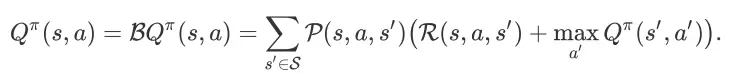
其中,
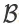 表示贝尔曼操作。令
表示贝尔曼操作。令
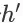 为(s, a)引导的 item page history。根据 Search Session MDP 的状态转移函数定义,在环境接收(s, a)之后,只有
为(s, a)引导的 item page history。根据 Search Session MDP 的状态转移函数定义,在环境接收(s, a)之后,只有
 这三个状态能够以非零的概率被访问,所以
这三个状态能够以非零的概率被访问,所以
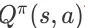 可以简化为
可以简化为
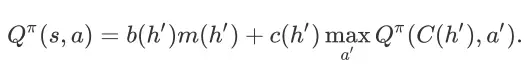
在这里,
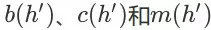 分别为 item page history
分别为 item page history
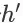 对应的成交转化概率、继续会话概率和成交价格期望。一般地,我们会用一个带参函数
对应的成交转化概率、继续会话概率和成交价格期望。一般地,我们会用一个带参函数
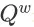 来对
来对
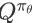 进行近似计算,其优化目标是最小化参数 w 的均方误差(MSE,Mean Squared Error)
进行近似计算,其优化目标是最小化参数 w 的均方误差(MSE,Mean Squared Error)
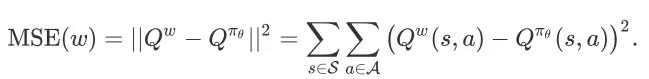
而 MSE(w)关于 w 的梯度为
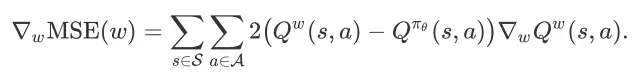
由于
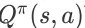 未知,我们无法准确地计算出
未知,我们无法准确地计算出
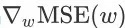 的值。一个普遍的做法是将
的值。一个普遍的做法是将
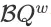 作为
作为
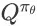 的代替来计算出
的代替来计算出
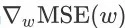 的近似值,所以我们可以得到
的近似值,所以我们可以得到
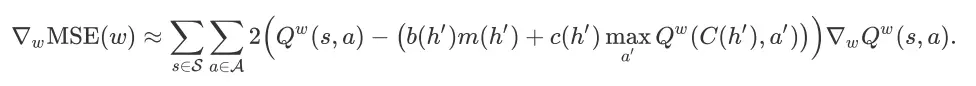
其中,
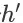 表示(s, a)引导的 item page history。在我们实际采用随机梯度法来优化 w 时,就能用一种完全回退(full backup)的方式来对 w 进行更新。具体地,对于我们观察到的任意状态动作对(s, a)及其对应的 item page history
表示(s, a)引导的 item page history。在我们实际采用随机梯度法来优化 w 时,就能用一种完全回退(full backup)的方式来对 w 进行更新。具体地,对于我们观察到的任意状态动作对(s, a)及其对应的 item page history
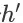 ,w 的变化量为
,w 的变化量为
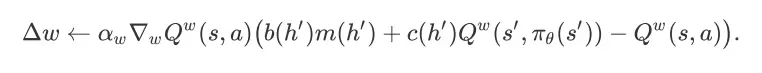
在这里,
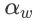 为学习率,
为学习率,
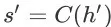 为 item page history
为 item page history
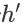 对应的继续会话事件。这种完全回退的更新方法可以避免单步样本回退方法(one-step sample backup)带来的采样误差。同时,在我们的问题中,这种完全回退方法的计算量并不比单步样本回退方法的计算量大。
对应的继续会话事件。这种完全回退的更新方法可以避免单步样本回退方法(one-step sample backup)带来的采样误差。同时,在我们的问题中,这种完全回退方法的计算量并不比单步样本回退方法的计算量大。
我们的策略梯度算法在确定性策略梯度定理 [8] 和对 Q 函数的完全回退估计的基础上提出,我们将其命名为 Deterministic Policy Gradient with Full Backup Estimation (DPG-FBE)。与已有的基于模型的强化学习算法 [10,11] 不同,DPG-FBE 算法并不需要维护完整的奖赏函数和状态转移函数模型,而只需要对 Search Session MDP 中的成交转化概率模型
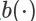 、继续会话概率模型
、继续会话概率模型
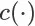 和成交价格期望模型
和成交价格期望模型
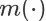 进行建模。任何可能的统计学习方法都可以用来对这三个模型进行在线或离线地训练。DPG-FBE 的细节展示在算法 1 中。
进行建模。任何可能的统计学习方法都可以用来对这三个模型进行在线或离线地训练。DPG-FBE 的细节展示在算法 1 中。

如算法 1 所示,DPG-FBE 算法的策略函数参数 和值函数参数 会在每个搜索会话结束后进行更新。为了保证算法学习到好的排序策略,探索(Exploration)机制必不可少(算法第 行)。对于离散动作空间问题,探索可以通过 -贪心方法实现;而对于连续动作空间问题,探索则可以通过对 的输出添加高斯噪音来实现。DPG-FBE 算法并未对策略函数 和值函数 采用的具体模型做任何假设,但由于 Search Session MDP 通常具有很大的状态空间和动作空间,所以我们建议尽量采用非线性模型(例如:神经网络)来进行学习。为了确保学习的稳定性以及解决函数近似带来的收敛性问题,样本池(replay buffer)和目标更新(target update)等 [12, 13] 在深度强化学习中广泛应用的技巧,也建议在 DPG-FBE 算法的具体实现中采用。
五、实验与分析
为了对 DPG-FBE 算法的性能进行验证,我们进行了两组实验。在第一组实验中,我们构建了一个简易的在线购物模拟器,并对 DPG-FBE 算法以及目前最新的几个 online LTR 算法进行对比测试。在第二组实验中,我们将 DPG-FBE 算法在淘宝搜索引擎中进行投放,以检验其实际应用效果。
5.1 模拟实验
模拟实验中使用的在线购物模拟器基于淘宝中部分商品和用户的统计信息构建。其中,商品被表示为形如
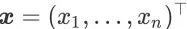 的 n 维特征向量。搜索引擎的排序动作也是一个 n 维向量,我们用
的 n 维特征向量。搜索引擎的排序动作也是一个 n 维向量,我们用
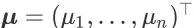 来表示。对于任意商品
来表示。对于任意商品
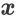
,它在排序动作
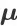 作用下的打分为
作用下的打分为
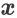 和
和
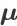 的内积
的内积
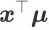 。我们选择了连衣裙类目商品的 20 个重要商品特征,并根据这些特征的分布进行随机采样,生成了 1000 个虚拟的商品。搜索会话中展示给用户的每一个商品页面包含 10 个商品。因此,一个搜索会话最多会包含 100 轮排序。用户在每个商品展示页面的行为(比如:点击、购买、离开等)通过用户行为模型进行模拟,该模型是从淘宝的连衣裙类目的用户行为数据中构建的。在一个搜索会话中,给定最近展示的 个商品展示页面,用户行为模型将输出用户点击商品、购买商品、继续会话以及离开会话的概率。一个搜索会话将在用户购买商品或者离开会话时结束。
。我们选择了连衣裙类目商品的 20 个重要商品特征,并根据这些特征的分布进行随机采样,生成了 1000 个虚拟的商品。搜索会话中展示给用户的每一个商品页面包含 10 个商品。因此,一个搜索会话最多会包含 100 轮排序。用户在每个商品展示页面的行为(比如:点击、购买、离开等)通过用户行为模型进行模拟,该模型是从淘宝的连衣裙类目的用户行为数据中构建的。在一个搜索会话中,给定最近展示的 个商品展示页面,用户行为模型将输出用户点击商品、购买商品、继续会话以及离开会话的概率。一个搜索会话将在用户购买商品或者离开会话时结束。
我们采用深度神经网络作为策略函数和值函数的模型,实现了 DPG-FBE 算法的深度强化学习版本 DDPG-FBE。同时,我们也实现了 DPG 算法的深度强化学习版本,即 DDPG 算法 [13]。环境的状态是从当前搜索会话的最近 4 个商品页面中抽取的 180 维特征向量。DDPG-FBE 和 DDPG 两个算法的网络结构和参数采用相同的设置:(1)actor 和critic 网络都采用 2 个全连接的隐层,第一个隐层包含 200 个单元,第二个隐层包含 100 个单元,隐层所有单元的激活函数都是 \textit{relu};(2)actor 网络的输出层包含 20 个单元,每个单元的激活函数为 \textit{tanh},critic 网络的输出层只有 1 个单元,无激活函数;(3)actor 网络的输出会作为输入接到 critic 网络的第二个隐层前;(4)actor网络和 critic 网络的参数通过 Adam 算法进行优化,学习率分别为
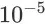 和
和
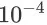 ;(5)目标网络的更新比例
;(5)目标网络的更新比例
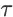 设置为
设置为
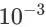 。我们设置了 0、0.1、0.5、0.9 和 1.0 五组折扣率,分别测试 DDPG-FBE 算法和 DDPG 算法在不同折扣率下的性能。同时,为了和两个强化学习算法进行对比,我们也实现了五个 online LTR 算法:point-wise LTR 算法、BatchRank 算法 [1]、CascadeUCB1 算法 [2]、CascadeKL-UCB 算法 [2] 和 RankedExp3 算法 [3]。同 DDPG-FBE 和DDPG 类似,我们实现的 point-wise LTR 算法学习也是在搜索会话的每个状态下输出一个 20 维的排序权重向量。我们采用深度神经网络作为 point-wise LTR 的模型,并用 logistic regression 算法对其进行训练,训练目标为最大化总成交额。其他的 online LTR 算法则是基于的多臂老虎机模型的遗憾最小化算法(regret minimization algorithm)。对每个算法的测试包含 100,000 个搜索会话,我们记录下被测算法在每个搜索会话中引导的成交额,并将结果展示在图 3、图 4 和图 5 中。
。我们设置了 0、0.1、0.5、0.9 和 1.0 五组折扣率,分别测试 DDPG-FBE 算法和 DDPG 算法在不同折扣率下的性能。同时,为了和两个强化学习算法进行对比,我们也实现了五个 online LTR 算法:point-wise LTR 算法、BatchRank 算法 [1]、CascadeUCB1 算法 [2]、CascadeKL-UCB 算法 [2] 和 RankedExp3 算法 [3]。同 DDPG-FBE 和DDPG 类似,我们实现的 point-wise LTR 算法学习也是在搜索会话的每个状态下输出一个 20 维的排序权重向量。我们采用深度神经网络作为 point-wise LTR 的模型,并用 logistic regression 算法对其进行训练,训练目标为最大化总成交额。其他的 online LTR 算法则是基于的多臂老虎机模型的遗憾最小化算法(regret minimization algorithm)。对每个算法的测试包含 100,000 个搜索会话,我们记录下被测算法在每个搜索会话中引导的成交额,并将结果展示在图 3、图 4 和图 5 中。
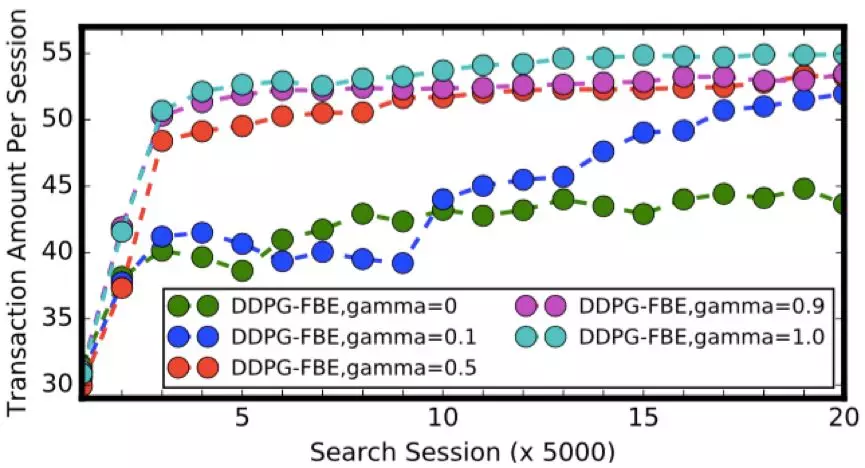
图 3. DDPG-FBE 算法在模拟实验中的测试结果
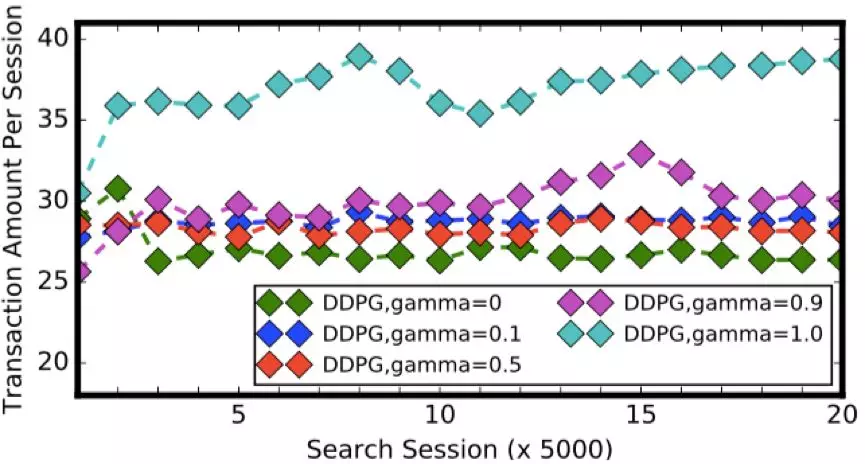
图 4. DDPG 算法在模拟实验中的测试结果
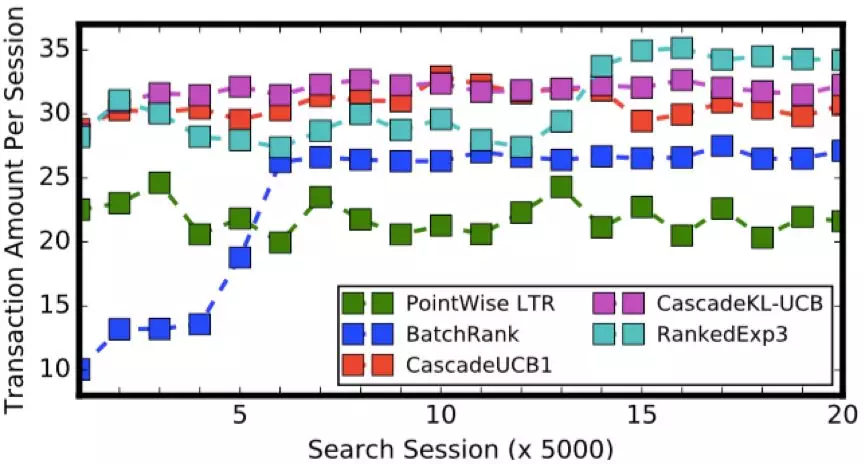
图 5. 五个 online LTR 算法在模拟实验中的测试结果
首先考察 DDPG-FBE 算法的测试结果。从图 3 中可以看到,随着折扣率 y 变大,DDPG-FBE 算法的性能逐渐改善。DDPG-FBE 算法在折扣率 y = 0 时引导的成交额要远远低于它在其他折扣率下引导的成交额。由于 y = 0 表示只考虑最大化即时奖赏,这样的结果也就说明延迟奖赏在搜索排序决策中的重要性。不难发现,DDPG-FBE 算法在折扣率 y = 1 时引导的成交额最大(比第二好的结果高出 2%),这也进一步验证了我们在上一节给出的理论结果。值得一提的是,在淘宝搜索这样的大规模场景中,即便是 1% 的提升也是很可观的。同样地,DDPG 算法也是在折扣率 y = 1 时引导了最高的成交额。然而,与 DDPG-FBE 算法相比,DDPG 算法并没有学到很好的排序策略。如图 4 所示,DDPG 算法所有的学习曲线最终在 y 轴方向都没有超过 40,而 DDPG-FBE 算法在 y = 1 时最终收敛到 55 左右。我们测试的 5 个 online LTR 算法引导的成交额都没能超过 DDPG 算法引导的最高成交额。由于这些算法并非为多步排序决策问题所设计,所以这样的结果并不奇怪。
5.2 搜索排序应用
第二个实验是一个实际的应用。我们将 DDPG-FBE 算法应用到淘宝搜索引擎中,提供实时在线商品排序服务。淘宝的搜索任务面临两大挑战,一个是大量在线用户导致的高并发度的需求,另一个则是对用户所产生的海量数据的实时处理。具体来说,淘宝搜索引擎每秒需要同时响应数十万计的用户的搜索请求,并同时处理这些用户产生的行为数据。在大促活动中(比如:天猫双十一),在淘宝中产生的数据量以及数据产生速度都要比平时高数倍。
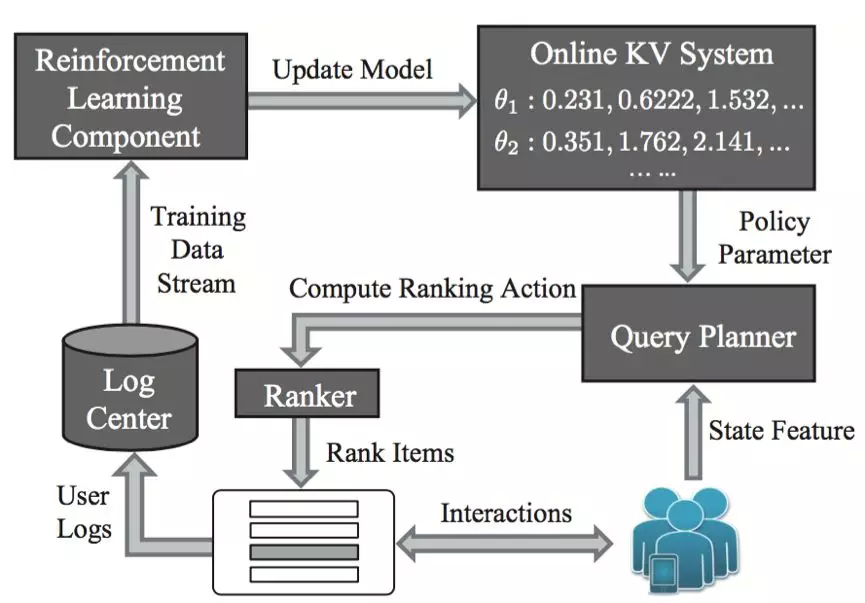
图 6. 基于数据流的强化学习排序系统构架
为了满足对高并发度和海量数据处理的需要,我们设计了一套基于数据流的强化学习商品排序系统,并在此基础之上实现 DPG-FBE 算法。如图 6 所示,整个系统主要包含五个部分:查询规划器(关键词 planner)、排序打分器(ranker)、日志中心(log center)、强化学习组件和在线 KV 系统(online KV system)。从图中可以看到,系统的工作过程由两个循环构成:其中一个循环代表用户和搜索引擎之间的交互过程(图中右下角的循环),也是搜索引擎执行排序动作的地方,我们称其为 online acting loop;另一个循代表学习算法的训练过程(图中靠左的大循环),我们称其为 learning loop。这两个循环通过日志中心和在线 KV 系统相连接。
在 online acting loop 中,每当有用户发出商品页面的请求时,查询规划器(关键词 planner)将抽取当前搜索会话的状态特征,从在线 KV 系统中获取当前的排序策略模型参数,从而计算出当前状态下搜索引擎的排序动作。在这之后,排序打分器(ranker)将接收这个排序动作,对商品进行打分,并将 Top K 商品展示到一个商品页面中。用户看到该商品页面之后,就能对页面上的商品进行相应的操作。与此同时,用户在商品页面上的各种行为将会以日志的形式记录到日志中心,作为训练学习算法的数据源。在日志中心,从不同搜索会话中产生的用户日志数据都会转化为形如 ( s,a,r,s’)的训练样本。这些样本将以数据流的形式不断地输出给强化学习组件,用于策略模型参数的更新。每当策略模型有更新时,新的模型将被写入在线 KV 系统。这时,搜索引擎就可以采用更新后的排序策略来产生排序动作,对商品进行排序。需注意的是,整个系统的两个循环是并行的,但并非同步。这是因为,用户在搜索会话中产生的行为日志并不能立即被用来对算法进行训练。
我们仍然采用模拟实验中线性点乘模式对商品进行排序。搜索引擎的排序动作是 27 维的权重向量。在一个搜索会话中,环境的状态是一个 90 维的特征向量,包含了当前搜索会话中的用户特征、关键词特征和商品页面特征。与模拟实验不同,淘宝中的搜索排序服务面向所有类型的用户,且对输入关键词没有任何限制,所以我们也将用户和关键词的信息加入到状态中。我们仍然采用神经网络作为策略函数和值函数的模型,两个网络都包含两个全连接隐层。其中,第一个隐层包含 80 个单元,第二个隐层包含 60 个单元。由于淘宝搜索排序服务对实时性能和数据快速处理有很高的要求,所以实验中策略函数和值函数模型的网络规模要比模拟实验中采用的网络规模小很多。我们在基于数据流的强化学习商品排序系统中分别实现了 DDPG 和 DDPG-FBE 算法,并进行了为期一周的 A/B 测试。在每天的测试中,DDPG-FBE 算法引导的成交额都要比 DDPG 算法引导的成交额高 2.7%~4.3%。在 2016 年的双十一当天, 我们也将 DDPG-FBE 算法进行了线上投放。同基准的算法相比 (一个离线训练的 LTR 算 法),DDPG-FBE 算法带来了 30% 的成交额提升。 _
 _
_
参考文献
[1] Masrour Zoghi, Tomas Tunys, Mohammad Ghavamzadeh, Branislav Kveton, Csaba Szepesvari, and Zheng Wen. 2017. Online Learning to Rank in Stochastic Click Models. Proceedings of the 34th International Conference on Machine Learning (ICML’17), 4199–4208.
[2] Branislav Kveton, Csaba Szepesvari, Zheng Wen, and Azin Ashkan. 2015. Cas- cading bandits: Learning to rank in the cascade model. In Proceedings of the 32nd International Conference on Machine Learning (ICML'15), 767–776.
[3] Filip Radlinski, Robert Kleinberg, and Thorsten Joachims. Learning di- verse rankings with multi-armed bandits. In Proceedings of the 25th international conference on Machine learning (ICML'08), 784–791.
[4] Sumeet Katariya, Branislav Kveton, Csaba Szepesvari, Claire Vernade, and Zheng Wen. 2017. Stochastic Rank-1 Bandits. In Artificial Intelligence and Sta- tistics. 392–401.
[5] Paul Lagree, Claire Vernade, and Olivier Cappe. 2016. Multiple-play bandits in the position-based model. In Advances in Neural Information Processing Systems (NIPS’16). 1597–1605.
[6] Ronald J Williams. 1992. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Machine learning 8, 3-4 (1992), 229–256.
[7] Richard S Sutton, David A McAllester, Satinder P Singh, and Yishay Mansour. 2000. Policy gradient methods for reinforcement learning with function approxi- mation. In Advances in Neural Information Processing Systems (NIPS’00). 1057– 1063.
[8] DavidSilver,GuyLever,NicolasHeess,ThomasDegris,DaanWierstra,andMar- tin Riedmiller. 2014. Deterministic policy gradient algorithms. In Proceedings of the 31st International Conference on Machine Learning (ICML’14). 387–395.
[9] R.S. Sutton and A.G. Barto. 1998. Reinforcement Learning: An Introduction. MIT Press.
[10] Michael Kearns and Satinder Singh. 2002. Near-optimal reinforcement learning in polynomial time. Machine Learning 49, 2-3 (2002), 209–232.
[11] Ronen I. Brafman and Moshe Tennenholtz. 2002. R-MAX - A General Poly- nomial Time Algorithm for Near-Optimal Reinforcement Learning. Journal of Machine Learning Research 3 (2002), 213–231.
[12] VolodymyrMnih,KorayKavukcuoglu,DavidSilver,AndreiARusu,JoelVeness, Marc G Bellemare, Alex Graves, Martin Riedmiller, Andreas K Fidjeland, Georg Ostrovski, et al. 2015. Human-level control through deep reinforcement learning. Nature 518, 7540 (2015), 529–533.
[13] Timothy P Lillicrap, Jonathan J Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuv
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/%E4%BA%92%E8%81%94%E7%BD%91/%E7%94%B5%E5%95%86%E6%90%9C%E7%B4%A2%E5%9C%BA%E6%99%AF%E4%B8%AD%E7%9A%84%E5%BC%BA%E5%8C%96%E6%8E%92%E5%BA%8F%E5%AD%A6%E4%B9%A0%E5%BD%A2%E5%BC%8F%E5%8C%96%E7%90%86%E8%AE%BA%E5%88%86%E6%9E%90%E4%BB%A5%E5%8F%8A%E5%BA%94%E7%94%A8/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


