作者：朱小强（怀人）

0. 序曲

纵观这两年业界技术的演化趋势，几乎主流的团队都已经完成了深度学习为代表的技术升级，进入到算力吃紧、模型红利放缓的新瓶颈期。去年在 《深度学习推荐系统》序言 一文中，我对工业级深度学习技术迈入新的 2.0 进阶阶段的特征做过一些探讨：

可以预见，在工业级深度学习2.0阶段，技术演进的模式将再升级：从算法视角的实践和问题驱动，进一步拓展到更宏大的技术体系整体思考：领域问题特性、数据、算力、算法、架构及工程系统等将被纳入统一的思考框架中，成为技术创新的发力点

从 2018 年开始我们团队就开始做相应的布局。除了在算法层面持续开辟纵深战场外，对于"算力"这件事我们做了大量细致的工作，这几年支撑了我们的核心广告模型一路从 DIN(2017)、 DIEN(2018)、 MIMN(2019)，升级到今年的 SIM(2020)、 CAN(2020)。值得一提的是，在业界普遍陷入滞涨的这个阶段，今年我们一年内完成了 SIM 和 CAN 两个大版本主模型的研发和全量上线，同时叠加在主模型之上的多场景、多目标建模也都有所突破，核心场景取得了 CTR/RPM 累积提升超过 20%的巨大收益，这是继 2017 年 all in 深度学习之后我们达到的第二个技术创新小高峰。

印象中直到今天，还有不少同学对我们宣称 DIEN 这样的复杂模型能够在广告系统全流量服务报以怀疑的态度。的确，在这种大规模的广告系统中支持 GRU-based 模型的在线实时 inference，即使是 18 年模型生产化之初我们的工程同学也是有担忧的。然而实际情况是，相比于今年的 SIM 及 CAN 模型而言，DIEN 的 inference 算力需求不过是开胃小菜了。另一方面，不仅仅是 ranking 模型，我们的广告召回模型、粗排模型，甚至后链路的机制策略、rerank 模型等，都面临着相似的恐怖算力激增挑战。如何解决这个问题呢？18 年的时候我做过一个断言：

占领算力效能的制高点，将成为头部团队在工业级深度学习2.0阶段算法继续创新突破的胜负手

幸运的是，经过近 3 年的辛苦跋涉，我们终于在转角处闻到了蔷薇的花香。近期我们陆续开始把一些成型的工作总结和分享出来，希望能够给大家带来一些启发，如：model design 和 model inference 相结合的 MIMN； 算法与系统 co-design 思路下重新设计的粗排系统 COLD；以及被今年 DLP-KDD 2020 收录且评选为 best paper runner-up 的 “个性化算力"分配算法DCAF。

如果说以上工作更多 focus 在局部模块进行了 algorithm 和 system 的 co-design，那本文则是我们这一思想的更深度推进：进一步发展"个性化算力"技术，将算力融合到广告引擎的设计中，形成更全面立体的算力解决方案，同时也给古典的引擎系统赋予了全新的动力。“算力经济时代” 看起来有点标题党，但我认为这是对算力在这个时期技术版图中重要性的最好注解了。

以下是本文的具体内容，来自阿里展示广告技术团队(致谢相关兄弟团队的大力支持)。友情提醒，它解决的不是传统的算法或者引擎领域问题，因此不一定适合所有读者。哪怕是广告、推荐领域的从业者，如果没有接触或者思考过这类命题，亦或是对引擎系统的细节了解不多，读起来也会有点艰涩。

1. 导读

时间的焦距拉到 5 年前，谁也不会预料到以深度学习为代表的 AI 变革，对业界技术的重塑力度会如此之大、影响如此之深。这背后的一个重要变量就是"算力”。随着深度学习技术上的大量创新，广告、推荐等在线引擎系统的架构和算法复杂度迅速飙升，对算力的需求出现了爆发式的增长。以阿里展示广告系统为例，相比于 5 年前的精排模型，其在线算力的需求暴涨了近 2 个数量级[2,3,4]。如此惊人的算力需求增速，仅仅靠 GPU/NPU 等硬件的演化已然不足，更不用说硬件本身已经在逼近摩尔定律极限。

面临着算力供给触及瓶颈的巨大危机，我们看到不论是工业界还是学术界都在积极寻找解法。阿里展示广告团队从 18 年起就开始布局算力效能技术的研发，目前已经迈入了第 3 代算力效能体系的阶段：

  1. 算力效能1.0阶段 (2018)：聚焦单点工程优化及模型瘦身优化等技术
  2. 算力效能2.0阶段 (2019)：将Model Design和Engineering Optimization结合，通过算法-工程Co-design方法论的深度实践，带来了显著红利
  3. 算力效能3.0阶段 (2020)：从引擎单模块进一步拓展到系统全链路，用"个性化"算力的思想去重新审视和改造了整个广告引擎系统，为古典在线引擎注入了新的活力，让它变得更加"柔性"：充分提升给定算力的性价比，让其在面临任意复杂、动态的业务需求和流量环境时能够自适应地做到 算力最优使用。

结合了算力效能视角的展示广告引擎，我们命名为 Transformers（致敬变形金刚），本文将分享我们的实践经验和思考。值得一提的是，算力效能感知的柔性广告引擎（Computing Power-aware Transformers Engine）今年已经真正落地于阿里展示广告业务：

1. 业务效果上： 仅广告精排的个性化算力优化就能够带来RPM持平下算力节省25%、同等算力下RPM提升2%的收益[1]；

2. 系统能力上： 具备柔性能力的广告在线系统平稳地应对了双十一的各种流量波动和日常的各类系统异常，大幅提升了系统稳定性和运维效率。

2. 开胃菜：先来看看算力分配这件事

我们可以从微观和宏观的层面来理解在线系统的算力分配问题。

  1. 微观上：在某一时刻，不同流量的价值不同，算力消耗也不同——也就是算力性价比不同。我们可以根据算力性价比，为每个流量分配更合理的算力(计算资源/Latency约束等)，从而在系统总算力的约束下，实现业务收益的全局最优。
  2. 宏观上：由于流量大小和分布会随时间不断变化，那么在总算力约束下，算力分配策略也需要动态调整，来保持业务收益的动态最优。这种微观和宏观相结合的视角，能够有效地帮助我们拆解问题。

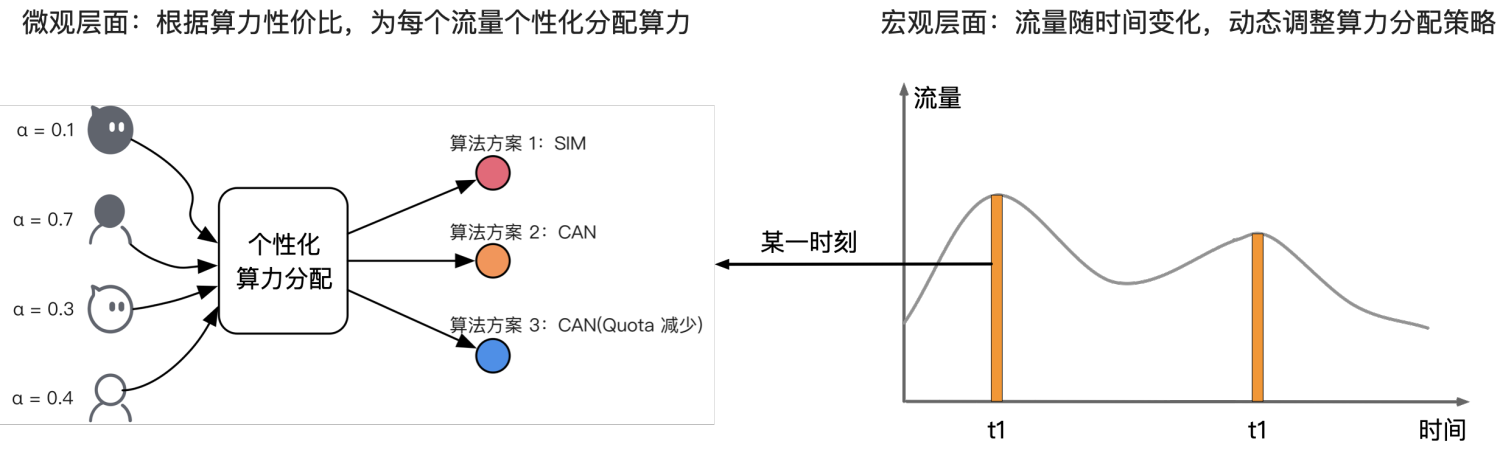
图 1：算力分配的微观 &宏观视角

Transformers 引擎的核心理念，就是将算力分配纳入到系统的设计范畴。对于古典广告引擎而言，其使命是确保引擎系统能够准确地实现和运行业务逻辑。对任意一条流量请求，原则上执行的计算逻辑是一致的(这里仅考虑算力差异化视角)。在资源充足时这是合理的策略，但在算力紧张、需要腾挪资源甚至算法策略降级才能在特定的系统资源约束下完成业务逻辑时，这背后就隐藏着巨大的效能空间。以广告系统为例，我们可以选择：1. 开足算力对每条流量做最精细化最复杂的计算，对超出系统算力的部分流量做丢弃操作； 2. 对不同价值的流量做差异化的算力规划，确保系统对每条流量都有效服务。 哪种策略是最优？这就是 Transformers 引擎的目标：在有限的资源中做"柔性"算力伸缩，确保业务收益最大化。

3. 形式化：算力分配的数学化表达

我们来具体分析宏观、微观两个层面的算力分配问题。首先，我们需要具象化地理解“算力”。系统算力往往被计算相关的参数控制，包括算法策略参数(检索 token 数/打分 doc 数/模型版本等)和系统性能参数(线程数/缓存规则等)。在线系统通常会包含很多这样的算力参数。我们用“档位”来描述这些算力参数的取值，不同档位代表不同的算力消耗。档位选择的过程就是算力分配的过程。对某个算力参数来说：流量i需要在K个候选档位中选择一个档位，其中第 j个候选档位 action_{i,j}​ 将会带来 cost_{i,j}​的算力消耗和 value_{i,j}​的业务收益。

微观层面： 对某一时刻 t，若用 s(i)表示流量 i 选择的算力档位，那么该时刻的算力分配问题可以描述为：该时刻的 N(t)个流量的总算力消耗 \sum_{i \leq N} cost_{i,s(i)}在不超过总算力约束 C 的前提下，如何最大化总业务收益 \sum_{i \leq N(t)} value_{i,s(i)} 的问题。

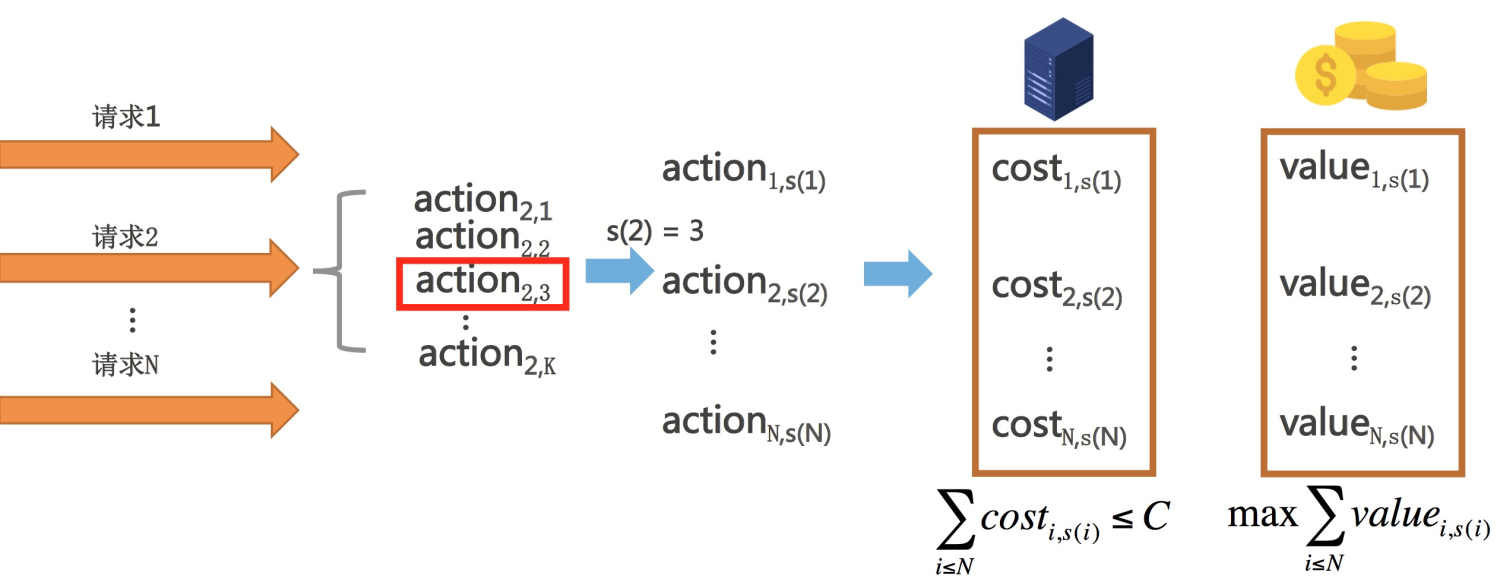
图 2：算力分配问题定义

宏观层面： 对不同时刻 t，流量大小 N(t)在不断变化，但系统的总算力约束 C通常会相对稳定。我们将某一时刻在 \sum_{i \leq N} cost_{i,s(i)} \leq C 约束下的 \max_s \sum_{i \leq N} value_{i,s(i)} ​策略推广到所有时刻，理论上就可以实现动态的算力最优分配。

在下文中，我们将分别介绍特定时刻下的算力分配算法和考虑宏观变化下的系统实现。

4. 静态算力最优分配：DCAF 算法

首先我们来看某一时刻的算力最优分配求解。延续上文的形式化定义，将算力配置选择 s(i)用 one-hot 向量的方式表示为待优化变量 x(i)，即： x_{i,j} = 1 ~~if~s(i) = j, ~otherwise ~~x_{i,j}=0，则优化目标和约束定义如下：

\max_{x \in dom X} \sum_{i \leq N, j \leq K} x_{i,j} \ value_{i,j} \\ s.t.(\sum_{i \leq N, j \leq K} x_{i,j} \ cost_{i,j}) \leq C

  • Lagrangian求解思路

这里为大家介绍我们团队自研的 DCAF个性化算力分配算法。我们使用 Lagrangian 方法来求解这个带约束的优化问题，引入额外变量 λ：

L(x, \lambda) = -\sum_{i \leq N, j \leq K} x_{i,j} \ value_{i,j} + \lambda(\sum_{i \leq N, j \leq K} x_{i,j} \ cost_{i,j} - C)

并相应地构造对偶函数g(λ)：

g(\lambda) = \min_{x \in dom X} -\sum_{i,j} x_{i,j} \ (value_{i,j} - \lambda cost_{i,j}) - \lambda C \\ = -[\sum_{i \leq N}\max_{j \leq K}(value_{i,j} - \lambda cost_{i,j}) + \lambda C]

可以看出，对于任意给定的 λ，对偶函数g(λ)在s(i) = \arg\max_{j \leq K} (value_{i,j} - \lambda cost_{i,j})时最优。注意：每个流量 i的最优档位 s(i)可以独立求解，因此非常适合在实际的分布式系统中进行线上服务。

  • λ的含义：算力边际收益的约束

对于流量 i，在给定λ下，若档位 j优于档位 j′，则：value_{i,j} - \lambda cost_{i,j} > value_{i,j’} - \lambda cost_{i,j’}​，即： \frac{ \Delta value_{j’ \rightarrow j} }{ \Delta cost_{j’\rightarrow j} } λ。也就是说：一个档位相比另一档位更优，当且仅当其算力边际收益

\frac{\Delta value }{\Delta cost }> \lambda 。因此， 可以认为 λ 是对算力边际收益的约束。

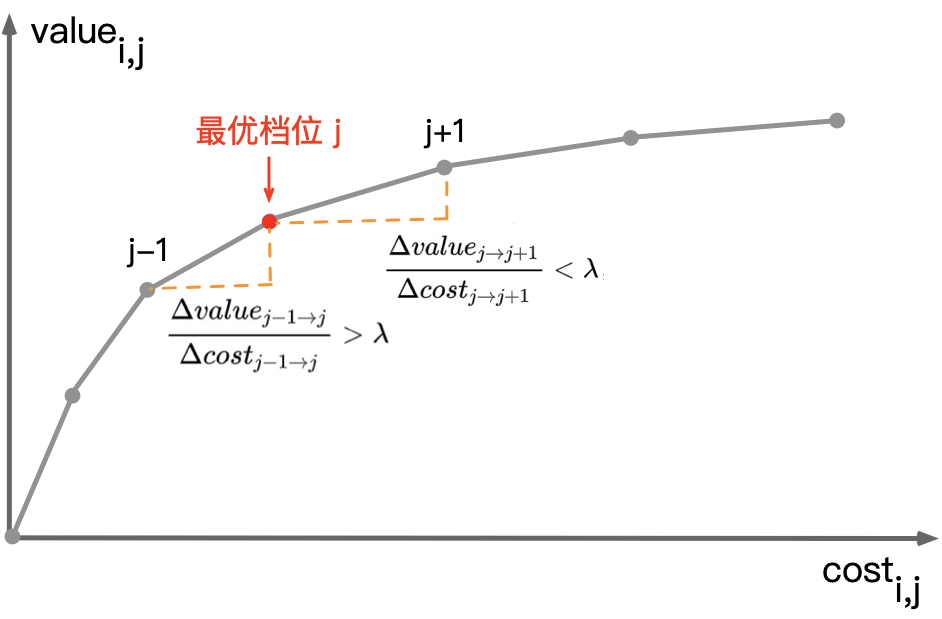
图 3：算力消耗-收益曲线(边际收益递减)

不难看出，λ越小(放宽性价比约束)最优档位j就越大，对应的算力消耗和业务收益也越大，反之亦然。因此， 总消耗和总收益会随着λ减小而单调递增，而整体算力性价比会随着λ减小而单调递减。

  • λ的求解：算力约束的临界状态

知道了λ的含义，接下来看使得g(λ)最优的λ如何计算。由单调性和算力约束可以想到，尽可能地多用算力可最大化价值。而稍加整理也能看到g(λ)的现实含义就是“已使用算力的总收益” + “λ倍的剩余可用算力"。通过分析λ减小/增大时这两部分的增减量，可以发现当\\算力恰好被用完时 \\ \sum_{i \leq N} cost_{i,s(i)} = C，此时g(λ∗)取到极大值。由弱对偶性可知，此时的g(λ∗)对应的解也正是全局最优解。

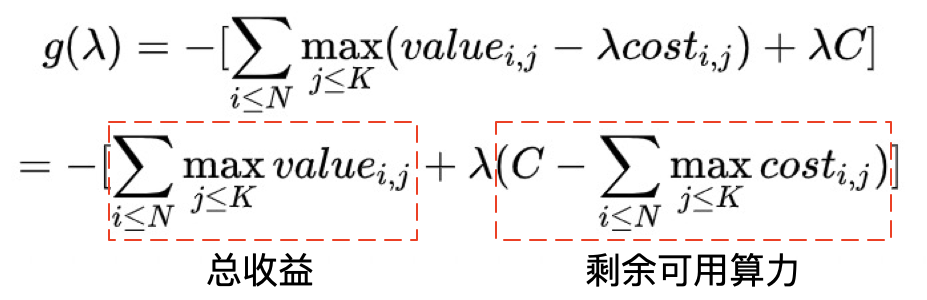
因此，在离线静态求解λ时， 利用算力总消耗随λ减小而单调增加的性质，我们只需通过二分查找去找到最接近算力约束C的λ即可。而面对在线流量的连续变化，我们也无须每时每刻重新求解λ，只需根据每一时刻的算力消耗和算力约束的相对关系，对λ进行实时微调即可——全局维护当前时刻的λ(t)并统计当前时刻的总算力消耗 \sum_{i \le N_t} cost_{i, s(i)}。若当前时刻总算力消耗超过了C，则在下一时刻通过上调λ_{t+1}​来降低算力消耗从而满足约束，反之亦然。由此，在流量平稳时，通过动态维持总算力消耗恰好满足算力约束，几乎可以保证每时每刻系统都处在最优的算力分配状态；而当流量突变时，系统也可以在较短时间内调整到满足约束的状态。具体的系统方案将在下面章节展开。

  • 流量价值/消耗预估和最优档位求解

当在线流量i到来时，只需要得到各档位预估的流量价值value_{i,j}​、算力消耗cost_{i,j}​以及当前的λ，就可以计算出最优档位。那么，流量价值value_{i,j}​和算力消耗 cost_{i,j}如何预估呢？

对于流量价值预估，可以通过分场景或者分用户统计历史 RPM 均值。对于算力消耗预估，取决于算力参数的选取，通常只要找到可量化的算力指标并且在档位间相对可比即可（例如，召回阶段选取检索标签数、海选广告数作为参数，预估阶段选取特征数、广告数作为参数）。以精排阶段的算力分配为例，个性化算力分配可以在广告 RPM 收益不折损的情况下，节省 25%的精排打分算力。而相比不做个性化算力分配，在同等算力下可以提升广告 RPM 约 2%。个性化算力分配为业务增长打开了显著空间，并且该算法方案不局限于单个模块、单个算力参数，可以推广到整个系统。关于 DCAF 算法的更多细节，可以参见我们的论文[1]。

5. 动态算力最优分配：AllSpark 架构

  • 实时反馈调节

以上介绍的 DCAF 算力分配算法，可以在微观层面解决某一时刻的算力最优分配问题。该方法如果推广到所有时刻，在宏观层面实现动态的算力最优分配，关键点在于让“作为算力性价比约束的λ”动态保持最优——λ过大则有可能算力用不完出现浪费，反之λ过小则有可能超出算力约束。上文已经提到了“根据每一时刻的算力消耗和算力约束的相对关系，对λ进行实​时微调”的思路，那么就需要让在线系统具备实时反馈调节的能力，一方面争取让算力“恰好用完”(既满足算力约束又不浪费)，另一方面确保系统稳定可用(对于高可用低延时的广告引擎系统来说，“算力约束”不仅指的是计算资源的约束，还包括了 Latency 的约束)。因此我们选择了**“模块调用失败率”**（由资源不足和其他异常导致的调用超时和错误）作为主要调控指标，根据实时反馈的模块失败率来调节全局的 λ，从而实现动态的算力最优分配。当然，这里的调控标的指标在不同的引擎系统中可以选择不同的锚点，一个可供参考的原则是：选择对算力的波动最敏感的系统指标。

  • 系统设计实现

DCAF 算力分配算法中的 λ、最优档位 i是针对每个算力参数的，也就是这个参数在所有流量上共享一个全局的 λ，也可以认为所有流量的平均档位对应一个全局的 λ 。为了便于理解和简化实现， 在线系统可以考虑直接对每个参数的平均档位进行实时调节。另一方面，为了实现系统整体的算力最优分配，系统的每个模块都定义了不止一个算力参数，这些参数如果分别独立地自我调节，一是非常复杂，二是不容易形成全局最优。因此真实场景中的算力参数设计需要考虑更加全面。例如我们采用了模块失败率作为主要调控目标，那么就可以把同一模块内所有按失败率调节的算力参数聚合成一个 调控单元，一个调控单元由一组 { 调控目标、调控策略、平均档位 } 组成，单元内的所有参数共享调控策略和平均参考档位。

再回到系统设计。实时反馈调节系统可以认为是在线引擎的非侵入式控制器，它既是一套独立的框架，也能够与在线引擎系统密切配合，共同实现算力调节的能力。我们将整体框架取名为 AllSpark(来自于《变形金刚》中的“火种源”，能够赋予机械生命，使它们具有变形的能力)。AllSpark 框架主要由四个部分组成： 调节链路、反馈链路、控制面板、监控视图。

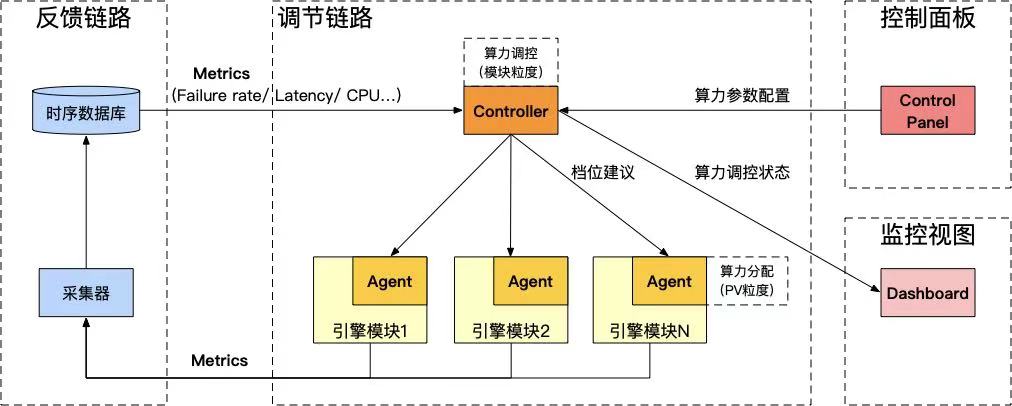
图 4：AllSpark 动态算力框架

调节链路：调节链路包括中控Controller和嵌入在应用模块中的Agent。Controller收集所有模块一段时间内各种调控目标（失败率/Latency/QPS/CPU水位等）的实时指标，并根据一定的调控策略给出每个调控单元的平均档位建议，起到动态调节 λ的作用，同时让各模块满足算力和可用性的约束。Controller作为算力调节的中控，需要做到 稳、准、快。为了满足这些要求，Controller支持了PID控制算法、单步控制、个性化规则等多种调控策略，以及去噪、防抖等平滑机制。Agent是嵌入在每个应用模块中的SDK，它通过从Controller主动拉取该模块所有调控单元的平均档位等调控信息，来确保该模块在平均档位的建议下安全运行。同时，Agent还为每个模块提供了个性化调控的API，可以让各模块自己实现流量粒度的各种个性化算力分配策略（例如DCAF算力分配算法和基于用户质量分的分配算法等）。甚至还可以在Agent中实现下游模块的流控能力。可以看出，Controller-Agent的两级调控机制，既保证了每个模块整体满足算力约束，又能够针对不同流量做个性化的算力分配。

反馈链路： 各模块用于算力调控的指标会通过反馈链路采集到Controller。反馈链路包括采集和存储两部分，我们使用Prometheus收集应用容器中的状态数据，写入时序数据库存储，并为Controller提供查询接口。整个链路目前具备5s左右的反馈时效。

控制面板： 控制面板是人工介入AllSpark的接口，用于分模块/调控单元/场景 多层次地配置和管理 { 调控目标、调控策略、算力档位 }，可以根据情况决定每个参数使用固定档位还是动态档位，并且通过版本控制以及分集群的发布管控，实现可灰度、可回滚的能力。

监控视图： 可以想象，整个系统中数以百计的算力参数实时动态地变化，如果没有完善的监控和异常发现能力，系统随时可能陷入失控的状态。监控视图用于透出每个算力参数的实时/历史平均档位，并且将档位的异常变化对接到监控系统中，让整个AllSpark系统具备可观测的能力。

  • 系统柔性表现

我们以今年双十一大促当天展示广告系统的表现来说明 AllSpark 系统的柔性能力。展示广告场景在双十一零点高峰时段有十倍于日常流量的洪峰。零点之后，流量呈阶梯状逐步回落。往年为了扛住流量洪峰，需要手动推动策略降级预案，并且需要根据流量的变化推送不同版本的降级预案，实现流量和算法策略的最优组合，来确保业务收益最大化。问题在于人工操作的成本很高，风险也很大。AllSpark 的上线使得今年双十一的保障有了很大改观。零点时段只需要推送一个基础版本的降级预案保护，然后通过 AllSpark 根据流量的变化自适应地调节算力，就可以实现系统在高水位下的平稳运行，同时确保了零点黄金时段的业务效果。事实上，仅零点附近 1、2 个小时的系统服务能力增强(用更强的算法策略服务更多的流量)，就给我们今年的广告收入创造了千万人民币规模的收入增量。

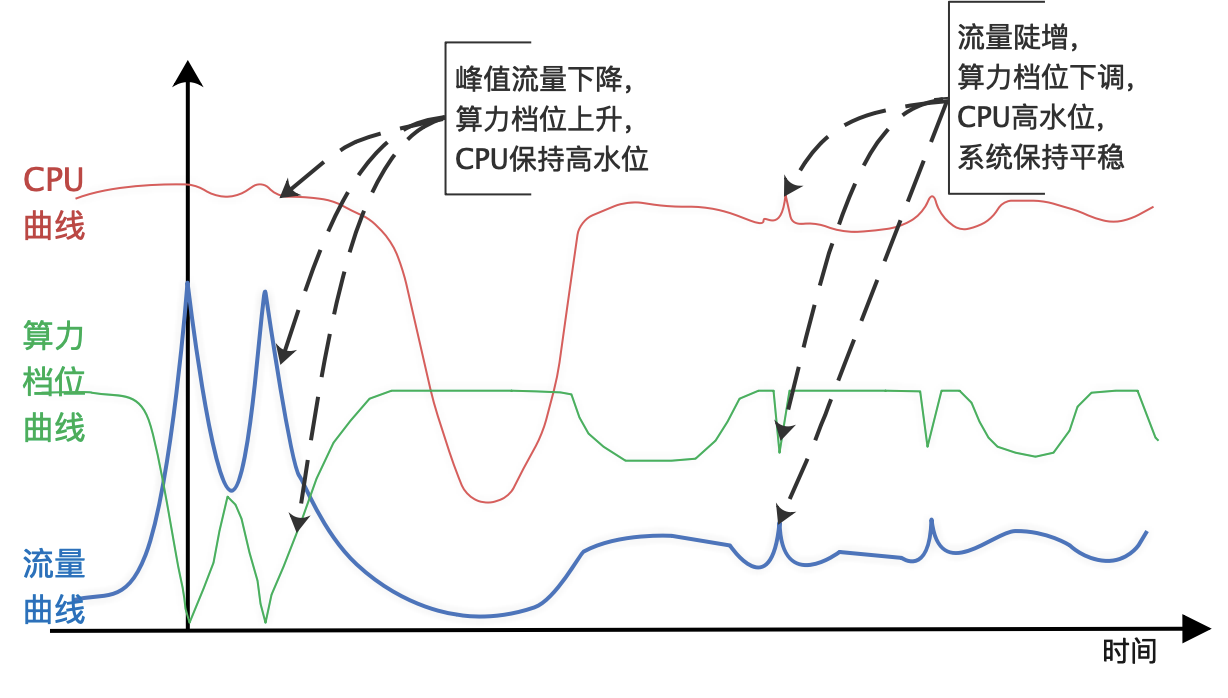
图 5：2020 双十一大促系统表现示意图

除了能够在大促期间柔性应对各种流量洪峰之外，AllSpark 在系统的日常稳定性保障上也发挥了重要作用。当系统偶尔出现局部模块的超时抖动时，AllSpark 能够自动降低问题模块的算力负载、加速问题恢复，从而将故障隔离在局部，确保系统整体的健壮可用。

6. Beyond 算力：再看 Transformers 柔性引擎

个性化算力分配算法+自适应动态算力系统相结合，使得广告引擎系统具备了柔性能力。这样的系统就像变形金刚一样，能够自动变形成最适应环境变化的状态，因此我们也把被赋予了柔性能力的在线系统称作 **Transformers。**事实上，跳出算力视角看 Transformers 柔性系统，它同样赋予了更多的想象力和可能性：

  • 多场景调控：Transformers不仅能在 时间维度 的静态和动态层面实现算力最优分配，还能够在 空间维度 的多场景复杂业务系统中起到算力调控的角色。由于不同业务场景的流量规模和流量价值差异很大，从安全隔离的角度通常做法是分场景独立地部署系统。那么如何为每个场景分配合理的算力并且动态维护最优呢？这往往很难，而且对一些场景快速变化的响应速度是不足的。Transformers给我们提供了一条新的解决方案：无须多场景独立部署，由一套统一的系统(**OneEngine)**高效承接各种异构的流量，从而可以自然地将DCAF和AllSpark的能力从单场景推广到多场景，多场景资源共享的同时实现跨场景的全局算力最优分配、业务收益最大化，以及系统整体平稳可用。
  • 业务系统大脑：Transformers柔性系统区别于传统的负载均衡、自动化限流降级等系统层面的解决方案，它站在业务系统的全局视角，追求算法策略的算力最优分配、业务收益最大化，同时让系统在计算资源利用率、Latency等系统指标上达到最优平衡。可以看出，Transformers实际上扮演了业务系统运行时大脑的角色，这也是我们对在线系统未来演进方向的判断和探索。

Reference

[1]. Jiang et al, *DCAF: A Dynamic Computation Allocation Framework for Online Serving System, * https://arxiv.org/abs/2006.09684

[2]. Pi et al*, Search-based User Interest Modeling with Lifelong Sequential Behavior Data, * https://arxiv.org/abs/2006.05639

[3]. Wang et al*, COLD: Towards the Next Generation of Pre-Ranking System, * [https://arxiv.org/abs/2007.16122](https://www.6aiq.com/f