腾讯技术用万字长文聊一聊技术
作者: qfan,腾讯 WXG 应用研究员
随着深度学习在工业届不断火热,Embedding 技术便作为“基本操作”广泛应用于推荐、广告、搜索等互联网核心领域中。Embedding 作为深度学习的热门研究方向,经历了从序列样本、图样本、再到异构的多特征样本的发展过程。本文主要系统总结了现在主流的 Embedding 技术,简单介绍它们的基本原理,希望对大家快速整理相关知识有所帮助。
一、引言
在提到 Embedding 时,首先想到的是“向量化”,主要作用是将高维稀疏向量转化为稠密向量,从而方便下游模型处理。那什么是 embedding 呢?下面是大家对 embedding 的定义:
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup. – Wikipedia
An embedding is a mapping from discrete objects, such as words, to vectors of real numbers. – Tensorflow 社区
Embedding 是用一个低维稠密向量来表示一个对象,使得这个向量能够表达相应对象的某些特征,同时向量之间的距离能反应对象之间的相似性。 – 王喆《深度学习推荐系统》
将一个实例(instance)从复杂的空间嵌入(投射)到相对简单的空间,以便对原始实例进行理解,或者在相对简单的空间中进行后续操作。 – chrisyi《Network embedding 概述》
我个人比较倾向于 Tensorflow 社区给出的定义,即 Embedding是离散实例连续化的映射。如下图所示,可以将离散型词 embedding 成一个四维的连续稠密向量;也可以将图中的离散节点 embedding 成指定维度的连续稠密向量。
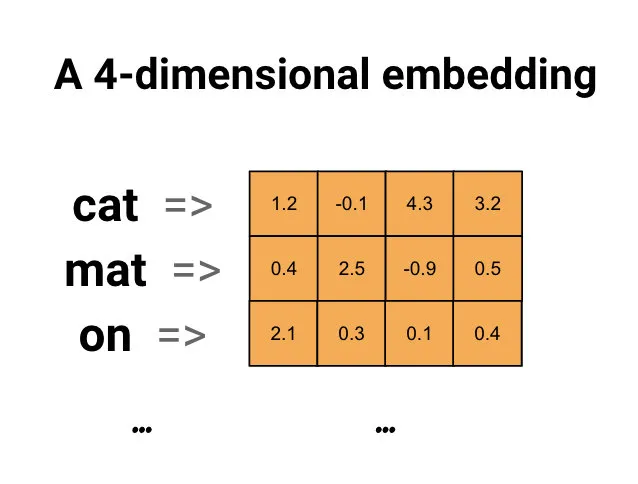
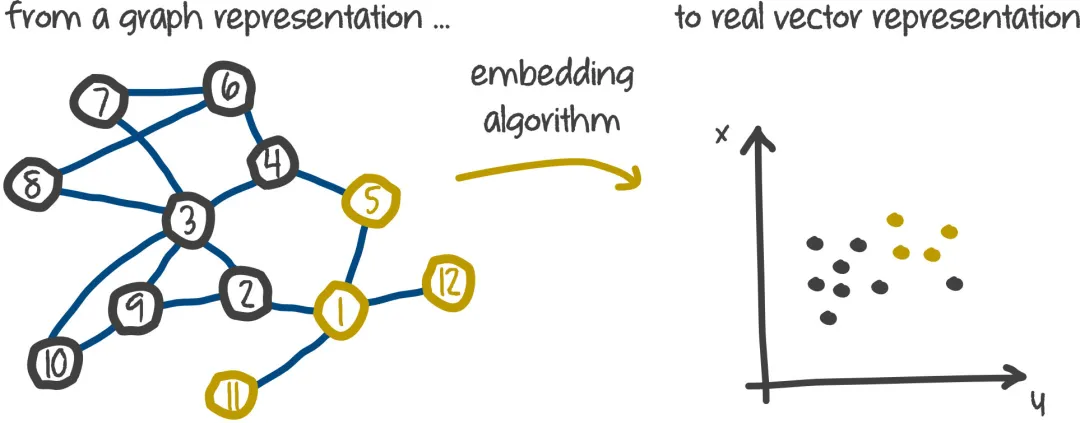
Embedding 作为深度学习的热门研究方向,经历了从序列样本、理图样本、再到异构的多特征样本的发展过程。此外,由于 embedding 技术本身具有较强的综合信息表示能力、较低的上线部署门槛,进一步加速了其在工业上的落地。
Embedding 对于推荐系统中深度学习方法的主要应用可以简单总结如下:
- 作为 Embedding 层嵌入到深度模型中,实现将高维稀疏特征到低维稠密特征的转换(如 Wide&Deep、DeepFM 等模型);
- 作为预训练的 Embedding 特征向量,与其他特征向量拼接后,一同作为深度学习模型输入进行训练(如 FNN);
- 在召回层中,通过计算用户和物品的 Embedding 向量相似度,作为召回策略(比 Youtube 推荐模型等);
- 实时计算用户和物品的 Embedding 向量,并将其作为实时特征输入到深度学习模型中(比 Airbnb 的 embedding 应用)。
对于推荐场景中,什么数据可以采用 Embedding 来构造特征呢?下面简单列了下我在做微信游戏中心场景游戏和内容推荐时主要采用 embedding 技术来处理的数据( 本文只简单列一下主要的点,后续会详细文章来具体讲如何处理以及其带来的效果)。
- User 数据(用户的基础属性数据,如性别、年龄、关系链、兴趣偏好等)
- 对于用户兴趣偏好,一般简单地采用文本 embedding 方法来得到各标签的 embedding 向量,然后根据用户对个标签的偏好程度做向量加权;
- 对于关系链数据(如同玩好友、游戏中心相互关注等),构造用户关系图,然后 采用基于图的 embedding 方法来得到用户的 embedding 向量;
- Item 数据(Item 基本信息数据,如标题、作者、游戏简介、标签等)
- 对于文本、简介和标签等可以采用基于文本的 embedding 方法来在已有语料上预训练模型,然后得到对应的 embedding 向量(如 word2vec 或者 BERT);
- 此外对于有明确关系的(如 item->文本->标签 or 关键词)可以采用对关键词/标签的向量均值来表示 item 的文本向量(这里安利一下 FaceBook 开源的 StarSpace);
- User 行为数据(用户在场景中的行为数据,如点击、互动、下载等)
- 针对用户对 Item 的操作(如点击、互动、下载)构造用户->item+Item 标签体系,构造用户-item-tag 的异构网络,然后可以采用 Metapath2vec 来得到各节点的 embedding 向量;
- 通过记录用户在整个场景访问 item,构造 Item-Item 关系图,然后采用 DeepWalk 算法得到 item 的向量,用来挖掘 Item 间的关系特征;
- 额外数据(外部扩充数据,如用户游戏行为、用户微信其他场景活跃等)
- 标签型(主要是用户在各场景的兴趣偏好):
- 关系链型(如游戏中心好友、游戏内好友、开黑好友)可以采用用户关系构造用户关系图,采用 Graph embedding 方法(如 GraphSAGE)来表示用户抽象特征
当然,这些处理方法只是我个人这一年多的经验,可能有些地方用的并不是很合理, 欢迎大家一起交流。
下面开始本文正文“介绍现在主流的 Embedding 技术”,主要分三大块:
- 经典的矩阵分解方法:这里主要是介绍 SVD 方法
- 基于内容的 embedding 方法:这部分主要涉及到 NLP 相关的文本 embedidng 方法,包括静态向量 embedding(如 word2vec、GloVe 和 FastText)和动态向量 embedding(如 ELMo、GPT 和 BERT)
- 基于 Graph 的 embedding 方法:这部分主要是介绍图数据的 embedding 方法,包括浅层图模型(如 DeepWalk、Node2vec 和 Metapath2vec)和深度图模型(如基于谱的 GCN 和基于空间的 GraphSAGE)
二、经典矩阵分解法
1、奇异值分解
SVD(Singular value decomposition,奇异值分解)是一种矩阵分解的方法,任何矩阵,都可以通过SVD的方法分解成几个矩阵相乘的形式。
X_{m\times n} \approx U_{m\times r} S_{r\times r} V^T_{r\times n}
其中U_{m\times n}和V_{n\times n}是正交矩阵,\sum_{m\times n}是特征值矩阵。
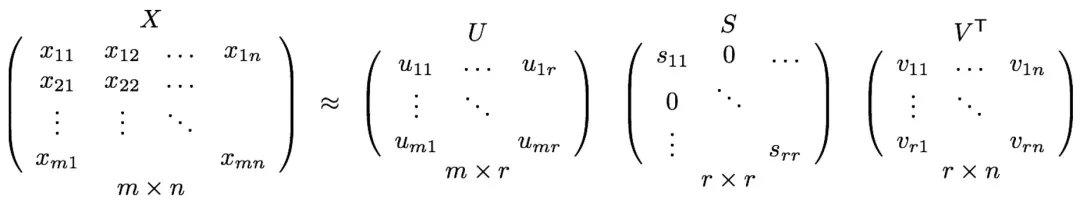
对于机器学习,SVD一个主要优点是对矩阵降维,对于高维矩阵X可以通过SVD表示成三个维度相对较低的矩阵U、S和V。
在推荐系统中,可以将用户行为构造成User-Item的评分矩阵X_{m\times n} ,其中m和n分别表示平台的User数和Item数。 X(i,j)表示用户U_i对物品I_j的评分(也可以是点击、互动、播放、下载等行为),用于刻画User对Item的有效操作。采用SVD算法将M_{m \times n}分解成$U_{m\times r} 、S_{r\times r}和V_{x\times n} ^ T$。
虽然,从形式上看SVD分解简单直接,但由于日常User-Item的评分矩阵事高度稀疏的,而SVD分解要求矩阵是稠密的,通常采用对评分矩阵中的缺失值进行补全(比如补0、全局平均值、用户物品平均值补全等)得到稠密矩阵。再用SVD分解并降维。但实际过程中,元素缺失值是非常多的,导致了传统SVD不论通过以上哪种方法进行补全都是很难在实际应用中起效果。此外传统SVD在实际应用中还有一个严重的问题——计算复杂度(时间复杂度是O(n^3),空间复杂度是O(nmp))。当用户数和物品总量过大(如千上万级),对矩阵做SVD分解是非常耗时。这是得传统的SVD分解方法很难在实际业务中应用起来。
研究者们做了大量工作来解决传统SVD的稀疏数据不适用和高计算复杂度的问题,其中主要的有FunkSVD、BiasSVD和SVD++算法。
2、隐语义模型(Latent Factor Model)
LFM主要代表是2006年由Simon Funk在博客上公开的算法FunkSVD,将评分矩阵分解成两个低维矩阵(P和Q)相乘,可直接通过训练集中的观察值利用最小化均方根学习P,Q矩阵。
X_{m\times n} \approx P_{k\times m}^T Q_{k\times n}
用户u对物品i的评分可以表示为p_u^Tq_i,其中p_u和q_i分别是矩阵P和Q对应第u和i的列向量,表示用户u和物品i的隐向量。FunkSVD核心思想是将在原始SVD上加了线性回归,使得我们可以用均方差作为损失函数来寻找P和Q的最佳值:
L(X,P,Q) = \sum{(X_{u,i}-p_u^Tq_i)^2} = \sum{(X_{u,i} - \sum_{f=1}^kp_{uf}q_{if})^2}
上式可以通过梯度下降法来求解,损失函数求偏导为:
\frac{dL}{dp_{uf}} = -2q_{ik} + 2\lambda p_{uk} \\ \frac{dL}{dq_{if}} = -2p_{uk} + 2\lambda q_{ik}
参数更新如下:
p_{uf} = p_{uf} - \alpha \frac{dL}{dp_{uf}} = p_{uf} + \alpha (q_{ik}-\lambda p_{uk}) \\ q_{if} = q_{if} - \alpha \frac{dL}{dq_{if}} = q_{if} + \alpha (p_{uk}-\lambda q_{ik})
在Funk-SVD获得巨大成功之后,研究人对其进行进一步优化工作,提出了一系列优化算法。其中BiasSVD就是在原始FunkSVD模型中添加三项偏移项优化得到的:
- 物品偏移量 (b_i):表示了物品接受的评分和用户没有多大关系,物品本身质量决定了的偏移;
- 用户偏移量 (b_u):有些用户喜欢打高分,有些用户喜欢打低分,用户决定的偏移;
- 全局偏移量 (\mu):根据全局打分设置的偏移,可能和整体用户群和物品质量有相对应的关系。
BiasSVD的预测结果为:
\hat{X}_{u,v} = \mu + b_u + b_i + p_u^Tq_i
损失函数为:
L = \sum{(X_{u,i}-\hat{X}_{u,i})^2} + \lambda(b_u^2+b_i^2+||p_u||^2 + ||q_i||^2)
SVD++算法是在BiasSVD的基础上引入隐式反馈(如用户历史浏览、用户历史评分、电影历史浏览、电影历史评分等)作为新的参数,其预测结果为:
\hat{X}_{u,i} = \mu + b_u + b_i + q_i^T (p_u + \frac{1}{||X_u||\sum_{j\in X_u}y_j})
其优化如下:
e_{u,i} = X_{u,i} - \hat{X}_{u,i} \\ b_i \leftarrow b_i + \alpha (e_{u,i} - \lambda b_i) \\ b_u \leftarrow b_u + \alpha (e_{u,i} - \lambda b_u) \\ p_u \leftarrow p_u + \alpha (e_{u,i}q_i - \lambda p_u) \\ q_i \leftarrow q_i + \alpha (e_{u,i}(p_u + \frac{1}{||X_u||}\sum_{j\in X_u}{y_j}) - \lambda q_i) \\ y_j \leftarrow y_j + \alpha(e_{u,i}\frac{1}{||R_u||}q_i - \lambda q_i)
虽然矩基于矩阵分解的方法原理简单,容易编程实现,具有较好的扩展性,在小规模数据上也有不错的表现。但对于如今互联网推荐场景的数据量级,矩阵分解方法很难与深度学习算法一战。
三、基于内容的Embedding方法
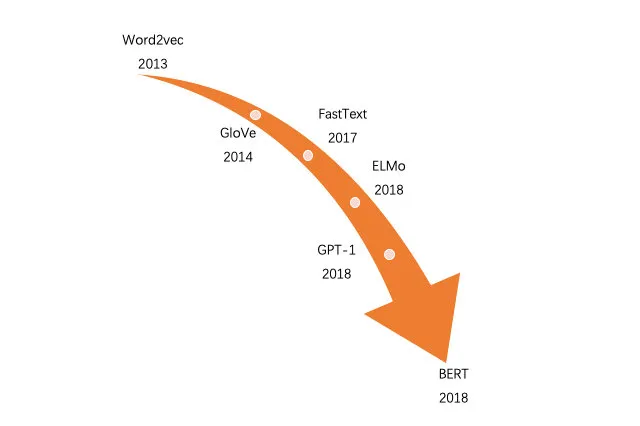
对于基于内容的embedding方法,主要是针对文本类型数据(对图像、音视频等多媒体数据embedding方法,感兴趣的可以自行查阅相关技术)。下图是从word2vec到BERT的发展历史(最新已经发展到了GPT3了,模型更新太快,还没来得及用,就已经过时了),从图中可以看出自从2013年word2vec横空出世后,文本embedding方法不断被优化。从最开始的静态向量方法(如word2vec、GloVe和FastText)发展为能根据上下文语义实现动态向量化的方法如(ELMo、GPT和BERT)。下面主要从分静态向量和动态向量两个方面来介绍相应的方法。
1、静态向量
所谓静态向量指的是一旦训练完成后,对应的向量便不再发生改变,比如一个词经过向量化之后,在后续的场景中该词对应的向量不会发生改变。这些方法主要包括Word2Vec、GloVe和FastText。
A) Word2vec
Word2vec是2013年Google发布的无监督词向embedding模型。该模型采用CBOW或Skip-gram模型来训练词向量,将词从one-hot编码的向量映射成d维稠密向量:
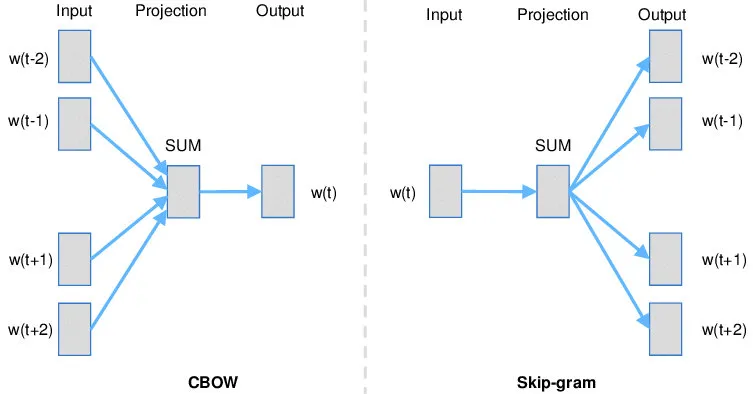 其中CBOW是采用词的上下文来预测该词,而Skip-gram则是采用词来预测其上下文。两者网络结构相似,通常所得到的词向量效果相差不大;但对于大型语料,Skip-gram要优于CBOW。
其中CBOW是采用词的上下文来预测该词,而Skip-gram则是采用词来预测其上下文。两者网络结构相似,通常所得到的词向量效果相差不大;但对于大型语料,Skip-gram要优于CBOW。
B) GloVe
GloVe(Global Vectors for Word Representation)是2014年由斯坦福大学提出的无监督词向量表示学习方法,是一个基于 全局词频统计(count-based & overall statistics)的词表征工具。由它得到的词向量捕捉到单词之间一些语义特性,比如相似性、类比性等。GloVe主要分为三步:
-
基于语料构建词的共现矩阵X
X_{i,j}表示词i和词j在特定大小的窗口内共同出现的次数。如对于语料:
I play cricket, I love cricket and I love football,窗口为2的的共现矩阵可以表示为:
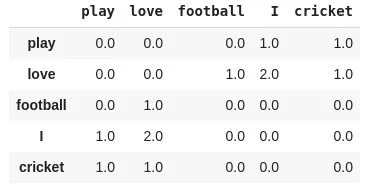
构造词向量和贡献矩阵之间的关系:
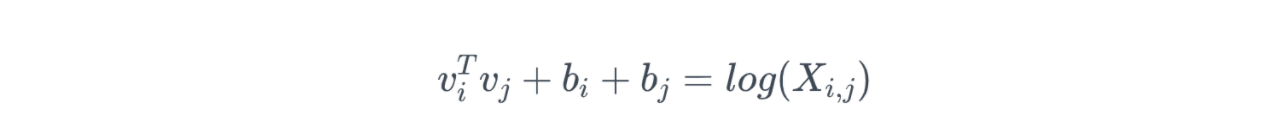
其中,v_i和v_j是要求解的词向量,b_i和b_j是两个词向量的偏差项。
- 最终 GloVe 的 loss function 如下:
J = \sum_{i,j}^N{f(X_{i,j})(v_i^Tv_j + b_i + b_j - log(X_{i,j}))^2}
其中,N表示语料库中词个数。在语料库中,多个单词会一起出现多次,f表示权重函数主要有以下原则:
- 非递减函数,用于确保多次一起出现的单词的权重要大于很少在一起出现的单词的权重
- 权重不能过大,达一定程度之后应该不再增加
- f(0)=0,确保没有一起出现过的单词不参与loss的计算
在论文中,作者给出了如下分段函数:
f(x)= \begin{cases} (x/x_{max})^\alpha & if x < x_{max}\\ 1& if x >= x_{max} \end{cases}
通过实验,作者得到了效果相对较好的\alpha=3/4 ,x_{max}=100,此时对应 曲线如下图:
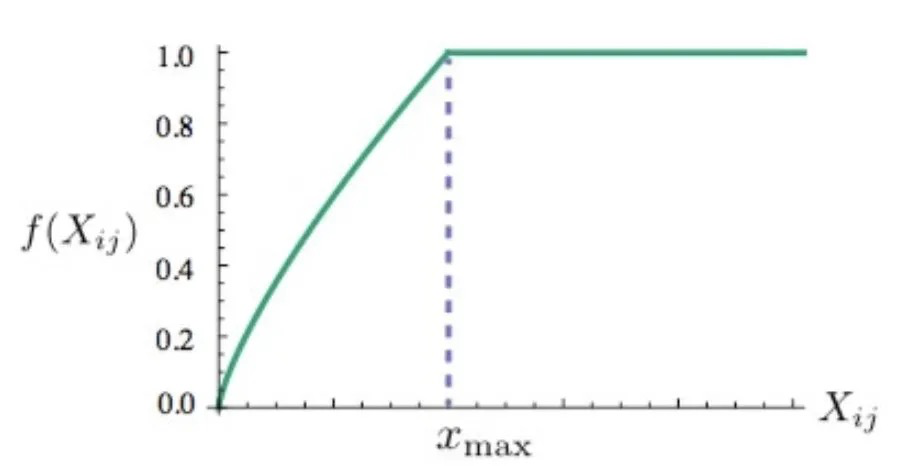
CBOW和Skip-gram是local context window的方法,缺乏了整体的词和词的关系,负样本采样会缺失词的关系信息。此外,直接训练Skip-gram类型的算法,很容造成高曝光词汇得到过多的权重。Global Vector融合了矩阵分解Latent Semantic Analysis (LSA)的全局统计信息和local context window优势。融入全局的先验统计信息,可以加快模型的训练速度,又可以控制词的相对权重。
C) FastText
FastText是FaceBook在2017年提出的文本分类模型(有监督学习)。词向量则是FastText的一个副产物。FastText模型结果如下图所示:
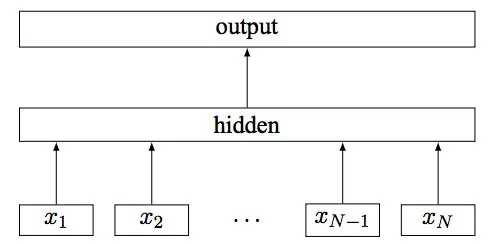
其中x_1, x_2, …,x_{N-1}, x_N表示一个文本中的n-gram向量,每个特征是词向量的平均值。从模型结构可以看出,FastText与CBOW模型的结构相似,不同在于FastText预测的是全部的n-gram去预测指定类别,而CBOW预测的是中间词。
2、动态向量
由于静态向量表示中每个词被表示成一个固定的向量,无法有效解决一词多义的问题。在动态向量表示中,模型不再是向量对应关系,而是一个训练好的模型。在使用时,将文本输入模型中,模型根据上下文来推断每个词对应的意思,从而得到该文本的词向量。在对词进行向量表示时,能结合当前语境对多义词进行理解,实现不同上下文,其向量会有所改变。下面介绍三种主流的动态向量表示模型:ELMo、GPT和BERT。
A) ELMo
ELMo(Embeddings from Language Models)是2018年3月发表,获得了NAACL18的Best Paper。ELMo的模型结构如下图所示:
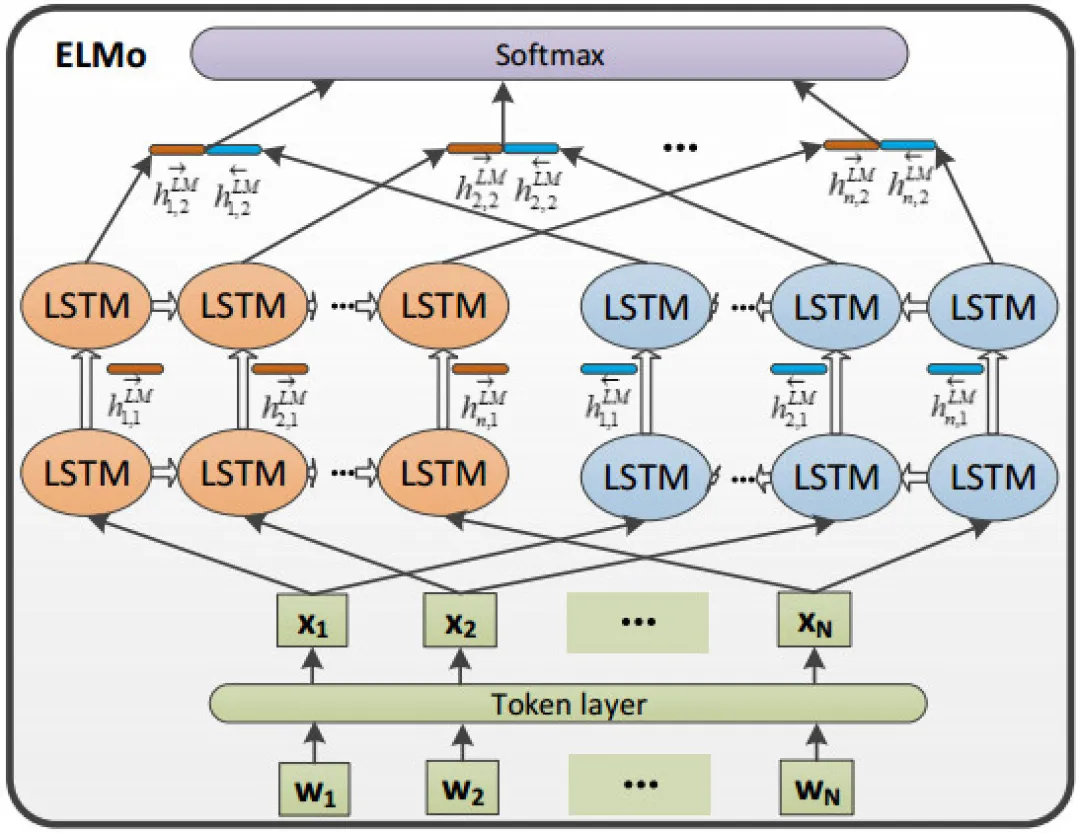
由于当时并没有提出现在火热的Transformer结构,ELMo采用的是多层双向LSTM来搭建模型。在给定一个包含N个token的文本 (t1, t2, ..., tN):
- 前向语言模型用于计算给定句子
t1,t2,...,tk-1,目标为tk的概率:
p(t_1, t_2, …, t_N) = \prod_{k=1}^N{p(t_k|t_1,t_2,…,t_{k-1})}
- 后向语言模型与前向相反,对于给定
tk+1,tk+2,...,tN,目标为tk的概率:
p(t_1, t_2, …, t_N) = \prod_{k=1}^N{p(t_k|t_{k+1},t_{k+2},…,t_N)}
最终目标函数为:
L = \sum_{k=1}^N{log\ p(t_k|t_1,…,t_{k-1}; \Theta_x, \stackrel{\rightarrow}{\Theta}_{LSTM}, \Theta_s) + log \ p(t_k|t_{k+1},…, t_N; \Theta_x, \stackrel{\leftarrow}{\Theta}_{LSTM}, \Theta_s)}
其中,\Theta_x是输入token的embedding,\Theta_s表示softmax层的参数,\stackrel{\rightarrow}{\Theta}_{LSTM}和\stackrel{\leftarrow}{\Theta}_{LSTM}分别是双向LSTM的参数。
对于每个输入的token,一个L层的双向LSTM输出有 2L+1 个向量:
R_k = \{x_k^{LM}, h_{k,j}^{\stackrel{\rightarrow}{LM}}, h_{k,j}^{\stackrel{\leftarrow}{LM}} | j=1,…,L\} = \{h_{k,j}^{LM}| j=0,…,L\}
其中,h_{k,j}^{LM}表示第j层中底k个节点的输出(\stackrel{\rightarrow}{LM}和\stackrel{\leftarrow}{LM}分别表示前向和反向),j=0表示token layer,j>0表示双向LSTM layer。
在下游的任务中, ELMo把所有层的R压缩在一起形成一个向量:
ELMo_k^{task} =E(R_k; \Theta^{task}) = \gamma^{task}\sum_{j=0}^L{s_j^{task} h_{k,j}^{LM}}
具体步骤如下:
- 预训练biLM模型,通常由两层bi-LSTM组成,之间用residual connection连接起来。
- 在任务语料上fine tuning上一步得到的biLM模型,这里可以看做是biLM的domain transfer。
- 利用ELMo提取word embedding,将word embedding作为输入来对任务进行训练。
B) GPT
GPT-1(Generative Pre-Training)是OpenAI在2018年提出的,采用pre-training和fine-tuning的下游统一框架,将预训练和finetune的结构进行了统一,解决了之前两者分离的使用的不确定性(例如ELMo)。此外,GPT使用了Transformer结构克服了LSTM不能捕获远距离信息的缺点。GPT主要分为两个阶段:pre-training和fine-tuning
Pre-training(无监督学习)
预训练模型采用前向Transformer结构如下图所示:
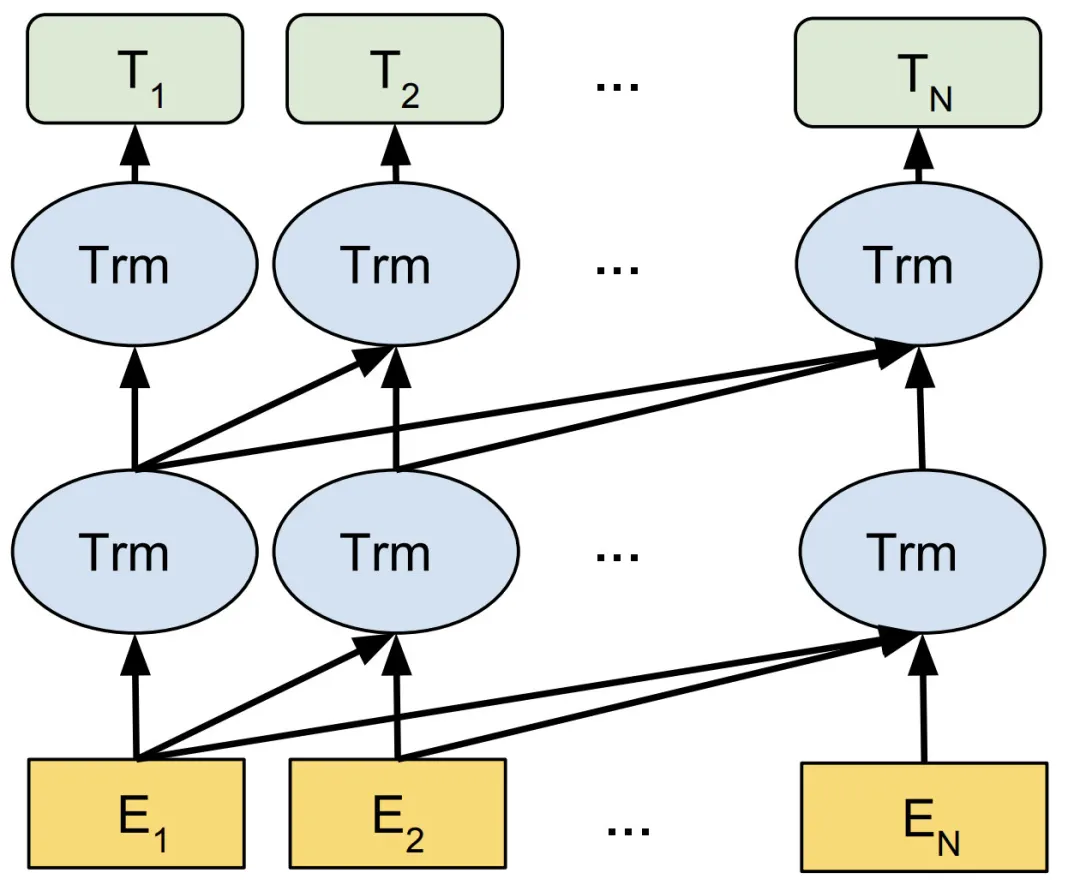 GPT采用auto regressive language model对大量文本进行无监督学习,目标函数就是语言模型最大化语句序列出现的概率,其损失函数为:
GPT采用auto regressive language model对大量文本进行无监督学习,目标函数就是语言模型最大化语句序列出现的概率,其损失函数为:
L_1 = \sum_{i}{log \ P(x_i | x_{i-k},…,x_{i-1}; \Theta)}
其中,k为上文的窗口,P表示参数为\Theta的神经网络模型。
h_0 = U W_e + W_p \\ h_l = transformer(h_{l-1}) \forall i in [1,n] \\ P(u) = softmax(h_nW_e^T)
U表示左侧窗口的上下文词向量,n表示Transformer的层数,W_e表示词向量矩阵,W_p表示position embedding矩阵(作者对position embedding矩阵进行随机初始化并训练学习)。
Fine-tuning(有监督学习)
采用无监督学习预训练好模型后后,可以把模型模型迁移到新的任务中,并根据新任务来调整模型的参数。
假设数据集的一个样本为(x_1, x_2, …, x_m, y),则将(x_1, x_2, …, x_m)输入到预训练好的模型中,得到文本的embedding向量h_l^m,最后采用线性层和softmax来预测标签,输出和损失分别为:
P(y|x_1,x_2, …, x_m) = softmax(h_l^m W_y) \\ L_2 = \sum_{(x,y)}{log \ P(y|x_1,x_2, …,x_m)}
其中,W_y为下游任务的参数。
为避免在Fine-Tuning时,模型陷入过拟合和加速收敛,添加了辅助训练目标的方法,就是在使用最后一个词的预测结果进行监督学习的同时,前面的词继续上一步的无监督训练。最终的损失函数为:
L = L_2 + \lambda L_1
其中,\lambda用于控制无监督目标权重,一般取$0.5$。
总体来说,Fine-tuning阶段需要的额外参数是W_y和以隔符token的embedding。其他任务迁移的输入格式可参考下张图:
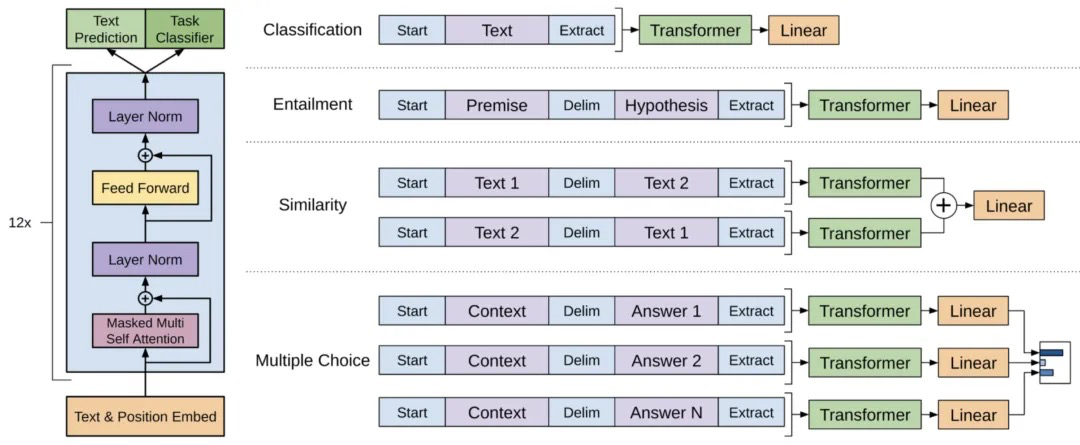
C) BERT
BERT (Bidirectional Encoder Representations from Transformers)是Goole在2018年10月发表的,当时刷新了11项NLP任务,从此成为NLP领域“最靓的仔”。BERT、ELMo和GPT模型结构对比图如下图所示:
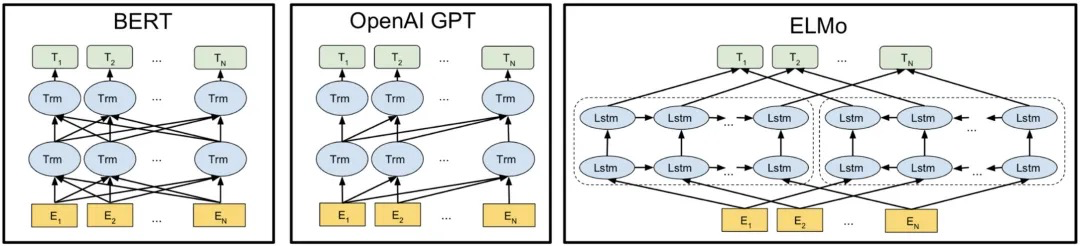
相较于ELMo,BERT采用句子级负采样来得到句子表示/句对关系,使用Transformer模型代替LSTM,提升模型表达能力,Masked LM解决“自己看到自己”的问题。相较于GPT,BERT采用了双向的Transformer,使得模型能够挖掘左右两侧的语境。此外,BERT进一步增强了词向的型泛化能力,充分描述字符级、词级、句子级甚至句间的关系特征。
BERT的输入的编码向量(长度为512)是3种Embedding特征element-wise和,如下图所示:
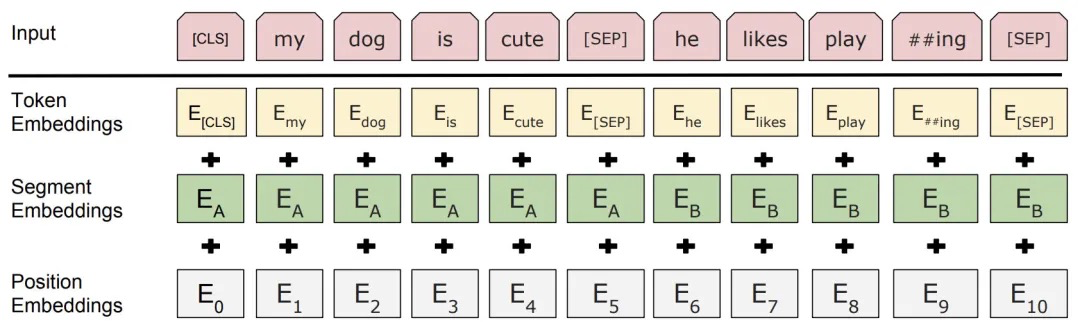
这三种Embedding特征分别是:
- Token Embedding (WordPiece):将单词划分成一组有限的公共词单元,能在单词的有效性和字符的灵活性之间取得一个折中的平衡。如图中的“playing”被拆分成了“play”和“ing”;
- Segment Embedding:用于区分两个句子,如B是否是A的下文(对话场景,问答场景等)。对于句子对,第一个句子的特征值是0,第二个句子的特征值是1;
- Position Embedding:将单词的位置信息编码成特征向量,Position embedding能有效将单词的位置关系引入到模型中,提升模型对句子理解能力;
最后, [CLS] 表示该特征用于分类模型,对非分类模型,该符合可以省去。 [SEP] 表示分句符号,用于断开输入语料中的两个句子。
在模型预训练阶段,BERT采用两个自监督任务采用来实现模型的多任务训练:1)Masked Language Model;2)Next Sentence Prediction
Masked Language Model (MLM)
MLM的核心思想早在1953年就被Wilson Taylor[Wilson]提出,是指在训练时随机从输入语料中mask掉一些单,然后通过该词上下文来预测它(非常像让模型来做完形填空),如下图所以:
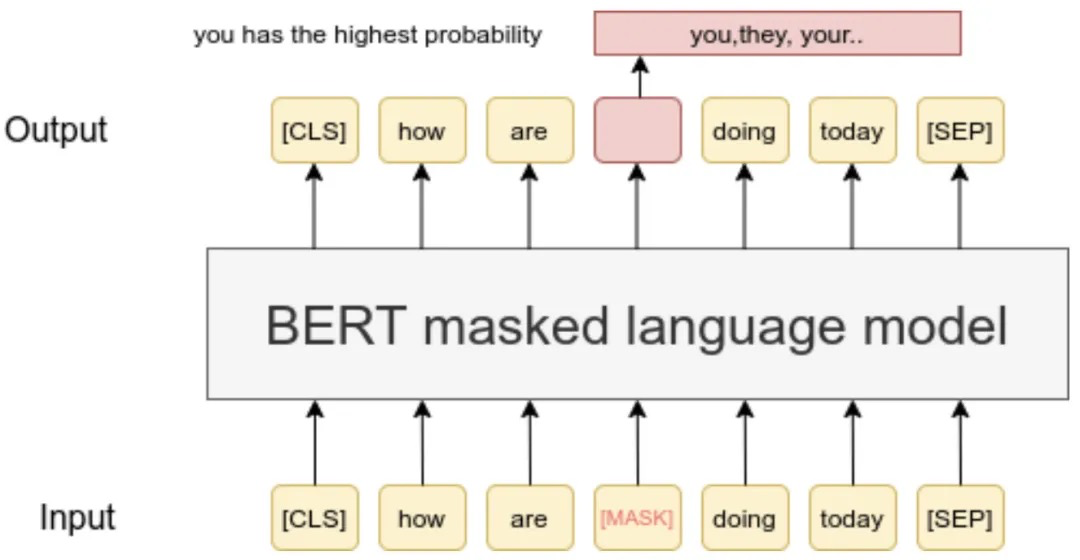
在论文实验中,只有15%的Token会被随机Mask掉。在训练模型时,一个句子会被多次输入模型中用于参数调优,对于某个要被Mask的Token并不是每次都一定会被Mask掉:
80%概率直接替换为[MASK],如my dog is hairy -> my dog is [mask]10%概率替换为其他任意Token,如my dog is hairy -> my dog is appl10%概率保留为原始Token,如my dog is hairy -> my dog is hairy
这样做的好处主要有:
- 如果某个Token100%被mask掉,在fine-tuning的时候会这些被mask掉的Token就成为OOV,反而影响模型的泛化性;
- 加入随机Token是因为Transformer要保持对每个输入Token的分布式表征,否则模型就会记住这个[MASK]=“hairy”
- 虽然加入随机单词带来的负面影响,但由于单词被随机替换掉的概率只有15%*10% =1.5%,负面影响可以忽略不计
Next Sentence Prediction (NSP)
许多重要的下游任务譬如QA、NLI需要语言模型理解两个句子之间的关系,而传统的语言模型在训练的过程没有考虑句对关系的学习。BERT采用NSP任务来增强模型对句子关系的理解,即给出两个句子A、B,模型预测B是否是A的下一句,如下图所示:
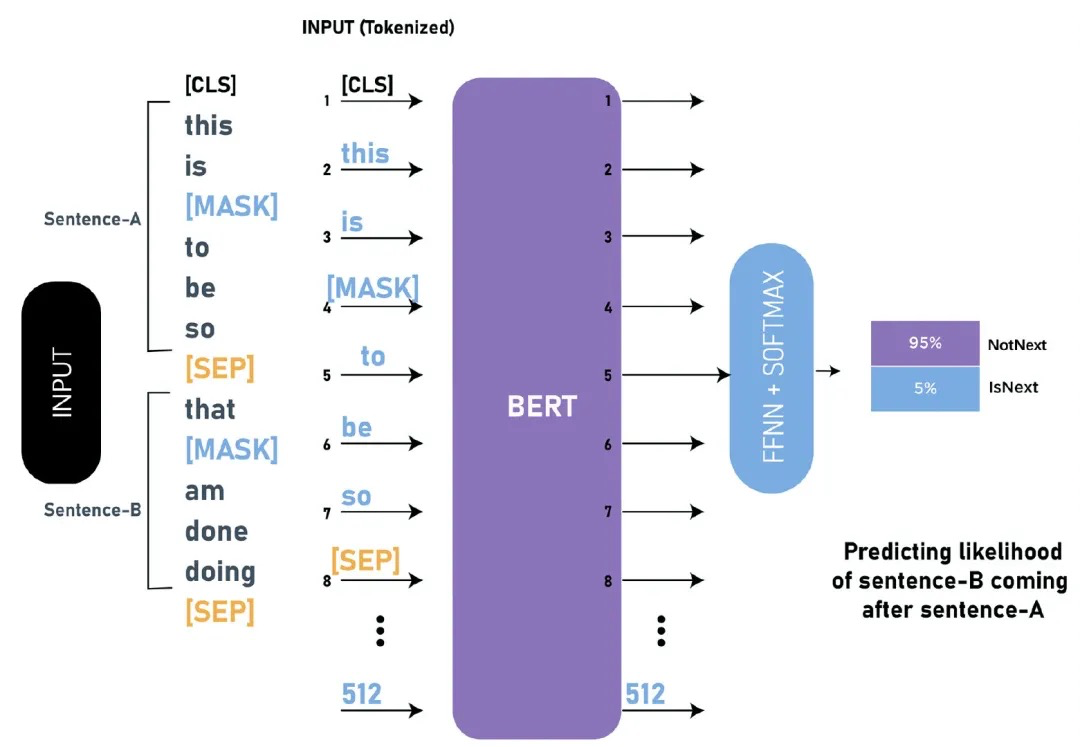
训练数据集构造上,从平行语料中随机抽取连续的两句话:50%保留抽取的两句话(label=IsNext);50%的第二句话随机从语料中抽取(label=NotNext)
Fine-tuning
在 https://github.com/google-research/bert.git 中有N多种预训练模型,大家可以根据需要下载对应的模型,下面主要给出两个常用的模型:
- BERT-Base_L-12_H-768_A-12,总参数为110M
- BERT-Large_L-24_H-1024_A-16,总参数为340M
其中,L表示网络层数(Transformer blocks数量),A表示Multi-Head Attention中self-Attention数,filter的尺寸是4H
BERT提供了4中不同的下游任务的微调方案,大家根据自己的语料在预训练好的模型上采用这些任务来微调模型:
- 句对关系判断:第一个起始符号[CLS]经过编码后,增加Softmax层,即可用于分类;
- 单句分类任务:实现同“句对关系判断”;
- 问答类任务:问答系统输入文本序列的question和包含answer的段落,并在序列中标记answer,让BERT模型学习标记answer开始和结束的向量来训练模型;
- 序列标准任务:识别系统输入标记好实体类别(人、组织、位置、其他无名实体)文本序列进行微调训练,识别实体类别时,将序列的每个Token向量送到预测NER标签的分类层进行识别。
BERT是截止至2018年10月的最新的的SOTA模型,通过预训练和精调可以解决11项NLP的任务。采用Transformer作为算法的主框架,能更好地捕捉更长距离的依赖和语句中的双向关系。与之前的预训练模型相比,BERT能捕捉到正意义上的bidirectional context信息。采用MLP+NSP多任务方法使模型具有更强的泛化能力。最后,强大的计算资源+更大的数据造就了更强更复杂的模型。
四、基于Graph的Embedding方法
基于内容的Embedding方法(如word2vec、BERT等)都是针对“序列”样本(如句子、用户行为序列)设计的,但在互联网场景下,数据对象之间更多呈现出图结构,如1)有用户行为数据生成的物品关系图;2)有属性和实体组成的只是图谱。
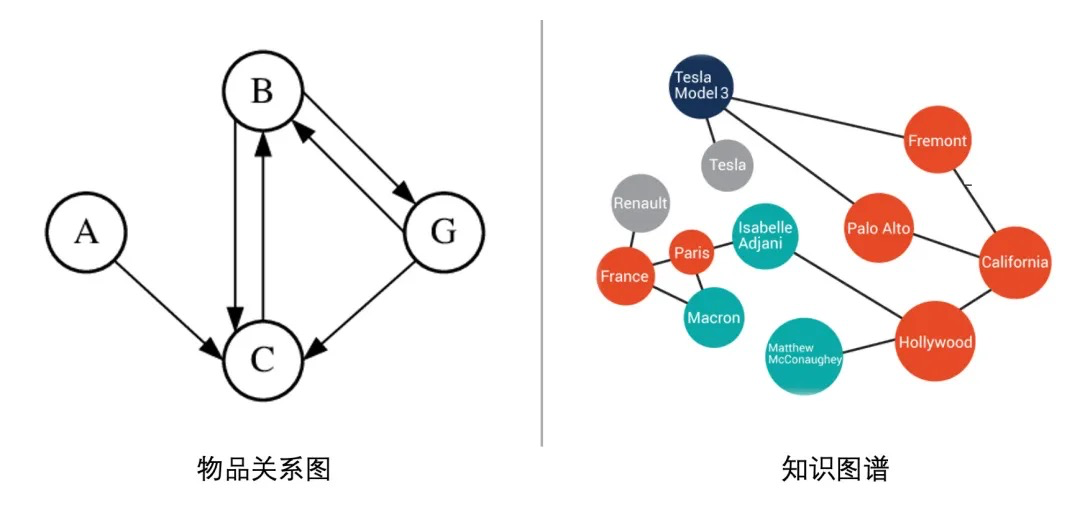
对于图结构数据,基于内容的embedding方法不太好直接处理了。因此,为了解决土结构数据的问题,Graph Embedding开始得到大家的重视,并在推荐系统领域流行起来。
Graph Embedding是一种将图结构数据映射为低微稠密向量的过程,从而捕捉到图的拓扑结构、顶点与顶点的关系、以及其他的信息。目前,Graph Embedding方法大致可以分为两大类:1)浅层图模型;2)深度图模型。
1、浅层图模型
浅层图模型主要是采用 random-walk + skip-gram 模式的embedding方法。主要是通过在图中采用随机游走策略来生成多条节点列表,然后将每个列表相当于含有多个单词(图中的节点)的句子,再用skip-gram模型来训练每个节点的向量。这些方法主要包括DeepWalk、Node2vec、Metapath2vec等。
A) DeepWalk
DeepWalk是第一个将NLP中的思想用在Graph Embedding上的算法,输入是一张图,输出是网络中节点的向量表示,使得图中两个点共有的邻居节点(或者高阶邻近点)越多,则对应的两个向量之间的距离就越近。
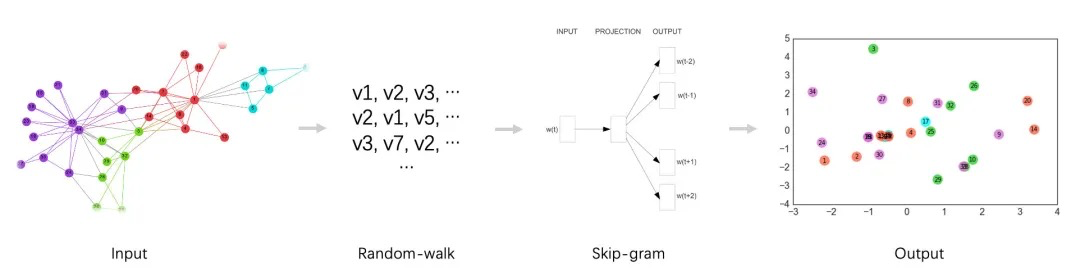
DeepWalk得本质可以认为是: random walk + skip-gram。在DeepWalk算法中,需要形式化定义的是random walk的跳转概率,即到达节点v_i后,下一步遍历其邻居节点v_j的概率:
P(v_j|v_i) = \begin{cases} \frac{M_{ij}}{\sum_{k\in N{+}(v_i)}{M_{ik}}} & ,v_j \in N_{+}(v_i) \\ 0 & ,v_j \notin N_{+}(v_i) \end{cases}
其中,N_{+}(v_i)表示及节点v_i的所有出边连接的节点集合,M_{ij}表示由节点v_i连接至节点v_j的边的权重。由此可见,原始DeepWalk算法的跳转概率是跳转边的权重占所有相关出边权重之和的比例。算法具体步骤如下图所示:

DeepWalk算法原理简单,在网络标注顶点很少的情况也能得到比较好的效果,且具有较好的可扩展性,能够适应网络的变化。但由于DeepWalk采用的游走策略过于简单(BFS),无法有效表征图的节点的结构信息。
B) Node2vec
为了克服DeepWalk模型的random walk策略相对简单的问题,斯坦福大学的研究人员在2016年提出了Node2vec模型。该模型通过调整random walk权重的方法使得节点的embedding向量更倾向于体现网络的同质性或结构性。
- 同质性:指得是距离相近的节点的embedding向量应近似,如下图中,与节点u相连的节点s_1、s_2、s_3 和 s_4的embedding向量应相似。为了使embedding向量能够表达网络的同质性,需要让随机游走更倾向于DFS,因为DFS更有可能通过多次跳转,到达远方的节点上,使游走序列集中在一个较大的集合内部,使得在一个集合内部的节点具有更高的相似性,从而表达图的同质性。
- 结构性:结构相似的节点的embedding向量应近似,如下图中,与节点u结构相似的节点s_6的embedding向量应相似。为了表达结构性,需要随机游走更倾向于BFS,因为BFS会更多的在当前节点的邻域中游走,相当于对当前节点的网络结构进行扫描,从而使得embedding向量能刻画节点邻域的结构信息。
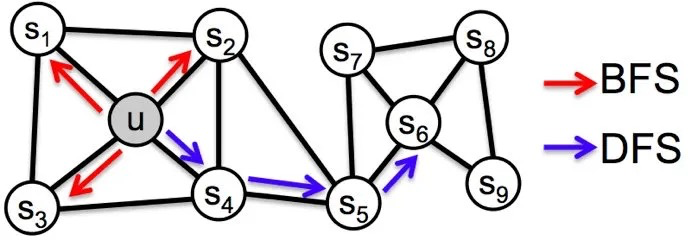
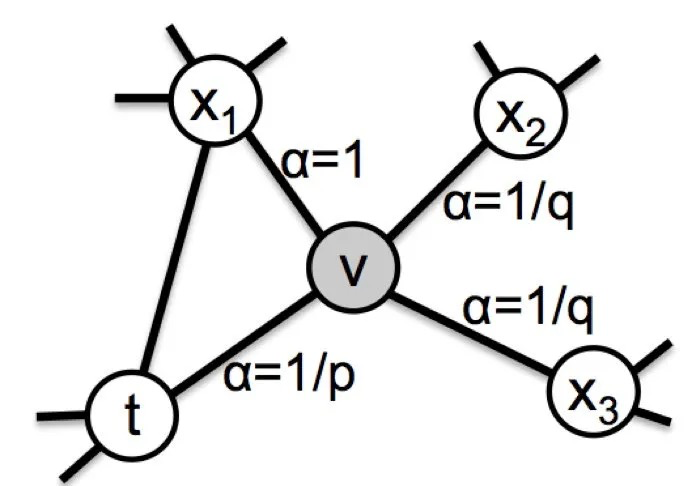
在Node2vec中,同样是通过控制节点间的跳转概率来控制BFS和DFS倾向性的。如下图所示,当算法先由节点t跳转到节点v,准备从节点v跳转至下一个节点时(即t-> v -> x? ),各节点概率定义如下:
\pi_{vx} = \alpha_{p,q}(t,x) \cdot w_{vx}
其中,w_{vx}是节点v和x边的权重,\alpha_{p,q}(t,x)定义如下:
\\ \alpha(t, x) = \begin{cases} \frac{1}{p} & if \ d_{tx} = 0 \\ 1 & if \ d_{tx} = 1 \\ \frac{1}{q} & if \ d_{tx} = 2 \end{cases}
这里d_{tx}表示节点t与x的最短路径,如t与x_1的最短路径为1(即d_{tx_1} = 1),则\alpha_{p,q}(t, x_1)=1。作者引入了两个参数p和q来控制游走算法的BFS和DFS倾向性:
- return parameter p:值越小,随机游走回到节点的概率越大,最终算法更注重表达网络的结构性
- In-out parameter q:值越小,随机游走到远方节点的概率越大,算法更注重表达网络的同质性
当p=q=1时,Node2vec退化成了DeepWalk算法。
下图是作者通过调整p和q,使embedding向量更倾向于表达同质性和结构性的可视化结果:
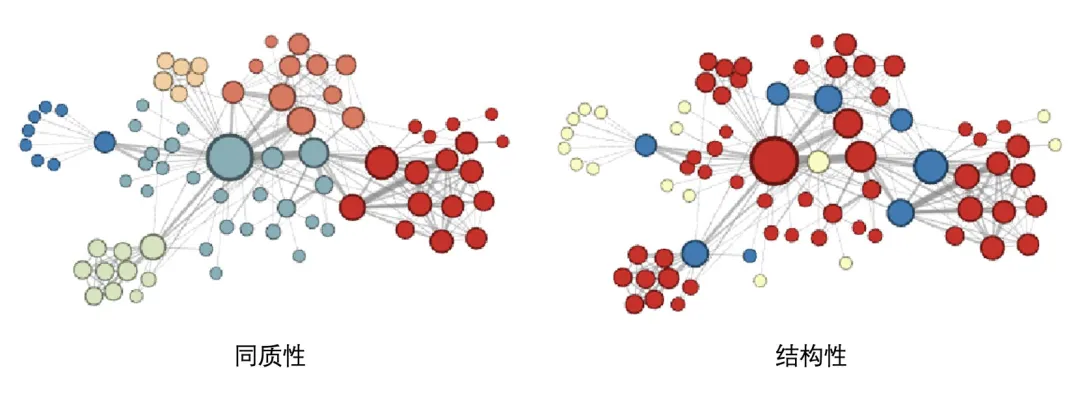
从图中可以看出,同质性倾向使相邻的节点相似性更高,而结构性相似使得结构相似的节点具有更高的相似性。Node2vec的算法步骤如下:

相较于DeepWalk,Node2vec通过设计biased-random walk策略,能对图中节点的结构相似性和同质性进行权衡,使模型更加灵活。但与DeepWalk一样,Node2vec无法指定游走路径,且仅适用于解决只包含一种类型节点的同构网络,无法有效表示包含多种类型节点和边类型的复杂网络。
C) Metapath2vec
为了解决Node2vec和DeepWalk无法指定游走路径、处理异构网络的问题,Yuxiao Dong等人在2017年提出了Metapath2vec方法,用于对异构信息网络(Heterogeneous Information Network, HIN)的节点进行embedding。
Metapath2vec总体思想跟Node2vec和DeepWalk相似,主要是在随机游走上使用基于meta-path的random walk来构建节点序列,然后用Skip-gram模型来完成顶点的Embedding。
作者首先给出了异构网络(Heterogeneous Network)的定义:
异构网络G=(V,E,T),其中节点和边的映射函数分别为\phi(v): v \rightarrow T_v 和 \varphi(e): \\E\rightarrow T_E,满足|T_V|+|T_E|>2,其中V_E和T_E分别是节点和边的类型
即,存在多种类型节点或边的网络为异构网络。
虽然节点类型不同,但是不同类型的节点会映射到同一个特征空间。由于异构性的存在,传统的基于同构网络的节点向量化方法很难有效地直接应用在异构网络上。
为了解决这个问题,作者提出了meta-path-based random walk:通过不同meta-path scheme来捕获不同类型节点之间语义和结构关系。meta-path scheme定义如下:
V_1 \stackrel{R_1}{\rightarrow} V_2 \stackrel{R_2}{\rightarrow} … V_t \stackrel{R_t}{\rightarrow}V_{t+1}…V_{l-1} \stackrel{R_{l-1}}{\rightarrow}V_l
其中R_i表示不同类型节点V_i和V_{i+1}之间的关系。节点的跳转概率为:
p(v^{i+1}|v_t^i,P)=\left\{ \begin{array}{rcl} \frac{1}{|N_{t+1}(v_t^i)|} & if \ (v^{i+1}, v^i_t) \in E \ \& \ \phi(v^{i+1})=t+1\\ 0 & if \ (v^{i+1}, v^i_t) \in E \ \& \ \phi(v^{i+1}) \neq t+1\\ 0 & if \ (v^{i+1}, v^i_t) \notin E \end{array} \right.
其中,v_t^i \in V_t,N_{t+1}(v_t^i)表示节点的类型的邻居节点集合。me ta-path的定义一般是对称的,比如 user-item-tag-item-user。最后采用skip-gram来训练节点的embedding向量:
O = \mathop{\arg \max}_{\theta} \sum_{v\in V}{\sum_{t \in T_v}{\sum_{{c_t}\in N_t(v)}{log \ p(c_t | v; \theta)}}}
其中:N_t(v)表示节点v的上下文中,类型为t的节点,
p_{metapath2vec}(c_t|v; \theta)=\frac{e^{X_{c_t}\cdot X_v}}{\sum_{u\in V}{e^{X_u \cdot X_v}}}
通过分析metapath2vec目标函数可以发现,该算法仅在游走是考虑了节点的异构行,但在skip-gram训练时却忽略了节点的类型。为此,作者进一步提出了metapath2vec++算法,在skip-gram模型训练时将同类型的节点进行softmax归一化:
p_{metapath2vec++}(c_t|v;\theta)=\frac{e^{X_{c_t}\cdot X_v}}{\sum_{u_t\in V_t}{e^{X_{u_t}\cdot X_v}}}
metaptah2vec和metapath2vec++的skip-gram模型结构如下图所示:
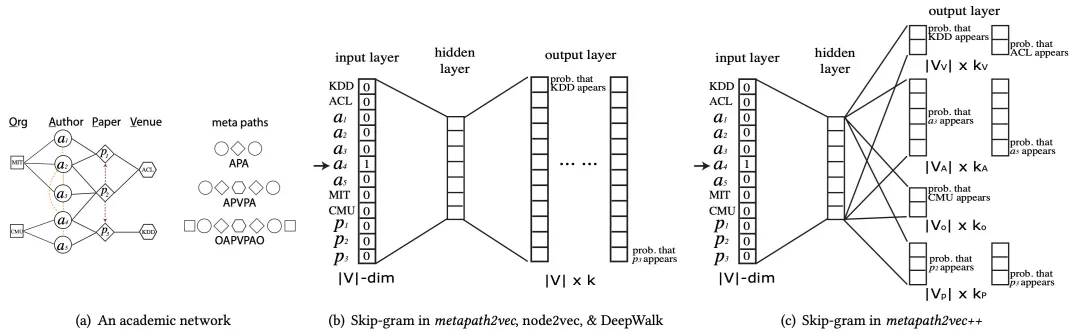
metapath2vec++具体步骤如下图所示:

2、深度图模型
上一节讲的浅层图模型方法在世纪应用中是先根据图的结构学习每个节点的embedding向量,然后再讲得到的embedding向量应用于下游任务重。然而,embedding向量和下游任务是分开学习的,也就是说学得的embedding向量针对下游任务来说不一定是最优的。为了解决这个embedding向量与下游任务的gap,研究人员尝试讲深度图模型是指将图与深度模型结合,实现end-to-end训练模型,从而在图中提取拓扑图的空间特征。主要分为四大类:Graph Convolution Networks (GCN),Graph Attention Networks (GAT),Graph AutoEncoder (GAE)和Graph Generative Networks (GGN)。
本节主要简单介绍GCN中的两个经典算法:1)基于谱的GCN (GCN);2)基于空间的GCN (GraphSAGE)。
其他方法有兴趣的同学可以参考。。。
提取拓扑图的空间特征的方法主要分为两大类:1)基于空间域或顶点域spatial domain(vertex domain)的;2)基于频域或谱域spectral domain的。通俗点解释,空域可以类比到直接在图片的像素点上进行卷积,而频域可以类比到对图片进行傅里叶变换后,再进行卷积。
- 基于 spatial domain:基于空域卷积的方法直接将卷积操作定义在每个结点的连接关系上,跟传统的卷积神经网络中的卷积更相似一些。主要有两个问题:1)按照什么条件去找中心节点的邻居,也就是如何确定receptive field;2)按照什么方式处理包含不同数目邻居的特征。
- 基于 spectral domain:借助卷积定理可以通过定义频谱域上的内积操作来得到空间域图上的卷积操作。
A) GCN
图神经网络的核心工作是对空间域(Spatial Domain)中节点的Embedding进行卷积操作(即聚合邻居Embedding信息),然而Graph和Image数据的差别在于节点邻居个数、次序都是不定的,使得传统用于图像上的CNN模型中的卷积操作不能直接用在图上,因此需要从频谱域(Spectral Domain)上重新定义卷积操作再通过卷积定理转换回空间域上。

Thomas等人在2017年对上式做了进一步简化:限制每个卷积层仅处理一阶邻居特征,通过采用分层传播规则叠加多层卷机,从而实现对多阶邻居特征的传播。通过限制卷机核的一阶近似能缓解节点度分布非常宽的图对局部邻域结构的过度拟合问题。如下图所示,通过集联多个卷积层,节点x_3能聚合多个邻居节点特征。
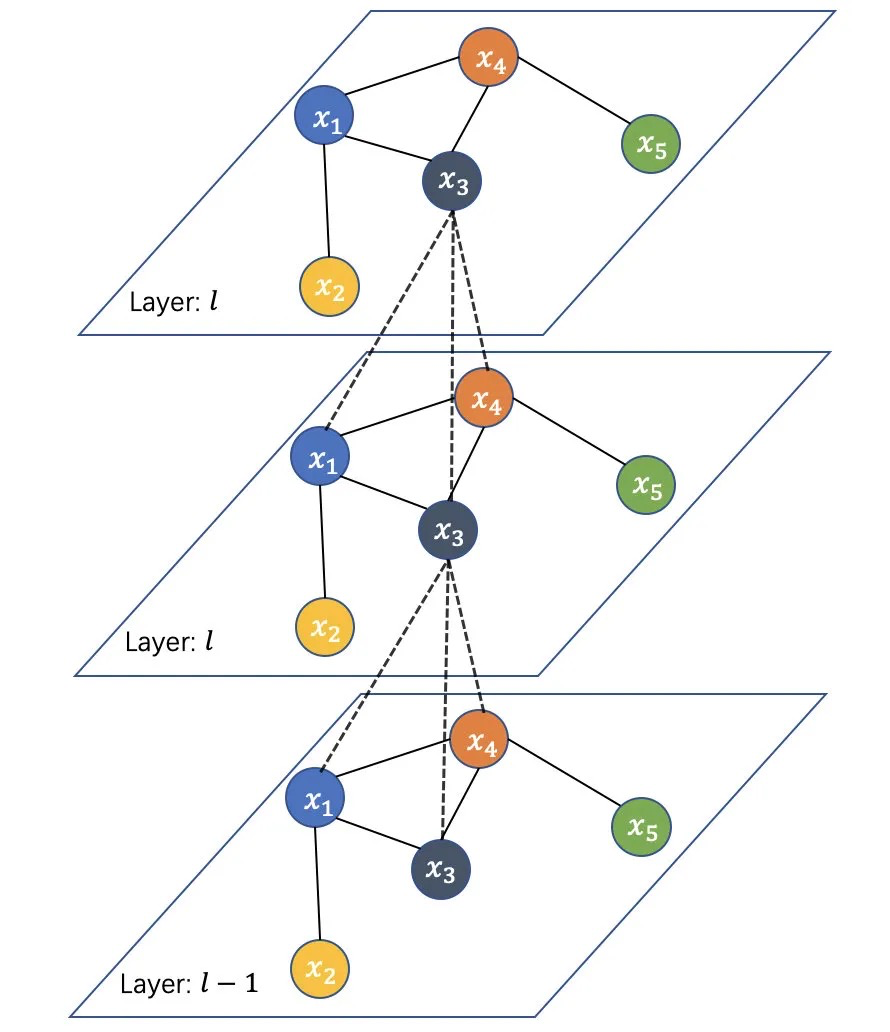
使用切比雪夫一阶展开(K=1)的核卷积+非线性单元如下:
H^{l+1} = \sigma(\widetilde{D}^{-1/2} \widetilde{A} \widetilde{D}^{-1/2} H^{l}W^{l+1})
其中,H^l表示第l层卷积核的输出,作为H^{l+1}的数据,H^0为各节点的特征X。\widetilde{D}^{-1/2} \widetilde{A} \widetilde{D}^{-1/2} 是卷积核的一阶近似,可以简单理解成邻接节点特征的加权平均。\sigma为非线性激活函数,W^l为第l层的卷积核参数(每个节点共享)。
Thomas等人在设计卷积核时做了两个trick:
- 每个节点增加了selp-loop,使在卷积计算时能考虑当前节点自身特征:\widetilde{A}=A + I
- 对\widetilde{A}进行对称归一化:\widetilde{A}=\widetilde{D}^{-1/2} \widetilde{A} \widetilde{D}^{-1/2}。避免了邻接节点数越多,卷积后结果越大的情况。此外这个操作还能考虑邻接节点度大小对卷积核的影响。
B) GraphSAGE
GraphSAGE(Graph SAmple and aggreGatE)是基于空间域方法,其思想与基于频谱域方法相反,是直接在图上定义卷积操作,对空间上相邻的节点上进行运算。其计算流程主要分为三部:
- 对图中每个节点领据节点进行采样
- 根据聚合函数聚合邻居节点信息(特征)
- 得到图中各节点的embedding向量,供下游任务使用
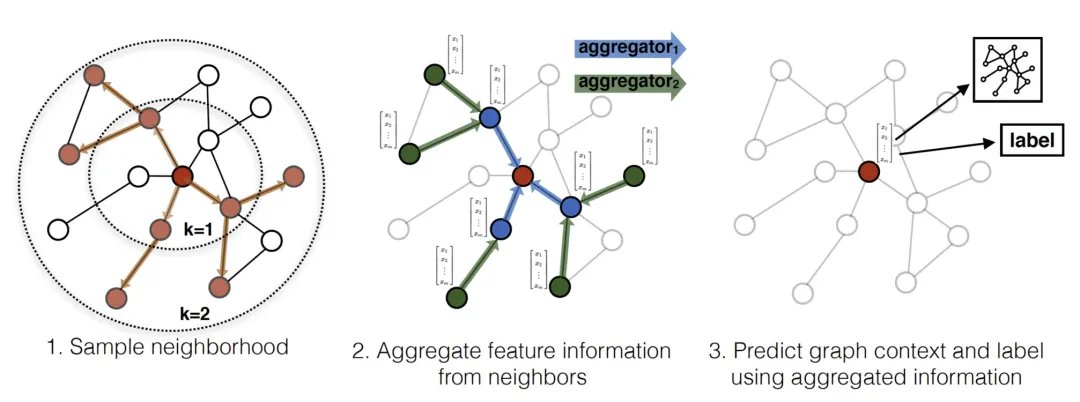
GraphSAGE生成Embedding向量过程如下:

其中 K 表示每个节点能够聚合的邻居节点的跳数(例如 K=2 时,每个顶点可以最多根据其2跳邻居节点的信息来表示自身的embedding向量)。算法直观上是在每次迭代中,节点聚合邻居信息。随着不断迭代,节点得到图中来自越来越远的节点信息。
邻居节点采样:在每个epoch中,均匀地选取固定大小的邻居数目,每次迭代选取不同的均匀样本。
GraphSAGE的损失函数如下:
J_g(z_u) = log(\sigma(z^T_u z_v)) - Q\cdot E_{v_n \sim P_n(v)} log(\sigma(-z_u^Tz_{v_n}))
其中,z_u和z_v表示节点u和v的embedding向量,v是u固定长度的邻居觉点,\sigma是sigmoid函数,P_n和Q分别表示负样本分布和数目。
对于聚合函数的,由于在图中节点的邻居是无序的,聚合函数应是对称的(改变输入节点的顺序,函数的输出结果不变),同时又具有较强的表示能力。主要有如下三大类的聚合函数:
- Mean aggretator:将目标节点和其邻居节点的第k-1层向量拼接起来,然后对计算向量的
element-wis均值,最后通过对均值向量做非线性变换得到目标节点邻居信息表示:
h_v^k \leftarrow \sigma(W \cdot MEAN(\{h_v^{k-1}\} \cup \{h_u^{k-1}, \forall u \in N(v)\}))
- Pooling aggregator:先对目标节点的邻居节点向量做非线性变换并采用pooling操作(maxpooling或meanpooling)得到目标节点的邻居信息表示:
AGGREGATE_k^{pool} = max({\{ \sigma(W_{pool} h_{u_i}^k + b), \forall u_i \in N(v)\}})
- LSTM aggretator:使用LSTM来encode邻居的特征,为了忽略邻居之间的顺序,需要将邻居节点顺序打乱之后输入到LSTM中。LSTM相比简单的求平均和Pooling操作具有更强的表达能力。
五、总结
针对当前热门的embedding技术,本文系统的总结了能处理各类型数据的embedding方法,如传统基于矩阵分解的方法(如SVD分解)、处理文
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/%E4%BA%92%E8%81%94%E7%BD%91/%E8%85%BE%E8%AE%AF%E6%8A%80%E6%9C%AF%E7%94%A8%E4%B8%87%E5%AD%97%E9%95%BF%E6%96%87%E8%81%8A%E4%B8%80%E8%81%8A%E6%8A%80%E6%9C%AF/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


