苏宁仓库内多协作的全局路径规划算法研究
物流仓库如何更好的规划智能叉车?
董效成
2018 年 11 月 1 日
话题:AI算法物联网

本文为『InfoQ x 苏宁 2018 双十一』技术特别策划系列文章之一。
1. 背景
随着物联网和人工智能的发展,越来越多的任务渐渐的被机器人取代,机器人逐渐在发展中慢慢进入物流领域,“智能叉车”,AGV(Automated Guided Vehicle,自主导航车)的出现不仅大大降低了人工成本,还在提升效率,面对海量订单拣选时候有不错的表现。在实际应用中,一个仓库内多个 AGV 协作完成订单是不可或缺的部分,而且多个 AGV 共同运输的过程中同时进行路径规划需要一定的算法做支撑,本文在一个仓库内多个 AGV 协作进行路径规划的方向上进行算法的研究,对其原理和实现进行分析和介绍。
2. 分析
首先,我们的背景设置在物流仓库,针对仓库中常见的入库、拣货、出库等具体的任务细节进行分析,来了解我们 AGV 所面临的场景。
传统的方式一般采用静止的货架,入库时将商品运输到指定货架前,人工上架入库,拣货时人工去到指定的货架拣选订单对应的商品打包出库,引入 AGV 之后,模式将发生改变,我们会在仓库规划指定的入库区、拣选区,AGV 会将包含订单的货架动态地运输到拣选区,排队等待人工或者机械臂拣选到指定的订单拣选筐内打包出库,完成拣选后将货架运输至指定位置。
所以,引入 AGV 之后,我们面临的问题是为了最大限度的提高效率,多个 AGV 如何避免拥堵和碰撞,如何对每个 AGV 规划出更好的行走路线,怎样才能让每个 AGV 花最小的代价,完成更多的任务,将是此文讨论的重点。
3. 问题拆解
要使得多个机器人在道路规划上最优,无非是在单个小车规划路径时考虑其他小车的行驶路线,进而选取最优的一个行驶方案。另外,不同于室外场景,我们在仓库中规划小车路径,整个道路都是可以设计的,所以我们的问题可拆解为:
(1) 仓库中道路的设计;
(2) 获取到其他小车的路径行驶状态;
(3) 定义可能的道路拥堵;
(4) 规划最短路径;
(5) 交通管制。
3.1 仓库中的道路设计
一些常见的道路设计如图 1 和图 2,根据实际的应用场景来布局,考虑的因素包括仓库的结构,商品的种类等,根据实际测试或模拟来选取最优的设计。
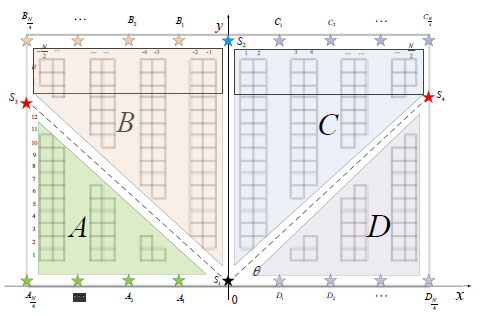
图 1. V 字型道路设计
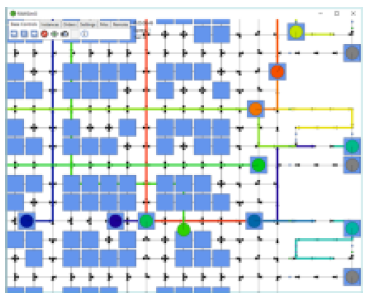
图 2. 井字型道路设计
3.2 获取到其他小车的路径行驶状态
要做到全局路径规划,必须得到每一个时刻小车的位置和运行状态,所以必须和小车建立起稳定的通信系统,一般采用无线局域网的方式,用 TCP 建立连接,选取合适的 WIFI 通道来保证小车和全局路径规划系统的通信的稳健。
3.3 定义可能的道路拥堵
在仓库的道路规划完成之后,首先要考虑的因素是可能的道路拥堵情况,一般小车在仓库中都是直线行走,需要转弯时要停在原地,原地旋转 90°或 180°之后继续直线行走,所以每个转弯都有机会造成当前道路拥堵。另外,同一条道路车流量较大时,也会造成道路拥堵,加上路口会车的情况,主要造成道路拥堵的有转弯、会车和车流量较大 3 种常见的可能情况。
3.4 规划最短路径
最短路径规划是全局路径规划的核心,要从地图上的一个位置到达另一个位置,在中间有障碍物以及考虑到可能的道路拥堵情况,必须使用一个路径搜索算法来寻找从初始点到目标点的一条最短路径,常见的搜索路径的算法有广度优先算法、深度优先算法、Dijkstra 算法、A* 算法等,广度优先算法和深度优先算法适用于树形结构求解最短路径或最小权重的场景,环状结构求解最短路径一般采用 Dijkstra 算法,A* 算法是静态路网中求解最短路径最有效的直接搜索方法。
每一种算法都有其应用场景,对于我们全局路径规划的场景,我们的地图更容易转换成栅格地图,而 A* 算法在栅格地图上搜索最短路径有明显的优势,而且方便于修改加上我们道路拥堵场景的考量,所以我们以 A* 算法为首选最短路径算法,进而分析实现全局路径规划。
3.5 交通管制
交通管制主要应用于会车和并流场景,一方面为了避免车辆碰撞,另一方面路口会车比较常见,处理不好会导致车辆死锁,车辆相互等待,进而导致任务无法完成,也是全局路径规划的核心算法,常见的会车场景如图 3。
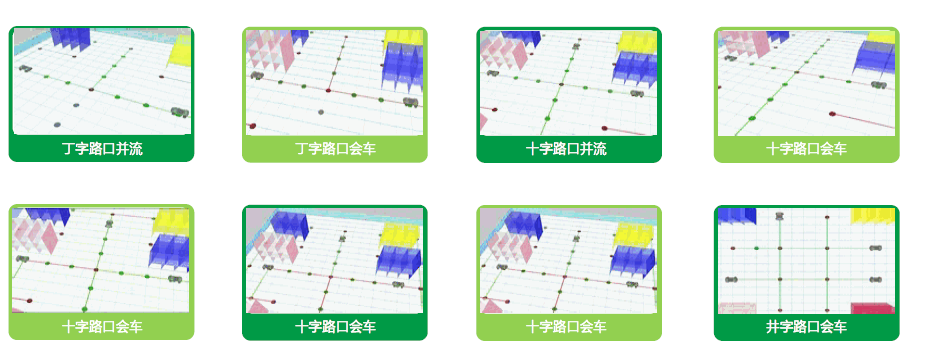
图 3. 路口会车
4. 核心算法实现
路径规划算法的核心主要在于最短路径的规划和交通管制,这里将对一种最短路径规划算法和交通管制算法进行算法剖析,进而设计出一套完整的全局路径规划算法。
4.1 A* 算法规划最短路径
A* 算法类似于图论中寻找最优树,通常是通盘考虑选择某一路径的路径耗费,在所有可通过的路径中总有一条路径相对于其他任何可通行的路径来说是耗费最少的。在图论中寻找最佳路径时每一条的路径耗费是已知且固定的,但在用 A* 算法求解最佳路径时,沿着不同的路径前进,尽管是同一节点但其耗费可能是不同的,这便是启发式寻路的精髓。
运用此方式时,首先将实际问题抽象出来,用矩阵的形式表示问题中的各元素,包括起点位置,目标点位置,以及出现的障碍物。我们会逐渐地发现在寻路方面都是将实际问题抽象地用矩阵表示,之后通过对矩阵的操作模拟实现寻路过程。
其基本思想是以起点为中心,其周围紧邻的 8 个点都通过指针指向它,在其周围点内选择最佳路径点并以它为中心点将其还未建立指针联系的周围点(可行的,这在后文中解释)通过指针指向它,并选择最佳路径点再以此点为中心寻路直到寻找到点的周围点中有目标点,这样寻找的路径就通过指针一一连接起来了,最后通过输出这些点就是寻找的路径了。
下文主要通过以下几个方面来逐步分析 A* 算法的寻路过程:
(1) 将实际问题抽象化为矩阵表示
抽象出的矩阵如图 4,其中绿色区域表示起始点,红色区域表示目标点,中间蓝色区域表示障碍物(如不可通过的高山或是河流),黑色区域表示可产生路径的区域。
(2) 以起点为中心寻找到下一节点
如图 5 所示,以起点为中心与之紧密相邻的 8 个点是其所寻路径上可到的下一点,且都以指针的形式将中间当前点作为与其紧邻的周围点的父节点。对于这 8 个点,应该选择哪一点作为寻路的下一个起点呢,A* 算法中建立了两个列表,一个为开启列表(用于存储所有当前点的可到点(除去已经在关闭列表中的点、障碍物点)),另一个为关闭列表(里面存储已经到过的点,已经在关闭列表中的点在下一次寻路的过程中是不会再次检查的,这也说明寻路的线路不会有相交的可能)。
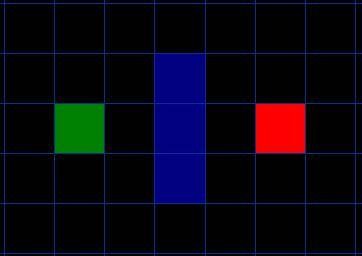
图 4

图 5
(3) 选择下一节点
将起点加入关闭列表,在以后的寻路过程中不再对其进行检查,接下来就是在这 8 个点中选择一个作为下一路径点,选择的原则是在其中寻找路径耗费最小的节点,
其权值用 F 表示,F=G+H
其中 G 表示从起点开始,沿着产生的路径,移动到指定方格上的路径耗费;如图 6 所示,以起点为中心其紧邻周围点有上下左右、对角线方向上的 8 个点,以上下左右移动路径耗费为 10,对角线耗费为 2‾√×102×102×10" role=“presentation” style=“display: inline; font-style: normal; font-weight: normal; line-height: normal; font-size: 16px; text-indent: 0px; text-align: left; text-transform: none; letter-spacing: normal; word-spacing: normal; word-wrap: normal; white-space: nowrap; float: none; direction: ltr; max-width: none; max-height: none; min-width: 0px; min-height: 0px; border: 0px; padding: 0px; margin: 0px; position: relative;">,约为 14。
其中 H 表示从路径所在的当前点到终点的移动路径耗费,计算方法为当前点到目的点之间水平和垂直的方格的数量总和,然后把结果乘以 10。
从图 7 可以看出,起始点右边点的权值 F 最小,故将其作为下一路径点。
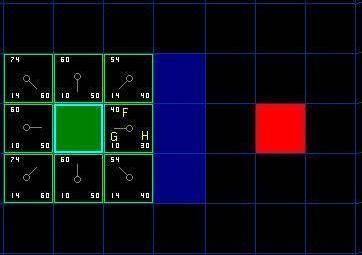
图 6
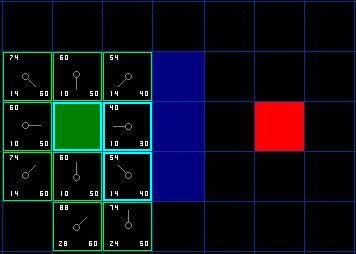
图 7
(4) 继续搜索
把路径点从开启列表中删除,并添加到关闭列表中。检查与此点紧邻的 8 个点(忽略在关闭列表中或者不可通过的点),把他们添加进开启列表,如果存在还有点没有添加进开启列表,则将路径点作为此类点的父节点并添加进开启列表。
如果所有可行的紧邻点已经在开启列表中,对每一紧邻点检查目前这条路径到是否比上一路径点到这一紧邻点的路径耗费要小,如果不是则什么都不用做(如图 8 所示)从原始起点到其紧邻的右下方的点,按照新产生路径 G 值:G1=10+10=20,而原始路径 G 值 G2=14,即新产生路径的 G 值比原始路径的 G 值大,而它们的 H 值相同(为同一点)故原始路径的 F 值比新产生路径的 F 值要小,不做任何处理,继续下一步寻路。如果是,那就把相邻方格的父节点改为目前选中的方格,说明新产生的路径的移动耗费更小。
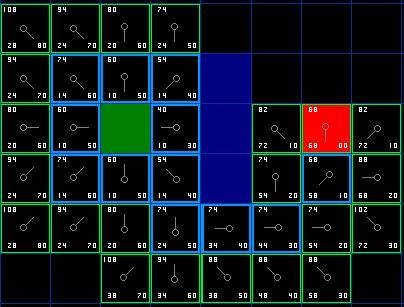
图 8
(5) 重复上一搜索过程直至结束
搜寻过程结束分为两种情况:一种是目标点加入关闭列表,搜索正常结束,找到路径。另一种情况是目标点未找到但开启列表已经为空,意味着没有找到从起始点到目标点的路径,搜索结束。
搜索过程如图 9 所示,从中可以看出从起点到目标点之间有指针指向一致的一条路径,这便 A* 算法是搜寻到的路径。在路径点上添加红色点突出显示,此即为从起始点到终点的一条路径。
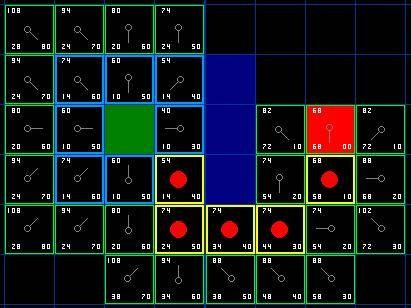
图 9
整个寻路过程整理如下:
-
起始格加入开启列表;
-
重复如下的工作:
a. 寻找开启列表中 F 值最低的点。我们称它为当前点;
b. 把它加入关闭列表;
c. 对紧邻的 8 格中的每一点
- 如果它不可通过或者已经在关闭列表中,略过它。反之如下:
- 如果它不在开启列表中,把它添加进去。把当前点作为这一格的父节点。记录这一点的 F、G 和 H 值;
- 如果它已经在开启列表中,用 G 值为参考检查新的路径是否更好。更低的 G 值意味着更好的路径。如果是这样,就把这一点的父节 点改成当前点,并且重新计算这一点的 G 和 F 值。改变之后需要重新对开启列表按 F 值大小排序。如果不是则不需要做后面改变指针指向并重新计算 G、F 值的工作;
-
停止搜索,分为两种情况:
- 当目标点添加入了关闭列表,这时候路径被找到,搜索正常结束;
- 没有找到目标点,但开启列表已经空了,此时未找到合适的路径,搜索结束;
-
保存路径。从
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/%E4%BA%92%E8%81%94%E7%BD%91/%E8%8B%8F%E5%AE%81%E4%BB%93%E5%BA%93%E5%86%85%E5%A4%9A%E5%8D%8F%E4%BD%9C%E7%9A%84%E5%85%A8%E5%B1%80%E8%B7%AF%E5%BE%84%E8%A7%84%E5%88%92%E7%AE%97%E6%B3%95%E7%A0%94%E7%A9%B6/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


