蘑菇街增量学习番外篇二优化器设计理论篇

作者:美丽联合集团 算法工程师 琦琦 ,
公众号关注:诗品算法
0、引言
在增量学习中,针对不同的模型结构,我们可以设计不同的优化器承接。在这篇文章中,我将为大家详细阐述我们在实践中尝试过的优化器原理及其优缺点。我们最终选择的是AdaDeltaW和FTRL,原因就藏在这篇文章中~相信你会怀揣着对知识的无限渴望读完这篇文章滴~
对增量学习整体框架尚不了解的童鞋,看过来:
蘑菇街首页推荐视频流——增量学习与 wide&deepFM 实践(工程 + 算法)
写这一主题系列的文章实在耗费心(头)血(发),人有三千烦恼丝,而我只剩一千五。。。
1、AdamW的诞生
说到weight decay,大概很多人都耳闻或读过这篇论文——DECOUPLED WEIGHT DECAY REGULARIZATION,从17年底first submit到19年accepted,审稿周期跨越两年。不过它在accepted之前就火 了。
训练神经网络时,AdaGrad、RMSProp、AdaDelta、Adam这种自适应学习率优化器(针对不同参数设置不同学习率的优化算法)得益于优秀的收敛速度,得到了广泛应用。然而,在实际应用中,研究人员更倾向于选择SGD with Momentum,因为Adam模型的泛化性能不如SGD with Momentum。为什么呢?
我们知道,对标准SGD而言,L2 regularization和weight decay是等价的。然而对这种自适应学习率算法来说,这种等价关系还成立吗???作者在文章中指出,导致自适应优化算法泛化性能差的最主要原因就是,Adam中的L2 regularization并不像SGD中的那样有效。 通过将weight decay与梯度更新解耦的方式,可以有效提升Adam的泛化性能。
所以问题来了,weight decay和L2 regularization的具体定义是什么呢?
weight decay是在梯度更新的基础上,对参数

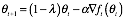 知乎上不方便编辑倒三角符号啊,只能借助于mathType了,有人知道怎么编辑嘛?其中,
知乎上不方便编辑倒三角符号啊,只能借助于mathType了,有人知道怎么编辑嘛?其中,




L2 regularization是在loss function上给参数



对于简单的SGD而言,为了保证L2 reg与wd具有相同效果,L2 reg参数





SGD -> SGDW
作者提出,使用SGD with momentum优化算法,在基于梯度信息更新



 Adam -> AdamW
Adam -> AdamW
对于自适应学习率算法而言,L2 regularization和weight decay之间的区别,就不是简单的超参耦合问题了。加入L2正则时,整体的梯度 = loss function的梯度 + L2正则项的梯度。加入weight decay时,整体梯度 = loss function的梯度(weight decay step与求梯度是分离的)。
在带有L2正则的Adam优化器中,观察Adam的更新公式(下图公式12), 具有较大梯度的权重,其分母中的


实验验证
在上面的部分中,我们已经给出了AdamW(SGDW) 相较于 Adam(SGD)的优势,简单概述为两点,一是超参独立,二是正则有效性对泛化性能的影响。
首先说第一点,超参独立,直接看作者的实验结果,更有说服力。
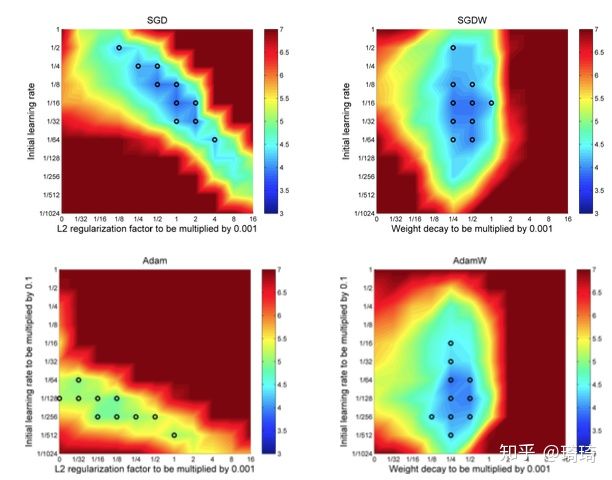
上图中,第一列是带L2 regularization的SGD和Adam,第二列是带weight decay的SGDW和AdamW。在每组结果中,作者用黑色小圈圈绘制的十个点代表十组最优超参。图中的横轴表示L2 regularization或weight decay参数,纵轴表示学习率参数(learning rate)。
- 先观察第一列,在SGD和Adam中,两个超参之间的关系并非垂直于x轴或y轴,而是分布在对角线上。这意味着,两个超参(
)相互依赖,必须同时调整,若仅修改两者中的一个,将会导致结果变差。在SGD中, L2 regularization与初始学习率具有强烈耦合关系,因此调参工程师们认为,SGD的超参设置非常敏感。
- 再观察第二列,带weight decay的SGDW中, weight decay和初始lr参数实现了解耦,两个参数之间的分离度更强了。即使当前的学习率参数未调整到最优值,固定学习率,仅仅优化weight decay因子,也可以获得较优结果。
第二点,正则有效性对泛化性能的影响。
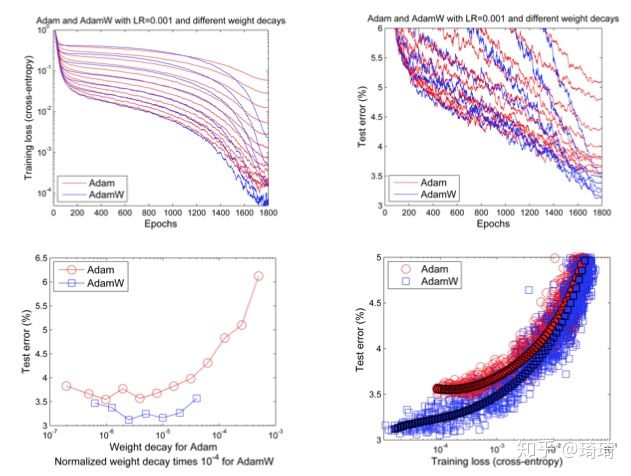
结论很明确,AdamW通常会给模型带来更低的训练loss和测试误差(上图中第一行)。除此之外,在固定相同的训练loss的情况下(上图中第二行),AdamW也有更好的泛化性能。
AdamW与Adam相比,具有更优异的性能。作者在文章末尾也提出,对于其他自适应学习率算法(AdaGrad、RMSProp等)而言,weight decay同样适用。
2、AdaDeltaW的诞生
优化算法经历了 SGD -> SGDM -> AdaGrad -> RMSProp -> AdaDelta -> Adam -> Nadam 这样的发展历程。关于这些算法的细节,网上有很多教程可以参考,在此只说明我们为何pick了AdaDelta。
AdaGrad:你们为什么要抛弃我
AdaGrad算法在训练过程中,一直在累加按元素平方的梯度(更新公式中的分母),自变量中每个元素的学习率在迭代过程中一直在降低(或不变),最终会减小到0,完全停止训练,训练提前终止。 若初始梯度很大,学习率在迭代早期下降较快,在训练的后期阶段,学习率将会很小,较难找到一个有效解。这种情况可以通过增大全局学习率而缓解,使得AdaGrad算法对学习率的选择非常敏感。
Adam:你们为什么要抛弃我
Adam是当前主流的优化算法,是前述算法的集大成者,结合了一阶动量和二阶动量(梯度的一阶和二阶矩)。但也有很多学术界paper怒怼Adam,说它不易收敛,泛化性能差,容易错过全局最优解,越优秀的算法越容易遭人黑吗?可能是期望越大,失望越大?
如此优秀的Adam优化器,在我们场景,泛化性能居然不行,且计算速度不及AdaDelta等优化器。 乐观之人从外界找原因,悲观之人从自身找原因,我正是那种悲观之人,我不喷Adam,只是有点怀疑我这个调参工程师的价值。。。
其实,选哪种优化器,需要在实验中验证,没有一种优化器可以适用于所有场景,玄学至极。去看学术界工业界各种paper,用SGD和Adam的很多,改进版的AdaGrad以及AdaDelta也不少。可能大家把每个算法都试了一遍,哪个效果好,就用哪个。
牛顿法:哼,几乎没人选我
为何业界总是尝试逼近牛顿法,但很少直接用牛顿法呢?牛顿法毕竟收敛快,还带有额外曲率信息呀!但是,牛顿法在计算时,每次参数更新时都将改变参数,因此每轮迭代训练时,都需要计算Hessian矩阵的逆矩阵,计算复杂度非常高。只有参数很少的网络才能使用牛顿法训练,绝大多数神经网络都不可能采用牛顿法训练。而且牛顿法很蠢萌,会主动跳坑里(鞍点)。
AdaDelta:选我选我
我们在增量实践的deep侧优化部分,选择了AdaDeltaW,即AdaDelta + weight decay。
AdaDelta作者指出,这个算法的优秀之处在于,是二阶牛顿法(收敛速度快)的近似。我们知道,牛顿法的迭代公式:



AdaDelta是基于AdaGrad的改进,主要为了解决AdaGrad的两个问题:1)训练过程中,学习率的持续衰减;2)避免手动调节学习率(抢我们的饭碗么不是)。
对应的,AdaDelta的两点改进:
- 使用梯度的指数加权平均替代梯度平方和。 在
时刻,梯度平方累积:
,
是类似于momentum算法中的衰减常数。 参数更新公式变成:
。在这里,
。
- **Hessian矩阵的近似。**觉得这个假设有点牵强。使用Hessian信息的二阶牛顿法或拟牛顿法遵循如下的参数更新方式:
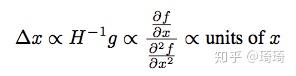 我们可以重新组合牛顿公式如下:
我们可以重新组合牛顿公式如下:
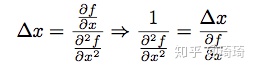 我们来观察AdaDelta最终的更新公式:
我们来观察AdaDelta最终的更新公式:





这些算法的test error对比:
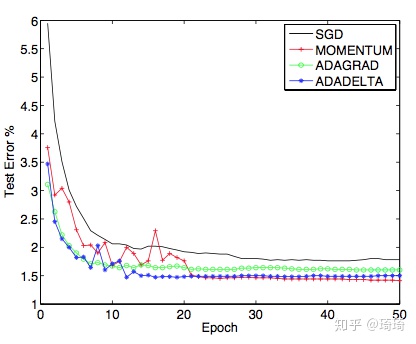
由此可见,AdaDelta算法的设计还是很巧妙的,我们在deep侧,选择了基于weight decay的AdaDelta优化器。
3、FTRL
online learning
常见的梯度下降法、牛顿法、拟牛顿法属于批学习batch方法,每次迭代都需要对全量训练样本重新学习一遍。当搜索推荐的体量高达上亿维度时,传统的batch方法效率太低。online learning在线学习可以解决该问题(我们尚未实现online learning,目前是增量学习)。
最简单的在线学习策略是在线梯度下降:Online Gradient Descent:OGD,即batch_size=1的mini-batch随机梯度下降法的特殊情形。该算法每次迭代时,仅训练最新的样本,每个样本仅被训练一次。在OGD中,算法每次梯度更新并不是沿着全局梯度的负方向前进,带有很大的随机性。即使使用L1正则化,模型也很难产生稀疏解。而在线学习过程中,稀疏性是一个很重要的目标。稀疏解的优点:1)降低特征规模,去除噪声特征,特征选择;2)降低模型大小;3)inference时,计算量大大降低。
FOBOS VS RDA
既然稀疏解是online learning追求的主要目标,因此很多优秀的稀疏优化器应运而生。演化过程:简单截断 -> 梯度截断TG -> FOBOS -> RDA -> FTRL。其中,TG/FOBOS 等算法都是基于随机梯度下降 SGD 算法而来,而正则对偶平均 Regularized Dual Averaging: RDA 算法是基于简单对偶平均法 Simple Dual Averaging Scheme 而来。
L1-FOBOS权重更新公式:
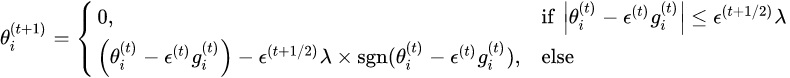 L1-RDA权重更新公式:
L1-RDA权重更新公式:
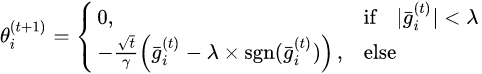 L1-FOBOS和L1-RDA的比较:
L1-FOBOS和L1-RDA的比较:
- L1-FOBOS的截断阈值是随着时间变化的,通常是随着时间下降的。L1-RDA的截断阈值
是固定的常数,因此更加激进,更容易产生稀疏解。
- 截断阈值判定条件:L1-RDA基于梯度的累积均值
来判断,L1-FOBOS基于最近的单次梯度
来判断。梯度累积均值比单次梯度更稳定。
- L1-FOBOS的更新公式中,
由前一时刻的
和
共同决定,而L1-RDA中,
与前一时刻的
无关,仅仅由梯度累积均值 ,商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


