贝壳网两种简单有效的标签选择方法

不论是通过搜索还是推荐,用户看到了很多我们用各种逻辑和理由展示给他的物品,他只从中消费了一部分物品。那么问题来了,到底是那些特性吸引了用户消费呢?
一种简单粗暴的办法是直接把用户产生过行为的物品标签累积在一起。但是这里要说的是另一种思路。
我们把用户对物品的行为,消费或者没有消费看成是一个分类问题,比如点击是“正样本”,“未点击是负样本”。用户用实际行动帮我们标注了若干数据,那么挑选出他实际感兴趣的特性就变成了特征选择问题。
最常用的是两个方法:卡方检验(CHI)和信息增益(IG)。基本思想是:
-
把物品的结构化内容看成文档。
-
把用户对物品的行为看成是类别。
-
每个用户看见过的物品就是一个文本集合。
-
在这个文本集合上使用特征选择算法选出每个用户关心的东西。
CHI
CHI就是卡方检验,本身是一种特征选择方法。
前面的TF-IDF和TextRank都是无监督关键词提取算法,而CHI则是有监督的,需要提供分类标注信息。为什么需要呢?在文本分类任务中,挑选关键词就得为了分类任务服务,而不仅仅是挑选出一种直观上看着重要的词。卡方检验本质上在检验“词和某个类别C相互独立”这个假设是否成立,和这个假设偏离越大,就越说明这个词和类别C有关联,这个词当然就是关键词了。
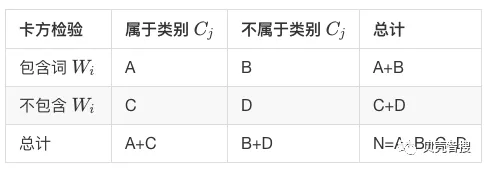
计算一个词 Wi 和一个类别 Cj 的卡方值,需要统计四个值:
-
类别为Cj的文本中出现词 Wi的文本数 A。
-
词 Wi在非Cj的文本中出现的文本数 B 。
-
类别为Cj的文本中没有出现Wi的文本数 C。
-
词 Wi在非Cj的文本中没有出现的文本数 D。
听起来有点绕,我把它画成一个表格更加一目了然。
然后按照如下公式计算每一个词和每一个类别的卡方值:
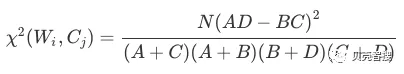
关于这个卡方值计算说明几点:
-
每个词和每个类别都要计算,只要对其中一个类别有帮助的词都应该留下。
-
由于是比较卡方值的大小,所以公式中的N可以不参与计算,因为它对每个词都一样,是总的文本数。
-
卡方值越大,意味着偏离“词和类别相互独立”的假设越远,靠“词和类别互相不独立”这个备择假设越近。
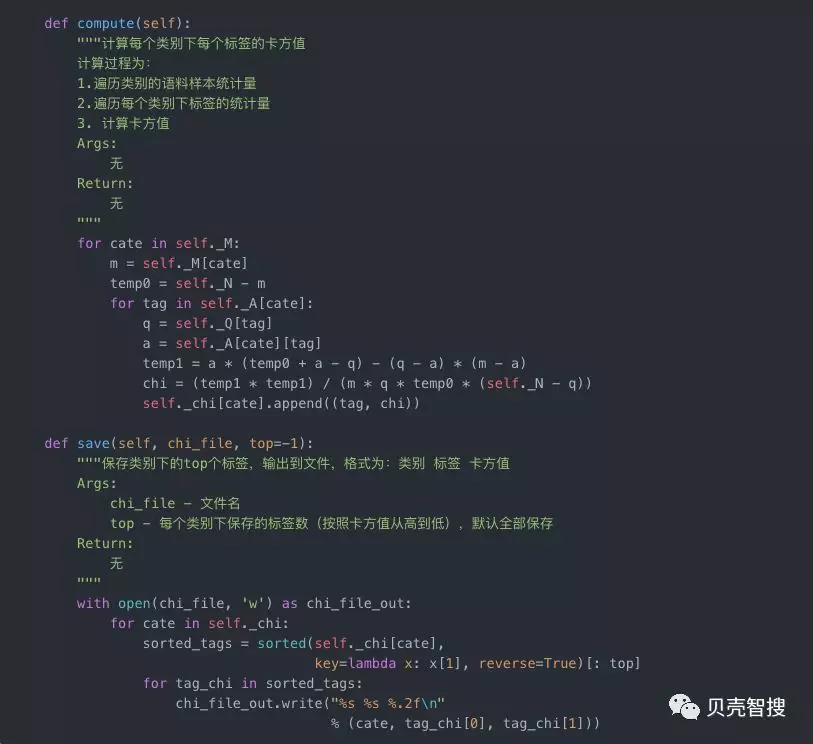
实现卡方算法时候,需要稍微对原公式做一定的变化,降低实现复杂度。观察表格中,有些统计量是不好统计的,比如“不属于类别 C_{j} 且不包含 W_{i}”这个统计量。我们借助另外的统计量来计算卡方值,目的是对语料库一次遍历就得到每个标签的卡方值。
只需要统计这几个量:
-
A:类别Cj中包含词Wi的数量;
-
M: 类别Cj的语料数量,也就是A+C的值;
-
Q:包含词Wi的语料数量,也就是A+B;
-
N:全部语料数量
于是原公式中的B,C,D分别就是:
-
B = Q - A
-
C = M - A
-
D = N + A - Q - M
每个标签与每个类别的卡方值计算方式为:
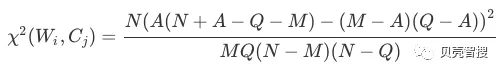
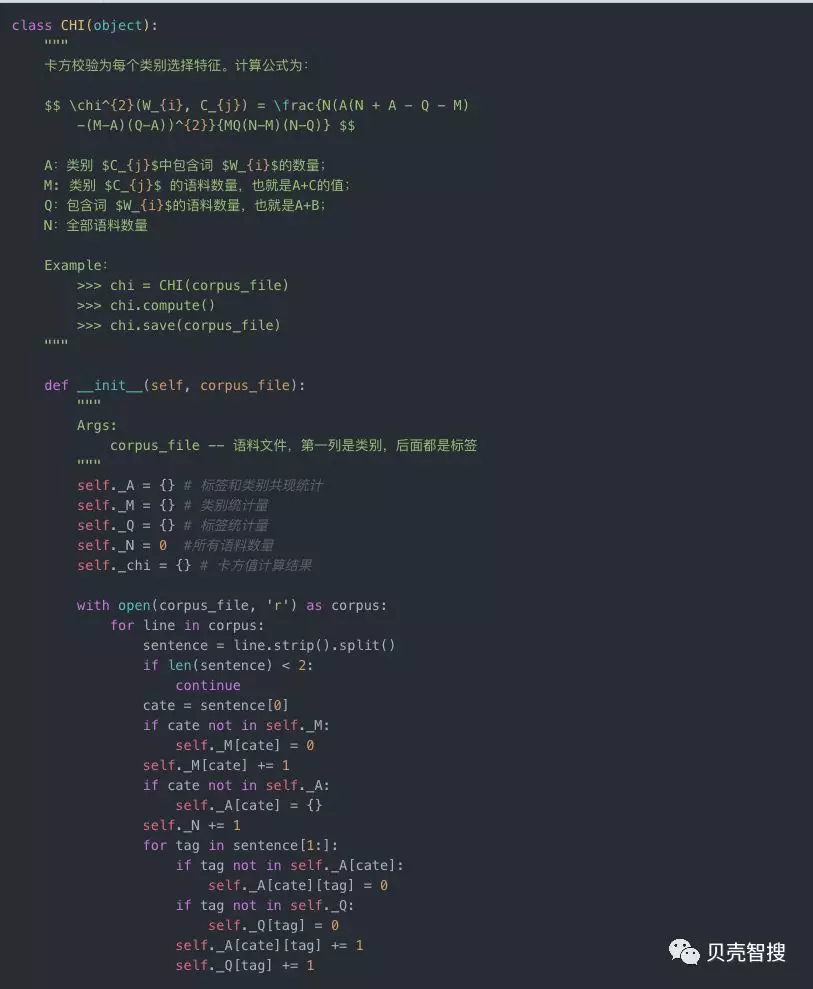
python实现如下:
IG(信息增益)
IG即Information Gain,信息增益,是一种有监督的关键词选择方法,需要有标注信息。要理解信息增益,理解了信息熵就差不多了。
如何理解信息熵?我们还是以上述表格示例说明。一批文本被标注了类别,那么任意挑出一条文本问你,“猜猜这是什么类别?�
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/%E4%BA%92%E8%81%94%E7%BD%91/%E8%B4%9D%E5%A3%B3%E7%BD%91%E4%B8%A4%E7%A7%8D%E7%AE%80%E5%8D%95%E6%9C%89%E6%95%88%E7%9A%84%E6%A0%87%E7%AD%BE%E9%80%89%E6%8B%A9%E6%96%B9%E6%B3%95/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


