推荐系统遇上深度学习一模型理论和实践
原文发布于微信公众号 - 小小挖掘机(wAIsjwj)
原文发表时间:2018-04-10
1、FM背景
在计算广告和推荐系统中,CTR预估(click-through rate)是非常重要的一个环节,判断一个商品的是否进行推荐需要根据CTR预估的点击率来进行。在进行CTR预估时,除了单特征外,往往要对特征进行组合。对于特征组合来说,业界现在通用的做法主要有两大类:FM系列与Tree系列。今天,我们就来讲讲FM算法。
2、one-hot编码带来的问题
FM(Factorization Machine)主要是为了解决数据稀疏的情况下,特征怎样组合的问题。已一个广告分类的问题为例,根据用户与广告位的一些特征,来预测用户是否会点击广告。数据如下:(本例来自美团技术团队分享的paper)
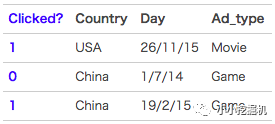
clicked是分类值,表明用户有没有点击该广告。1表示点击,0表示未点击。而country,day,ad_type则是对应的特征。对于这种categorical特征,一般都是进行one-hot编码处理。
将上面的数据进行one-hot编码以后,就变成了下面这样 :

因为是categorical特征,所以经过one-hot编码以后,不可避免的样本的数据就变得很稀疏。举个非常简单的例子,假设淘宝或者京东上的item为100万,如果对item这个维度进行one-hot编码,光这一个维度数据的稀疏度就是百万分之一。由此可见,数据的稀疏性,是我们在实际应用场景中面临的一个非常常见的挑战与问题。
one-hot编码带来的另一个问题是特征空间变大。同样以上面淘宝上的item为例,将item进行one-hot编码以后,样本空间有一个categorical变为了百万维的数值特征,特征空间一下子暴增一百万。所以大厂动不动上亿维度,就是这么来的。
3、对特征进行组合
普通的线性模型,我们都是将各个特征独立考虑的,并没有考虑到特征与特征之间的相互关系。但实际上,大量的特征之间是有关联的。最简单的以电商为例,一般女性用户看化妆品服装之类的广告比较多,而男性更青睐各种球类装备。那很明显,女性这个特征与化妆品类服装类商品有很大的关联性,男性这个特征与球类装备的关联性更为密切。如果我们能将这些有关联的特征找出来,显然是很有意义的。
一般的线性模型为:
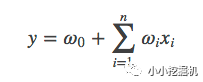
从上面的式子很容易看出,一般的线性模型压根没有考虑特征间的关联。为了表述特征间的相关性,我们采用多项式模型。在多项式模型中,特征xi与xj的组合用xixj表示。为了简单起见,我们讨论二阶多项式模型。具体的模型表达式如下:
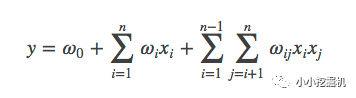
上式中,n表示样本的特征数量,xi表示第i个特征。
与线性模型相比,FM的模型就多了后面特征组合的部分。
4、FM求解
从上面的式子可以很容易看出,组合部分的特征相关参数共有n(n−1)/2个。但是如第二部分所分析,在数据很稀疏的情况下,满足xi,xj都不为0的情况非常少,这样将导致ωij无法通过训练得出。
为了求出ωij,我们对每一个特征分量xi引入辅助向量Vi=(vi1,vi2,⋯,vik)。然后,利用vivj^T对ωij进行求解。
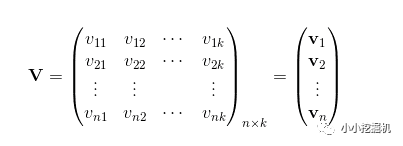
那么ωij组成的矩阵可以表示为:
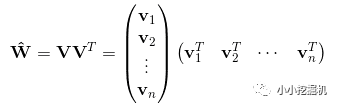
那么,如何求解vi和vj呢?主要采用了公式:
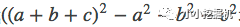
具体过程如下:
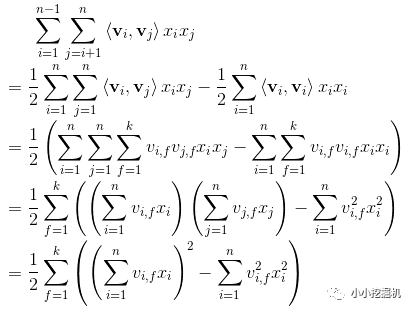
上面的式子中有同学曾经问我第一步是怎么推导的,其实也不难,看下面的手写过程(大伙可不要嫌弃字丑哟)
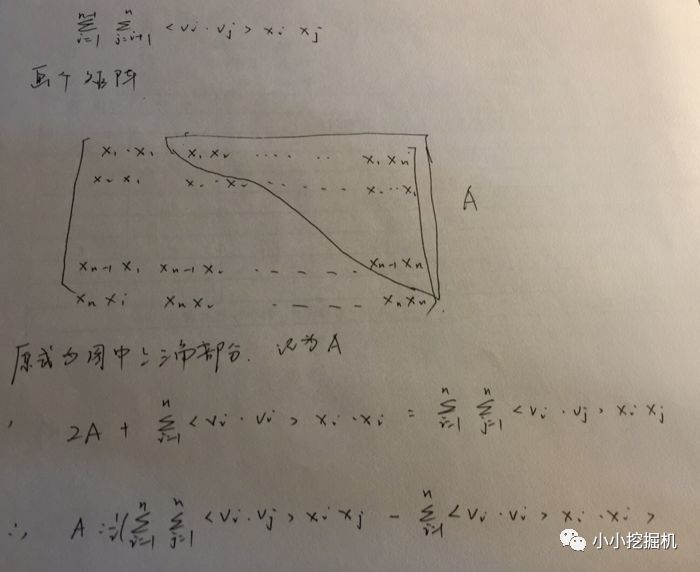
经过这样的分解之后,我们就可以通过随机梯度下降SGD进行求解:
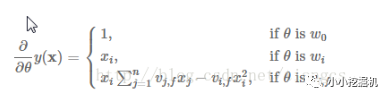
5、tensorflow代码详解
代码参考地址: https://github.com/babakx/fm_tensorflow/blob/master/fm_tensorflow.ipynb
上面的代码使用的是python2编码,在python3下运行会出错,所以如果大家使用的是python3的话,可以参考我写的,其实就是修复了几个bug啦,哈哈。
我的github地址:
https://github.com/princewen/tensorflow_practice/tree/master/recommendation-FM-demo。
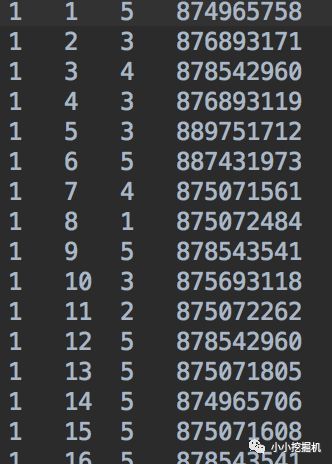
本文使用的数据是MovieLens100k Datase,数据包括四列,分别是用户ID,电影ID,打分,时间。
输入变换
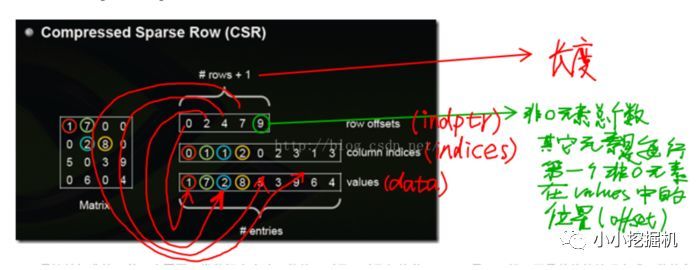
要使用FM模型,我们首先要将数据处理成一个矩阵,矩阵的大小是用户数 * 电影数。如何根据现有的数据进行处理呢?使用的是scipy.sparse中的csr.csr_matrix,理解这个函数真的费了不少功夫呢,不过还是在下面博客( https://blog.csdn.net/u012871493/article/details/51593451)的帮助下理解了函数的原理。盗用博客中的一张图来帮助大家理解这个函数的输入:
函数形式如下:
csr_matrix((data, indices, indptr)
可以看到,函数接收三个参数,第一个参数是数值,第二个参数是每个数对应的列号,第三个参数是每行的起始的偏移量,举上图的例子来说,第0行的起始偏移是0,第0行有2个非0值,因此第一行的起始偏移是2,第1行有两个非0值,因此第二行的起始偏移是4,依次类推。
下面的代码是如何将原始的文件输入转换成我们的矩阵:
def vectorize_dic(dic,ix=None,p=None,n=0,g=0):
"""
dic -- dictionary of feature lists. Keys are the name of features
ix -- index generator (default None)
p -- dimension of featrure space (number of columns in the sparse matrix) (default None)
"""
if ix==None:
ix = dict()
nz = n * g
col_ix = np.empty(nz,dtype = int)
i = 0
for k,lis in dic.items():
for t in range(len(lis)):
ix[str(lis[t]) + str(k)] = ix.get(str(lis[t]) + str(k),0) + 1
col_ix[i+t*g] = ix[str(lis[t]) + str(k)]
i += 1
row_ix = np.repeat(np.arange(0,n),g)
data = np.ones(nz)
if p == None:
p = len(ix)
ixx = np.where(col_ix < p)
return csr.csr_matrix((data[ixx],(row_ix[ixx],col_ix[ixx])),shape=(n,p)),ix
cols = ['user','item','rating','timestamp']
train = pd.read_csv('data/ua.base',delimiter='\t',names = cols)
test = pd.read_csv('data/ua.test',delimiter='\t',names = cols)
x_train,ix = vectorize_dic({'users':train['user'].values,
'items':train['item'].values},n=len(train.index),g=2)
x_test,ix = vectorize_dic({'users':test['user'].values,
'items':test['item'].values},ix,x_train.shape[1],n=len(test.index),g=2)
y_train = train['rating'].values
y_test = test['rating'].values
x_train = x_train.todense()
x_test = x_test.todense()
如果不做处理,函数返回的矩阵是按如下的格式保存的:
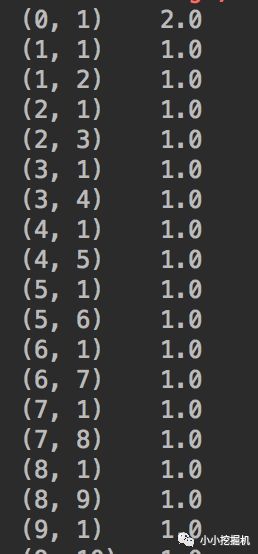
使用todense变换后,变成如下样式:
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/%E4%BA%92%E8%81%94%E7%BD%91/%E6%8E%A8%E8%8D%90%E7%B3%BB%E7%BB%9F%E9%81%87%E4%B8%8A%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0%E4%B8%80%E6%A8%A1%E5%9E%8B%E7%90%86%E8%AE%BA%E5%92%8C%E5%AE%9E%E8%B7%B5/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


