推荐系统遇上深度学习二模型理论和实践
原文发布于微信公众号 - 小小挖掘机(wAIsjwj)
原文发表时间:2018-04-10
1、FFM理论
在CTR预估中,经常会遇到one-hot类型的变量,one-hot类型变量会导致严重的数据特征稀疏的情况,为了解决这一问题,在上一讲中,我们介绍了FM算法。这一讲我们介绍一种在FM基础上发展出来的算法-FFM(Field-aware Factorization Machine)。
FFM模型中引入了类别的概念,即field。还是拿上一讲中的数据来讲,先看下图:
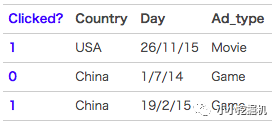
在上面的广告点击案例中,“Day=26/11/15”、“Day=1/7/14”、“Day=19/2/15”这三个特征都是代表日期的,可以放到同一个field中。同理,Country也可以放到一个field中。简单来说,同一个categorical特征经过One-Hot编码生成的数值特征都可以放到同一个field,包括用户国籍,广告类型,日期等等。
在FFM中,每一维特征 xi,针对其它特征的每一种field fj,都会学习一个隐向量 v_i,fj。因此,隐向量不仅与特征相关,也与field相关。也就是说,“Day=26/11/15”这个特征与“Country”特征和“Ad_type"特征进行关联的时候使用不同的隐向量,这与“Country”和“Ad_type”的内在差异相符,也是FFM中“field-aware”的由来。
假设样本的 n个特征属于 f个field,那么FFM的二次项有 nf个隐向量。而在FM模型中,每一维特征的隐向量只有一个。FM可以看作FFM的特例,是把所有特征都归属到一个field时的FFM模型。根据FFM的field敏感特性,可以导出其模型方程。
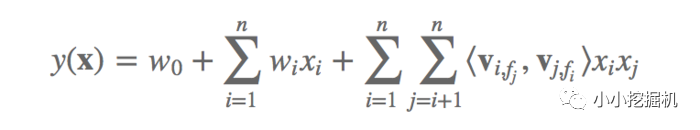
可以看到,如果隐向量的长度为 k,那么FFM的二次参数有 nfk 个,远多于FM模型的 nk个。此外,由于隐向量与field相关,FFM二次项并不能够化简,其预测复杂度是 O(kn^2)。
下面以一个例子简单说明FFM的特征组合方式。输入记录如下:

这条记录可以编码成5个特征,其中“Genre=Comedy”和“Genre=Drama”属于同一个field,“Price”是数值型,不用One-Hot编码转换。为了方便说明FFM的样本格式,我们将所有的特征和对应的field映射成整数编号。
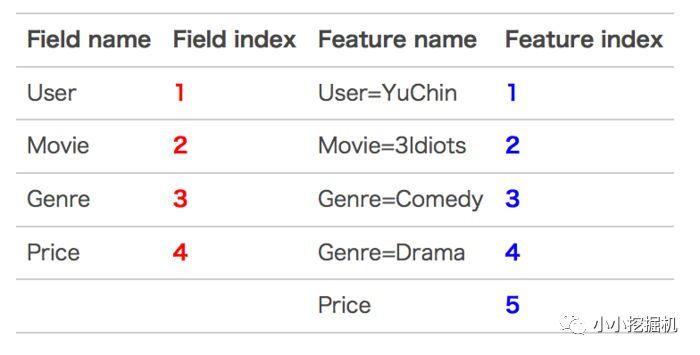
那么,FFM的组合特征有10项,如下图所示。

其中,红色是field编号,蓝色是特征编号。
2、FFM实现细节
这里讲得只是一种FFM的实现方式,并不是唯一的。
损失函数
FFM将问题定义为分类问题,使用的是logistic loss,同时加入了正则项
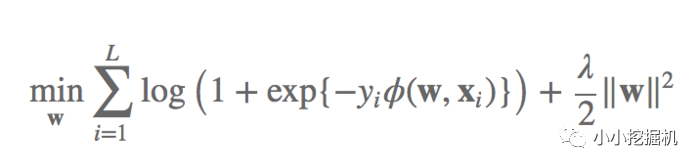
什么,这是logisitc loss?第一眼看到我是懵逼的,逻辑回归的损失函数我很熟悉啊,不是长这样的啊?其实是我目光太短浅了。逻辑回归其实是有两种表述方式的损失函数的,取决于你将类别定义为0和1还是1和-1。大家可以参考下下面的文章: https://www.cnblogs.com/ljygoodgoodstudydaydayup/p/6340129.html。当我们将类别设定为1和-1的时候,逻辑回归的损失函数就是上面的样子。
随机梯度下降
训练FFM使用的是随机梯度下降方法,即每次只选一条数据进行训练,这里还有必要补一补梯度下降的知识,梯度下降是有三种方式的,截图取自参考文献3:

总给人一种怪怪的感觉。batch为什么是全量的数据呢,哈哈。
3、tensorflow实现代码
本文代码的github地址:
https://github.com/princewen/tensorflow_practice/tree/master/recommendation-FFM-Demo
这里我们只讲解一些细节,具体的代码大家可以去github上看:
生成数据
这里我没有找到合适的数据,就自己产生了一点数据,数据涉及20维特征,前十维特征是一个field,后十维是一个field:
def gen_data():
labels = [-1,1]
y = [np.random.choice(labels,1)[0] for _ in range(all_data_size)]
x_field = [i // 10 for i in range(input_x_size)]
x = np.random.randint(0,2,size=(all_data_size,input_x_size))
return x,y,x_field
定义权重项
在ffm中,有三个权重项,首先是bias,然后是一维特征的权重,最后是交叉特征的权重:
def createTwoDimensionWeight(input_x_size,field_size,vector_dimension):
weights = tf.truncated_normal([input_x_size,field_size,vector_dimension])
tf_weights = tf.Variable(weights)
return tf_weights
def createOneDimensionWeight(input_x_size):
weights = tf.truncated_normal([input_x_size])
tf_weights = tf.Variable(weights)
return tf_weights
def createZeroDimensionWeight():
weights = tf.truncated_normal([1])
tf_weights = tf.Variable(weights)
return tf_weights
计算估计值
估计值的计算这里不能项FM一样先将公式化简再来做,对于交叉特征,只能写两重循环,所以对于特别多的特征的情况下,真的计算要爆炸呀!
def inference(input_x,input_x_field,zeroWeights,oneDimWeights,thirdWeight):
"""计算回归模型输出的值"""
secondValue = tf.reduce_sum(tf.multiply(oneDimWeights,input_x,name='secondValue'))
firstTwoValue = tf.add(zeroWeights, secondValue, name="firstTwoValue")
thirdValue = tf.Variable(0.0,dtype=tf.float32)
input_shape = input_x_size
for i in range(input_shape):
featureIndex1 = I
fieldIndex1 = int(input_x_field[I])
for j in range(i+1,input_shape):
featureIndex2 = j
fieldIndex2 = int(input_x_field[j])
vectorLeft = tf.convert_to_tensor([[featureIndex1,fieldIndex2,i] for i in range(vector_dimension)])
weightLeft = tf.gather_nd(thirdWeight,vectorLeft)
weightLeftAfterCut = tf.squeeze(weightLeft)
vectorRight = tf.convert_to_tensor([[featureIndex2,fieldIndex1,i] for i in range(vector_dimension)])
weightRight = tf.gather_nd(thirdWeight,vectorRight)
weightRightAfterCut = tf.squeeze(weightRight)
tempValue = tf.reduce_sum(tf.multiply(weightLeftAfterCut,weightRightAfterCut))
indices2 = [I]
indices3 = [j]
xi = tf.squeeze(tf.gather_nd(input_x, indices2))
xj = tf.squeeze(tf.gather_nd(input_x, indices3))
product = tf.reduce_sum(tf.multiply(xi, xj))
secondItemVal = tf.multiply(tempValue, product)
tf.assign(thirdValue, tf.add(thirdValue, secondItemVal))
return tf.add(firstTwoValue,thirdValue)
定义损失函数
损失函数我们就用逻辑回归损失函数来算,同时加入正则项:
lambda_w = tf.constant(0.001, name='lambda_w')
lambda_v = tf.constant(0.001, name='lambda_v')
zeroWeights = createZeroDimensionWeight()
oneDimWeights = createOneDimensionWeight(input_x_size)
thirdWeight = createTwoDimensionWeight(input_x_size, # 创建二次项的权重变量
field_size,
vector_dimension) # n * f * k
y_ = inference(input_x, trainx_field,zeroWeights,oneDimWeights,thirdWeight)
l2_norm = tf.reduce_sum(
tf.add(
tf.multiply(lambda_w, tf.pow(oneDimWeights, 2)),
tf.reduce_sum(tf.multiply(lambda_v, tf.pow(thirdWeight, 2)),axis=[1,2])
)
)
loss = tf.log(1 + tf.exp(input_y * y_)) + l2_norm
train_step =
- 原文作者:知识铺
- 原文链接:https://geek.zshipu.com/post/%E4%BA%92%E8%81%94%E7%BD%91/%E6%8E%A8%E8%8D%90%E7%B3%BB%E7%BB%9F%E9%81%87%E4%B8%8A%E6%B7%B1%E5%BA%A6%E5%AD%A6%E4%B9%A0%E4%BA%8C%E6%A8%A1%E5%9E%8B%E7%90%86%E8%AE%BA%E5%92%8C%E5%AE%9E%E8%B7%B5/
- 版权声明:本作品采用知识共享署名-非商业性使用-禁止演绎 4.0 国际许可协议进行许可,非商业转载请注明出处(作者,原文链接),商业转载请联系作者获得授权。
- 免责声明:本页面内容均来源于站内编辑发布,部分信息来源互联网,并不意味着本站赞同其观点或者证实其内容的真实性,如涉及版权等问题,请立即联系客服进行更改或删除,保证您的合法权益。转载请注明来源,欢迎对文章中的引用来源进行考证,欢迎指出任何有错误或不够清晰的表达。也可以邮件至 sblig@126.com


