原文地址： https://www.cnblogs.com/wkang/p/9657032.html

1. GBDT + LR 是什么

本质上GBDT+LR是一种具有stacking思想的二分类器模型，所以可以用来解决二分类问题。这个方法出自于Facebook 2014年的论文 Practical Lessons from Predicting Clicks on Ads at Facebook 。

2. GBDT + LR 用在哪

GBDT+LR 使用最广泛的场景是CTR点击率预估，即预测当给用户推送的广告会不会被用户点击。

点击率预估模型涉及的训练样本一般是上亿级别，样本量大，模型常采用速度较快的LR。但LR是线性模型，学习能力有限，此时特征工程尤其重要。现有的特征工程实验，主要集中在寻找到有区分度的特征、特征组合，折腾一圈未必会带来效果提升。GBDT算法的特点正好可以用来发掘有区分度的特征、特征组合，减少特征工程中人力成本。

从知乎 https://zhuanlan.zhihu.com/p/29053940 上看到了一个关于CTR的流程，如下图所示：

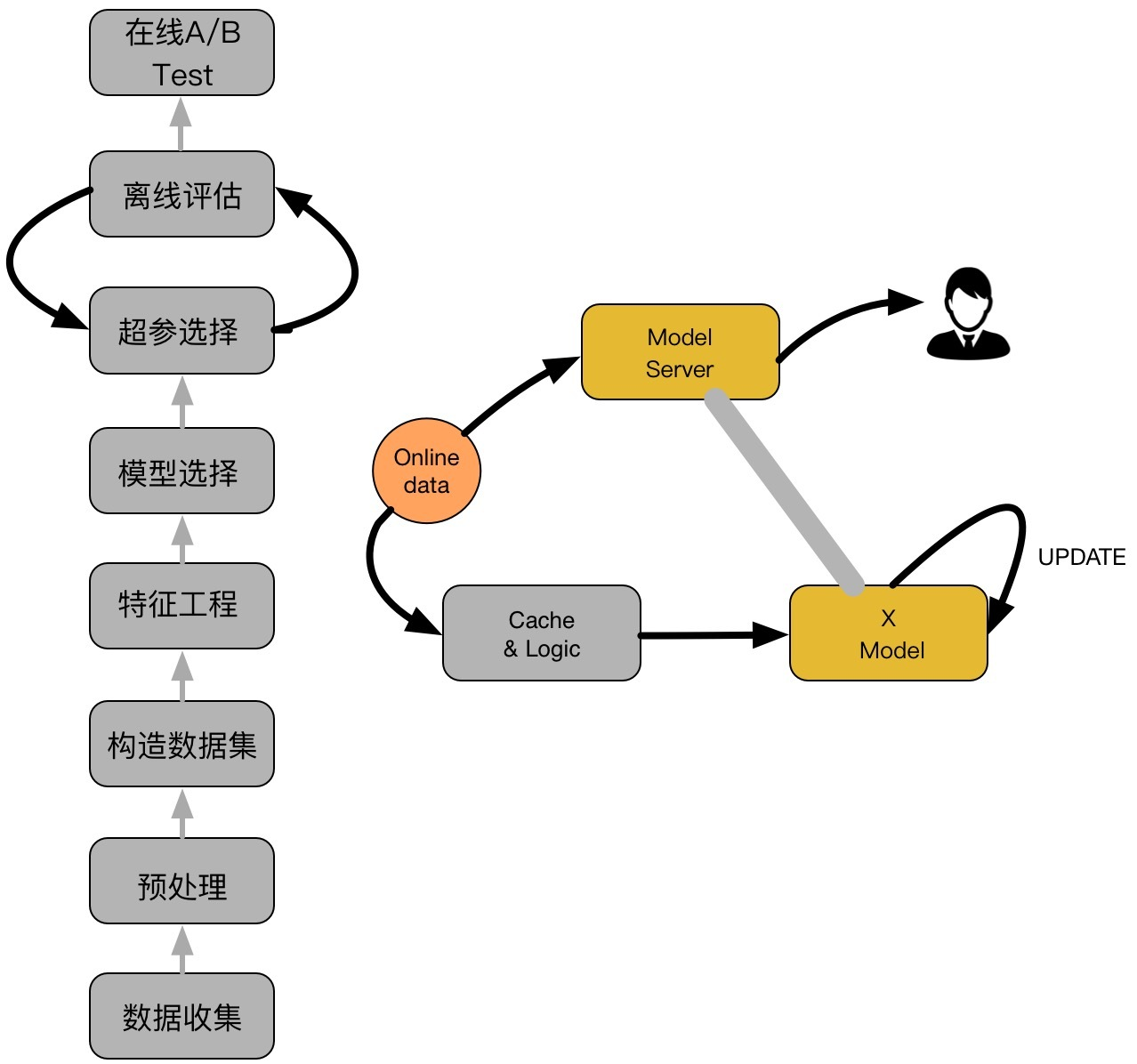
如上图，主要包括两大部分：离线部分、在线部分，其中离线部分目标主要是训练出可用模型，而在线部分则考虑模型上线后，性能可能随时间而出现下降，弱出现这种情况，可选择使用Online-Learning来在线更新模型：

2.1 离线部分

数据收集：主要收集和业务相关的数据，通常会有专门的同事在app位置进行埋点，拿到业务数据
预处理：对埋点拿到的业务数据进行去脏去重；
构造数据集：经过预处理的业务数据，构造数据集，在切分训练、测试、验证集时应该合理根据业务逻辑来进行切分；
特征工程：对原始数据进行基本的特征处理，包括去除相关性大的特征，离散变量one-hot，连续特征离散化等等;
模型选择：选择合理的机器学习模型来完成相应工作，原则是先从简入深，先找到baseline，然后逐步优化；
超参选择：利用gridsearch、randomsearch或者hyperopt来进行超参选择，选择在离线数据集中性能最好的超参组合；
在线A/B Test：选择优化过后的模型和原先模型（如baseline）进行A/B Test，若性能有提升则替换原先模型；

2.2 在线部分

Cache & Logic：设定简单过滤规则，过滤异常数据；
模型更新：当Cache & Logic 收集到合适大小数据时，对模型进行pretrain+finetuning，若在测试集上比原始模型性能高，则更新model server的模型参数；
Model Server：接受数据请求，返回预测结果；

3. GBDT + LR 的结构

正如它的名字一样，GBDT+LR 由两部分组成，其中GBDT用来对训练集提取特征作为新的训练输入数据，LR作为新训练输入数据的分类器。

具体来讲，有以下几个步骤：

3.1 GBDT首先对原始训练数据做训练，得到一个二分类器，当然这里也需要利用网格搜索寻找最佳参数组合。

3.2 与通常做法不同的是，当GBDT训练好做预测的时候，输出的并不是最终的二分类概率值，而是要把模型中的每棵树计算得到的预测概率值所属的叶子结点位置记为1，这样，就构造出了新的训练数据。

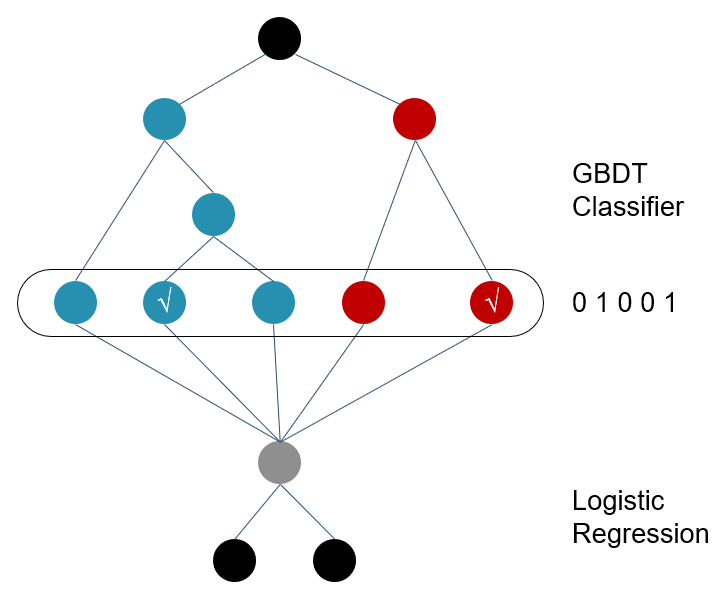
举个例子，下图是一个GBDT+LR 模型结构，设GBDT有两个弱分类器，分别以蓝色和红色部分表示，其中蓝色弱分类器的叶子结点个数为3，红色弱分类器的叶子结点个数为2，并且蓝色弱分类器中对0-1 的预测结果落到了第二个叶子结点上，红色弱分类器中对0-1 的预测结果也落到了第二个叶子结点上。那么我们就记蓝色弱分类器的预测结果为[0 1 0]，红色弱分类器的预测结果为[0 1]，综合起来看，GBDT的输出为这些弱分类器的组合[0 1 0 0 1] ，或者一个稀疏向量（数组）。

这里的思想与One-hot独热编码类似，事实上，在用GBDT构造新的训练数据时，采用的也正是One-hot方法。并且由于每一弱分类器有且只有一个叶子节点输出预测结果，所以在一个具有n个弱分类器、共计m个叶子结点的GBDT中，每一条训练数据都会被转换为1*m维稀疏向量，且有n个元素为1，其余m-n 个元素全为0。

3.3 新的训练数据构造完成后，下一步就要与原始的训练数据中的label(输出)数据一并输入到Logistic Regression分类器中进行最终分类器的训练。思考一下，在对原始数据进行GBDT提取为新的数据这一操作之后，数据不仅变得稀疏，而且由于弱分类器个数，叶子结点个数的影响，可能会导致新的训练数据特征维度过大的问题，因此，在Logistic Regression这一层中，可使用正则化来减少过拟合的风险，在Facebook的论文中采用的是L1正则化。

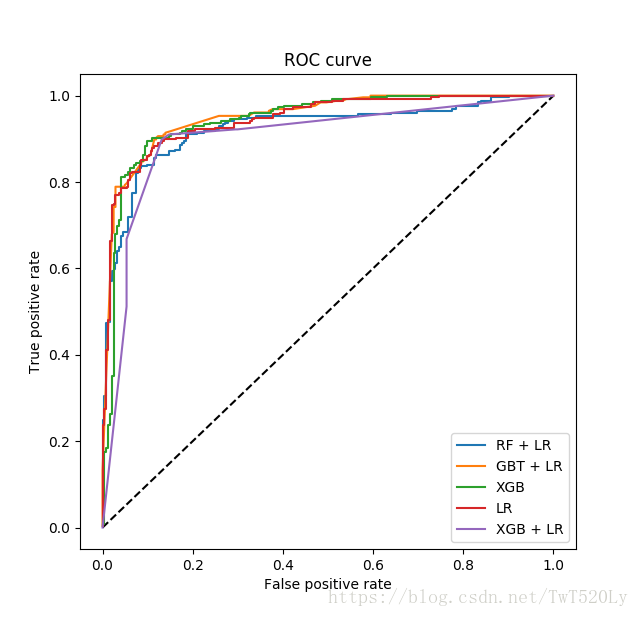
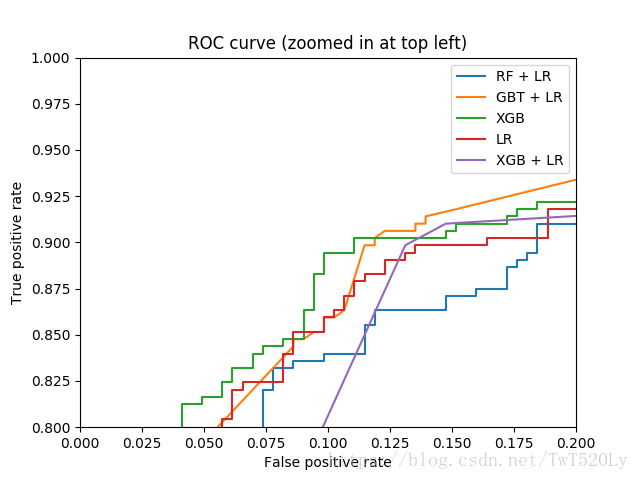
4. RF + LR ? Xgb + LR?

有心的同学应该会思考一个问题，既然GBDT可以做新训练样本的构造，那么其它基于树的模型，例如Random Forest以及Xgboost等是并不是也可以按类似的方式来构造新的训练样本呢？没错，所有这些基于树的模型都可以和Logistic Regression分类器组合。至于效果孰优孰劣，我个人觉得效果都还可以，但是之间没有可比性，因为超参数的不同会对模型评估产生较大的影响。下图是RF+LR、GBT+LR、Xgb、LR、Xgb+LR 模型效果对比图，然而这只能做个参考，因为模型超参数的值的选择这一前提条件都各不相同。

顺便来讲，RF也是多棵树，但从效果上有实践证明不如GBDT。且GBDT前面的树，特征分裂主要体现对多数样本有区分度的特征；后面的树，主要体现的是经过前N颗树，残差仍然较大的少数样本。优先选用在整体上有区分度的特征，再选用针对少数样本有区分度的特征，思路更加合理，这应该也是用GBDT的原因。

5. GBDT + LR 代码分析

在网上找到了两个版本的GBDT+LR的代码实现，通过阅读分析，认为里面有一些细节还是值得好好学习一番的，所以接下来这一小节会针对代码实现部分做一些总结。

首先，目前我所了解到的GBDT的实现方式有两种：一是利用Scikit-learn中的ensemble.GradientBoostingClassifier ，二是利用lgb里的params={ ‘boosting_type’: ‘gbdt’ }参数。接下里分别对这两种实现方式进行分析。

5.1 Scikit-learn的实现：

from sklearn.preprocessing import OneHotEncoder
from sklearn.ensemble import GradientBoostingClassifier

gbm1 = GradientBoostingClassifier(n_estimators=50, random_state=10, subsample=0.6, max_depth=7,
                                  min_samples_split=900)
gbm1.fit(X_train, Y_train)
train_new_feature = gbm1.apply(X_train)
train_new_feature = train_new_feature.reshape(-1, 50)

enc = OneHotEncoder()

enc.fit(train_new_feature)

# # 每一个属性的最大取值数目
# print('每一个特征的最大取值数目:', enc.n_values_)
# print('所有特征的取值数目总和:', enc.n_values_.sum())

train_new_feature2 = np.array(enc.transform(train_new_feature).toarray())

划重点：

5.1.1 model.apply(X_train)的用法

model.apply(X_train)返回训练数据X_train在训练好的模型里每棵树中所处的叶子节点的位置（索引）

5.1.2 sklearn.preprocessing 中OneHotEncoder的使用

除了pandas中的 get_dummies()，sklearn也提供了一种对Dataframe做One-hot的方法。

OneHotEncoder() 首先fit() 过待转换的数据后，再次transform() 待转换的数据，就可实现对这些数据的所有特征进行One-hot 操作。

由于transform() 后的数据格式不能直接使用，所以最后需要使用.toarray() 将其转换为我们能够使用的数组结构。

enc.transform(train_new_feature).toarray()

5.1.3 sklearn中的GBDT 能够设置树的个数，每棵树最大叶子节点个数等超参数，但不能指定每颗树的叶子节点数。

5.2 lightgbm 的实现

params = {
    'task': 'train',
    'boosting_type': 'gbdt',
    'objective': 'binary',
    'metric': {'binary_logloss'},
    'num_leaves': 64,
    'num_trees': 100,
    'learning_rate': 0.01,
    'feature_fraction': 0.9,
    'bagging_fraction': 0.8,
    'bagging_freq': 5,
    'verbose': 0
}

# number of leaves,will be used in feature transformation
num_leaf = 64

print('Start training...')
# train
gbm = lgb.train(params=params,
                train_set=lgb_train,
                valid_sets=lgb_train, )

print('Start predicting...')
# y_pred分别落在100棵树上的哪个节点上
y_pred = gbm.predict(x_train, pred_leaf=True)
y_pred_prob = gbm.predict(x_train)

result = []
threshold = 0.5
for pred in y_pred_prob:
    result.append(1 if pred > threshold else 0)
print('result:', result)

print('Writing transformed training data')
transformed_training_matrix = np.zeros([len(y_pred), len(y_pred[1]) * num_leaf],
                                       dtype=np.int64)  # N * num_tress * num_leafs
for i in range(0, len(y_pred)):
    # temp表示在每棵树上预测的值所在节点的序号（0,64,128,...,6436 为100棵树的序号，中间的值为对应树的节点序号）
    temp = np.arange(len(y_pred[0])) * num_leaf + np.array(y_pred[i])
    # 构造one-hot 训练数据集
    transformed_training_matrix[i][temp] += 1

y_pred = gbm.predict(x_test, pred_leaf=True)
print('Writing transformed testing data')
transformed_testing_matrix = np.zeros([len(y_pred), len(y_pred[1]) * num_leaf], dtype=np.int64)
for i in range(0, len(y_pred)):
    temp = np.arange(len(y_pred[0])) * num_leaf + np.array(y_pred[i])
    # 构造one-hot 测试数据集
    transformed_testing_matrix[i][temp] += 1

划重点：

5.2.1 params 字典里超参数的设置

因为是二分类问题，所以设置 {‘boosting_type’: ‘gbdt’,‘objective’: ‘binary’,‘metric’: {‘binary_logloss’}}，然后设置树的个数及每棵树的叶子结点个数{’num_leaves’: 64,’num_trees’: 100}

5.2.2 model.predict(x_train, pred_leaf=True)

使用

model.predict(x_train, pred_leaf=True)

返回训练数据在训练好的模型里预测结果所在的每棵树中叶子节点的位置（索引），形式为7999*100的二维数组。

5.2.3 构造Ont-hot数组作为新的训练数据

这里并没有使用sklearn中的OneHotEncoder()，也没有使用pandas中的get_dummies()，而是手工创建一个One-hot数组。(当然也可以像5.1.2 那样操作)

首先，创建一个二维零数组用于存放one-hot的元素；
然后，获取第2步得到的二维数组里每个叶子节点在整个GBDT模型里的索引号，因为一共有100棵树，每棵树有64个叶子节点，所以索引范围是0~6400；（这里有一个技巧，通过把每棵树的起点索引组成一个列表，再加上由落在每棵树叶子节点的索引组成的列表，就得到了往二维零数组里插入元素的索引信息）
最后，

temp = np.arange(len(y_pred[0])) * num_leaf + np.array(y_pred[i])

5.2.4 对二维数组填充信息，采用"+=" 的方法

构造one-hot 训练数据集

transformed_training_matrix[i][temp] += 1

6. GBDT + LR 模型提升

现在，我们思考这样一个问题，Logistic Regression是一个线性分类器，也就是说会忽略掉特征与特征之间的关联信息，那么是否可以采用构建新的交叉特征这一特征组合方式从而提高模型的

文章目录

算法解析及实现

1. GBDT + LR 是什么

2. GBDT + LR 用在哪

2.1 离线部分

2.2 在线部分

3. GBDT + LR 的结构

4. RF + LR ? Xgb + LR?

5. GBDT + LR 代码分析

5.1 Scikit-learn的实现：

划重点：

5.1.1 model.apply(X_train)的用法

5.1.2 sklearn.preprocessing 中OneHotEncoder的使用

5.1.3 sklearn中的GBDT 能够设置树的个数，每棵树最大叶子节点个数等超参数，但不能指定每颗树的叶子节点数。

5.2 lightgbm 的实现

划重点：

5.2.1 params 字典里超参数的设置

5.2.2 model.predict(x_train, pred_leaf=True)

5.2.3 构造Ont-hot数组作为新的训练数据

5.2.4 对二维数组填充信息，采用"+=" 的方法

构造one-hot 训练数据集

6. GBDT + LR 模型提升

See Also

最近文章

福利派送

分类

标签

友情链接

其它